Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д.

ЦЕЛИ:
Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса.
Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в зависимости от k и b.
Применить полученные знания при построении графиков кусочной функции.

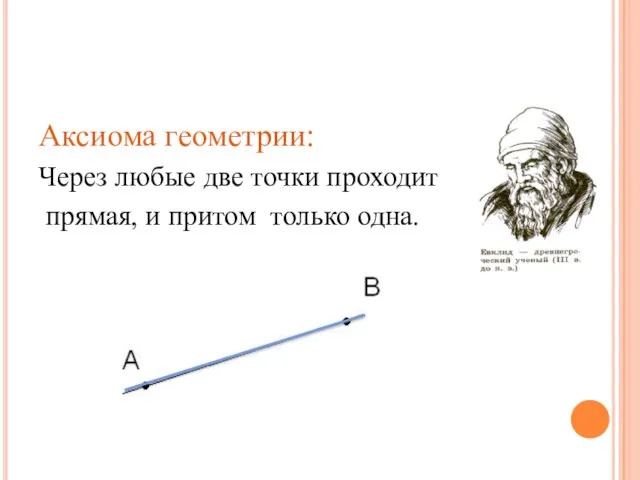
Аксиома геометрии:
Через любые две точки проходит
прямая, и притом только одна.

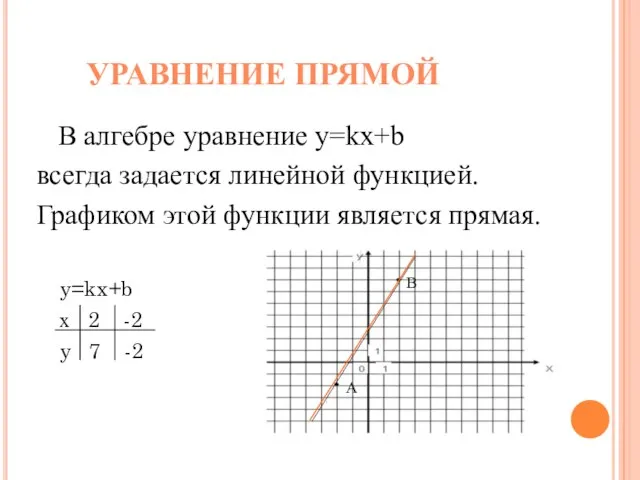
УРАВНЕНИЕ ПРЯМОЙ
В алгебре уравнение y=kx+b
всегда задается линейной функцией.
Графиком этой функции является прямая.
y=kx+b
х 2 -2
y 7 -2
В
А

ПАРАЛЛЕЛЬНЫЕ И ПЕРЕСЕКАЮЩИЕСЯ
ПРЯМЫЕ
В геометрии на плоскости прямые а и b могут быть пересекающимися (рис.1) или параллельными (рис.2).
Пересекающиеся прямые-
это прямые, которые
пересекаются в одной точке.
Параллельные прямые-
это прямые, которые не
пересекаются .
а
а
b
b
рис . 1
рис. 2

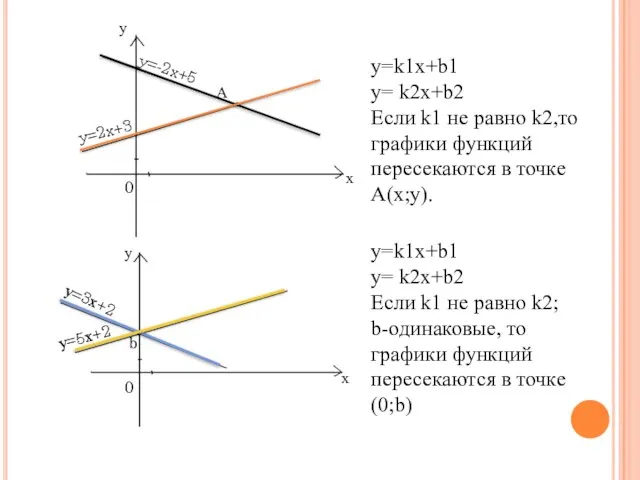
y=k1x+b1
y= k2x+b2
Если k1 не равно k2,то графики функций пересекаются в точке A(x;y).
х
у
у
х
0
y=k1x+b1
y= k2x+b2
Если k1 не равно k2;
b-одинаковые, то графики функций пересекаются в точке (0;b)

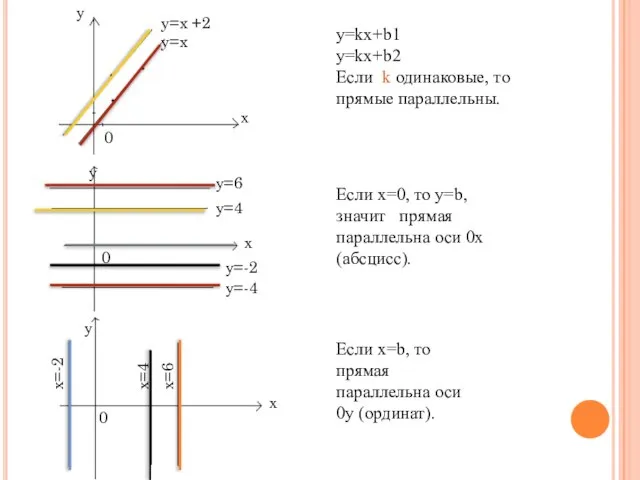
y=x +2
y=x
y=kx+b1
y=kx+b2
Если k одинаковые, то прямые параллельны.
Если х=0, то y=b, значит прямая параллельна оси 0x (абсцисс).
Если x=b, то прямая параллельна оси 0y (ординат).
0
0
0
х
х
х
у
у
у
у=6
у=4
у=-2
у=-4
х=-2
х=4
х=6