Содержание
- 2. ПОВТОРЕНИЕ К ГИА http://79.174.69.4/os/xmodules/qprint/afrms.php?proj Углы в треугольниках
- 3. № 035C64 Ответ: 8. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
- 4. № 0E7DE6 Ответ: 75. В окружности с центром в точке О проведены диаметры AD и BC,
- 5. ПОВТОРЕНИЕ К ГИА http://79.174.69.4/os/xmodules/qprint/afrms.php?proj Центральные и вписанные углы
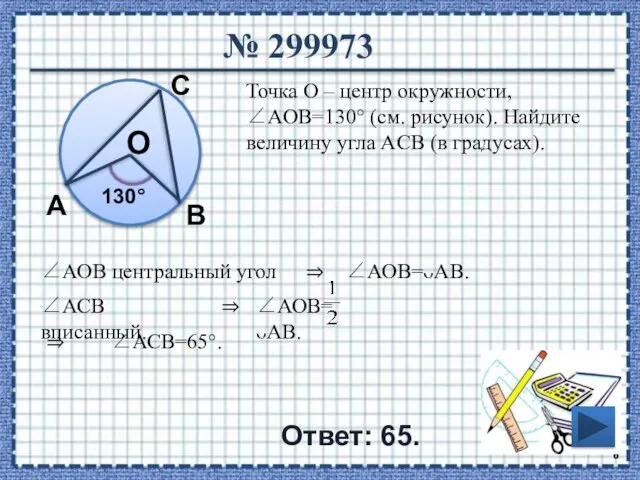
- 6. № 299973 Ответ: 65. Точка О – центр окружности, ∠AOB=130° (см. рисунок). Найдите величину угла ACB
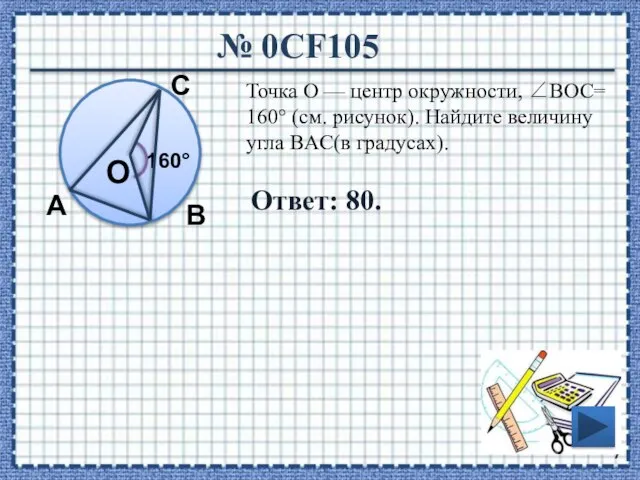
- 7. № 0CF105 Ответ: 80. Точка О — центр окружности, ∠BOC= 160° (см. рисунок). Найдите величину угла
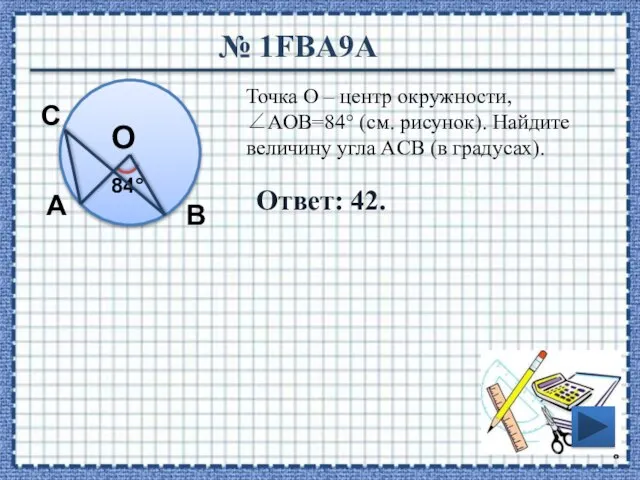
- 8. № 1FBA9A Ответ: 42. Точка О – центр окружности, ∠AOB=84° (см. рисунок). Найдите величину угла ACB
- 9. ПОВТОРЕНИЕ К ГИА http://79.174.69.4/os/xmodules/qprint/afrms.php?proj Касательные к окружности
- 10. № C55047 Ответ: 20. Найдите угол АСО, если его сторона СА касается окружности, О—центр окружности, а
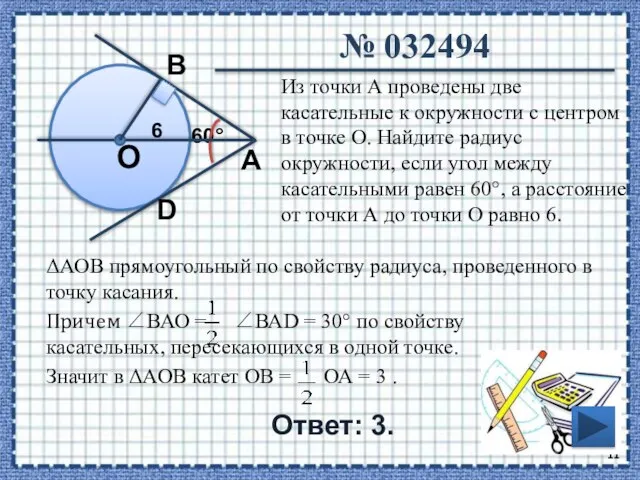
- 11. № 032494 Ответ: 3. Из точки А проведены две касательные к окружности с центром в точке
- 13. Скачать презентацию






 Теорема о вписанном угле 8 класс - презентация_
Теорема о вписанном угле 8 класс - презентация_ Аксиомы стереометрии Решение задач
Аксиомы стереометрии Решение задач От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Многообразие многоугольников
Многообразие многоугольников Золотое сечение или гармоническая пропорция
Золотое сечение или гармоническая пропорция Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии Геометрия. Как она возникла?
Геометрия. Как она возникла? Плоскость
Плоскость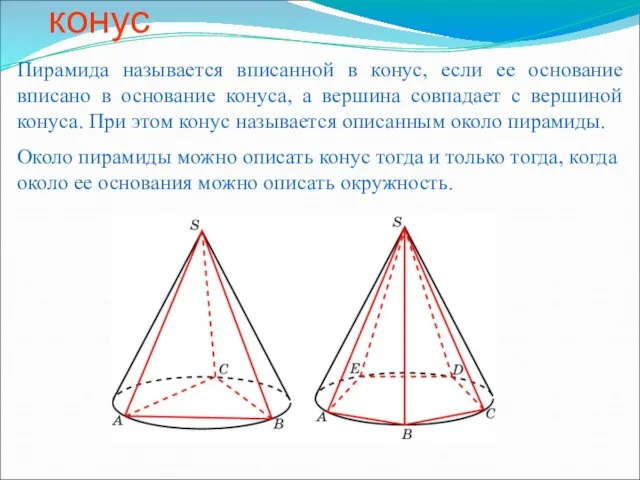 Пирамида, вписанная в конус
Пирамида, вписанная в конус Презентация на тему: Сечение
Презентация на тему: Сечение Урок повторения в 6 классе
Урок повторения в 6 классе Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Окружность в аксонометрии
Окружность в аксонометрии Упражнения со спичками (занятие 9)
Упражнения со спичками (занятие 9) Амидекстр
Амидекстр Длина окружности
Длина окружности Площади и объемы
Площади и объемы Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ Виды углов. Измерение углов
Виды углов. Измерение углов Сфера
Сфера Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Многогранники
Многогранники Двугранный угол. Признак перпендикулярности двух плоскостей
Двугранный угол. Признак перпендикулярности двух плоскостей Путешествие в страну Геометрия
Путешествие в страну Геометрия Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Резьба. Крепёжные изделия
Резьба. Крепёжные изделия