Содержание
- 2. Содержание: 1 Введение 2 Что такое вектор? 3 Равенство, коллинеарность, противоположность и одинаковость направления векторов 4
- 3. 1. Введение. Кто не знает, в какую гавань он плывёт, для того нет попутного ветра Сенека
- 4. Рассмотреть его положения и научится хорошо разбирать и решать задачи, показать основные аспекты связанные с вектором.
- 5. 2. Что такое вектор? Одним из фундаментальных понятий современной математики являются вектор и его обобщение –
- 6. Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы
- 7. Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные
- 8. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный
- 9. Однако это определение, несмотря на его полную конкретность, нас здесь так же не сможет удовлетворить, так
- 10. 3. Равенство, коллинеарность, противоположность и одинаковость направления векторов Два вектора называются равными если они сонаправленны и
- 11. 4. Операции над векторами Так же с векторами можно производить различные операции: Складывать (по правилу треугольника,
- 12. 5.Векторы в пространстве. Высь, ширь, глубь, Лишь, три координаты. Мимо них, где путь? Засов закрыт… (В.
- 13. Множества всех плоских и пространственных векторов, для которых определены операции сложения и умножения, а также умножения
- 14. Оси координат обозначаются так: Ох, Оу, Оz – и имеют названия: ось абсцисс, ось ординат, ось
- 15. 6. Скалярное произведение векторов Зная, как выполняется сложение векторов и умножение вектора на число. Введём ещё
- 16. 7. Векторный метод решения задач Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось и
- 17. Основные компоненты векторного метода решения задач. 1. Перевод условия задачи на язык векторов: - выбор системы
- 18. 8. Заключение Геометрия приближает разум к истине Платон Мастерство- это то, чего нужно добиться А.С. Макаренко.
- 19. 9. Список используемой литературы Автор,Название 1.В.А. Гусев, Ю.М. Колягин, Г.Л. Луканин.«Векторы в школьном курсе геометрии» (1976г.)
- 21. Скачать презентацию


















 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием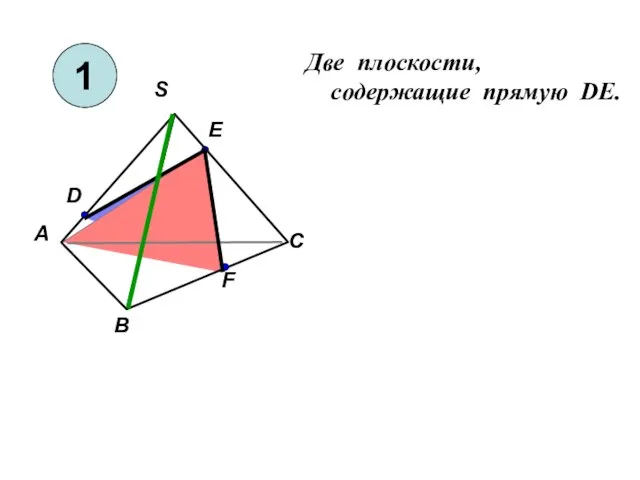 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия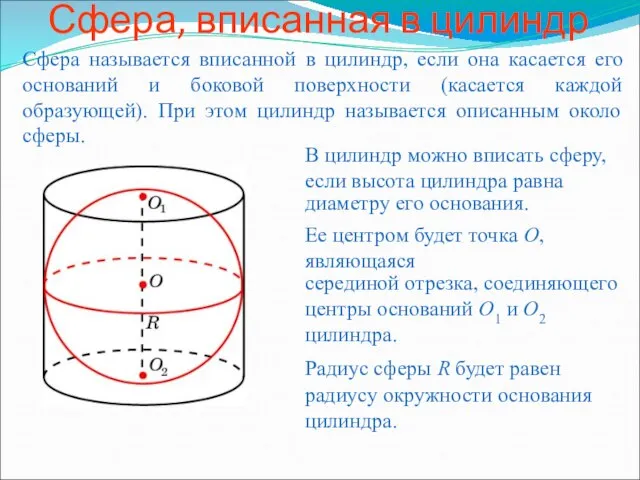 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты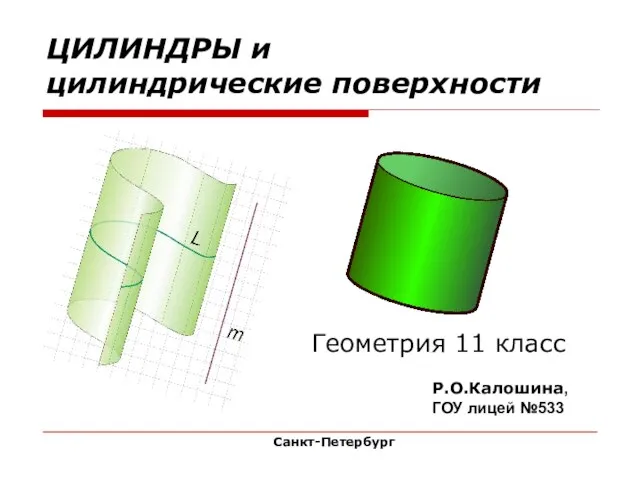 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика