Содержание
- 2. 1. Что означают слова «решение треугольника»? Решением треугольника называется нахождение неизвестных сторон и углов треугольника по
- 3. Сформулируйте теорему синусов. Стороны треугольника пропорциональны синусам противолежащих углов
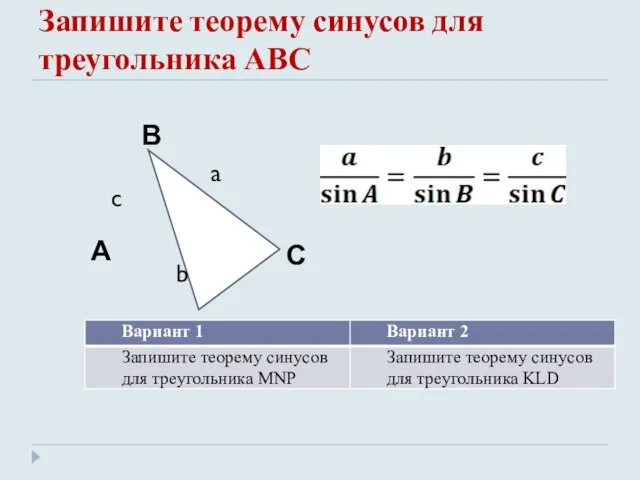
- 4. Запишите теорему синусов для треугольника АВС
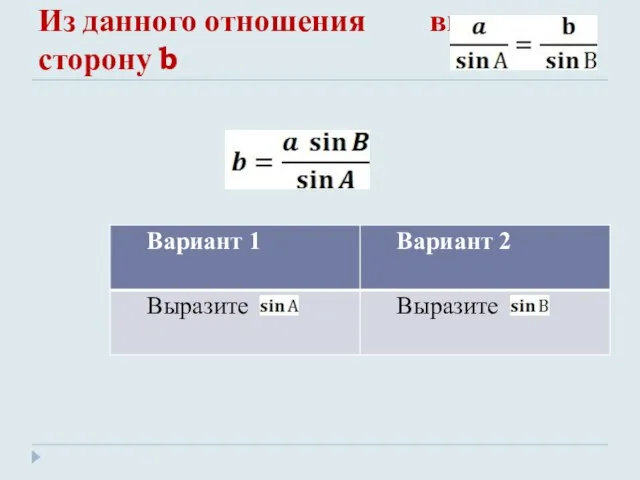
- 5. Из данного отношения выразите сторону b
- 6. Сформулируйте теорему косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих
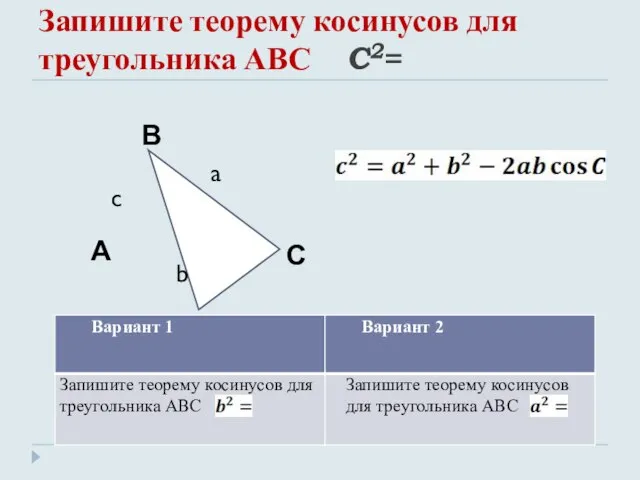
- 7. Запишите теорему косинусов для треугольника АВС C2=
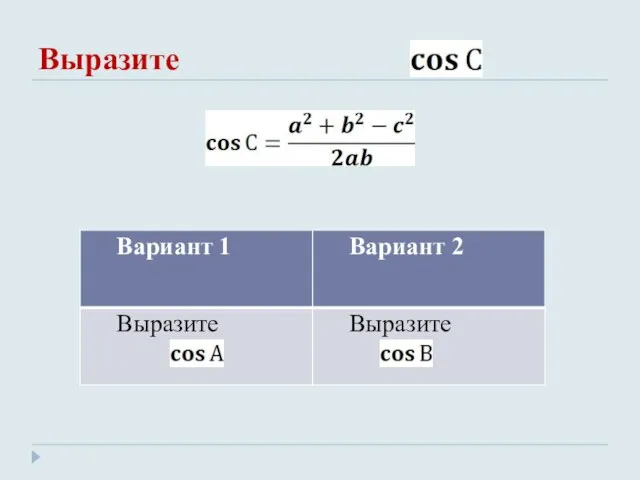
- 8. Выразите
- 9. Сформулируйте основные задачи на решение треугольников По двум сторонам и углу между ними. По стороне и
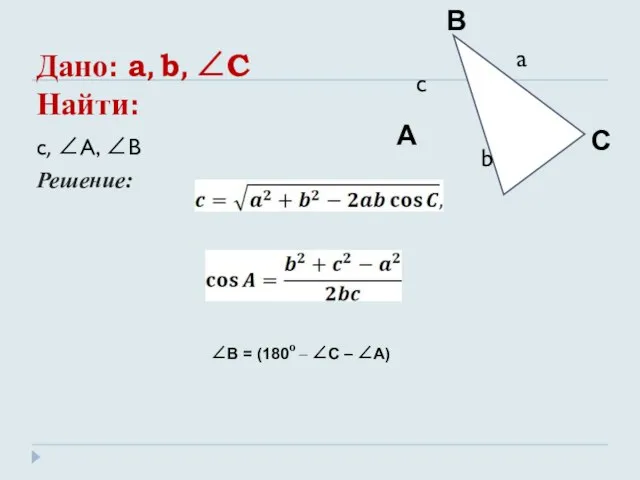
- 10. Дано: a, b, ∠C Найти: c, ∠A, ∠B Решение: ∠B = (180º – ∠C – ∠A)
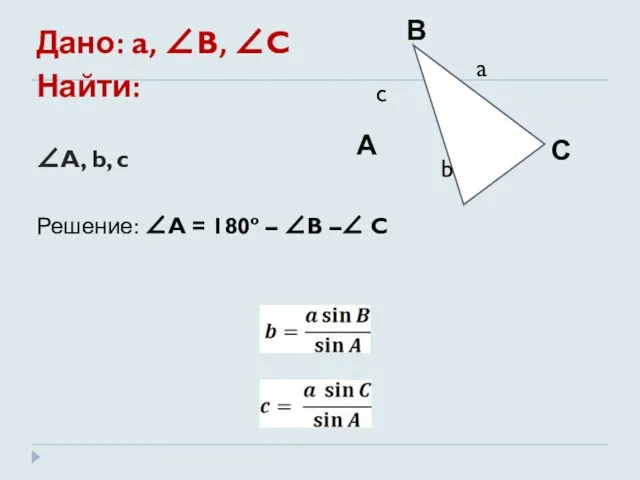
- 11. Дано: a, ∠B, ∠C Найти: ∠A, b, c Решение: ∠A = 180º – ∠B –∠ C
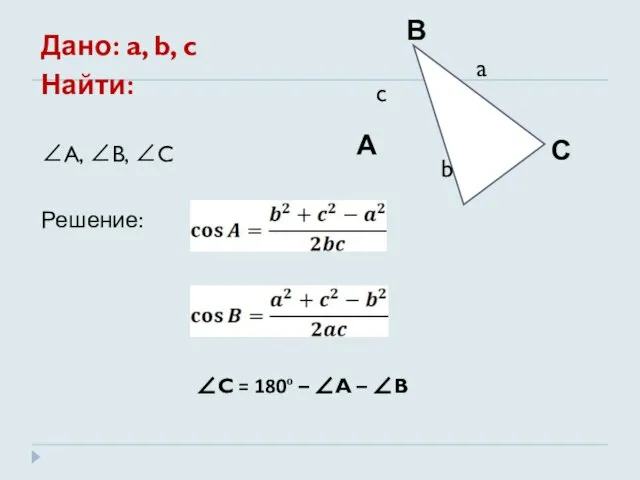
- 12. Дано: a, b, c Найти: ∠A, ∠B, ∠C Решение: ∠C = 180º – ∠A – ∠B
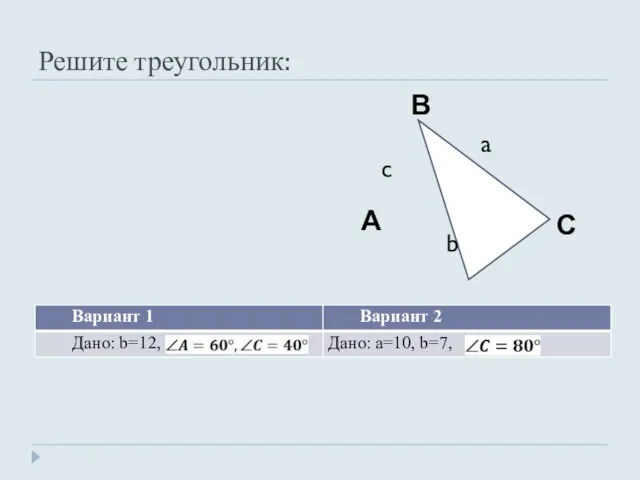
- 13. Решите треугольник:
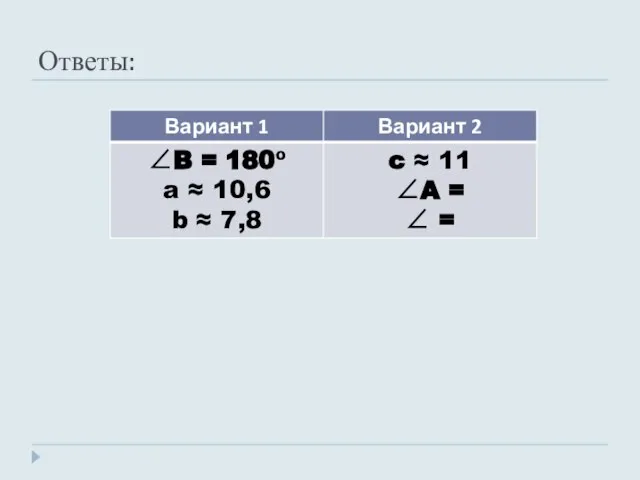
- 14. Ответы:
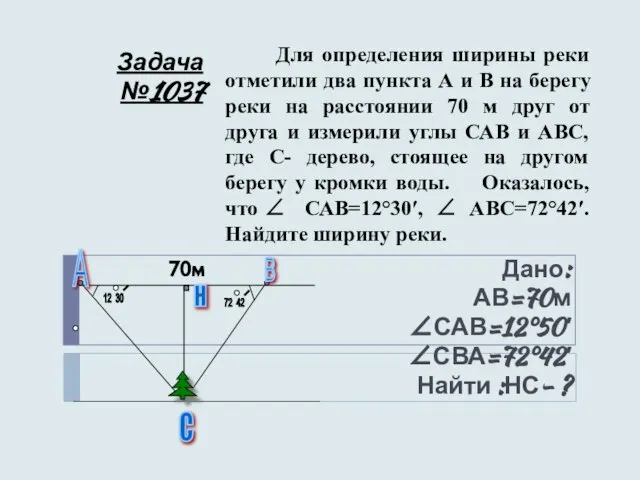
- 15. Задача №1037 Дано: АВ=70м ∠САВ=12°50′ ∠СВА=72°42′ Найти :НС- ? Для определения ширины реки отметили два пункта
- 16. Задача №1038 На горе находится башня, высота которой равна 100м. Некоторый предмет А у подножья горы
- 17. Радиолокация (от лат radio – испускаю лучи и location - расположение) - область науки и техники,
- 18. в военном деле (ПВО, точность стрельбы); в морской, воздушной и космической навигации; в сейсмологии; в метеорологии;
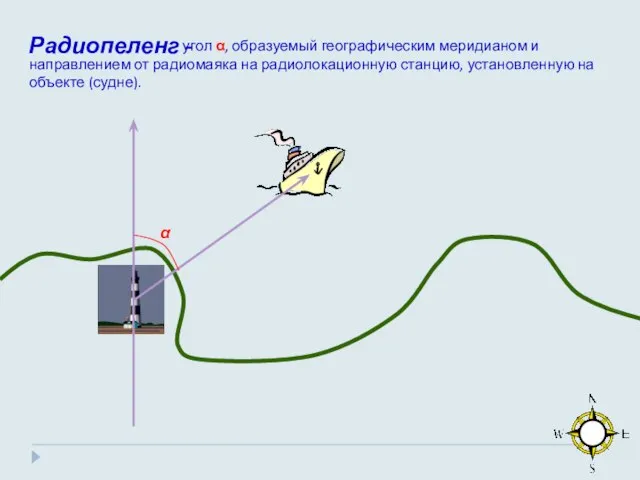
- 19. угол α, образуемый географическим меридианом и направлением от радиомаяка на радиолокационную станцию, установленную на объекте (судне).
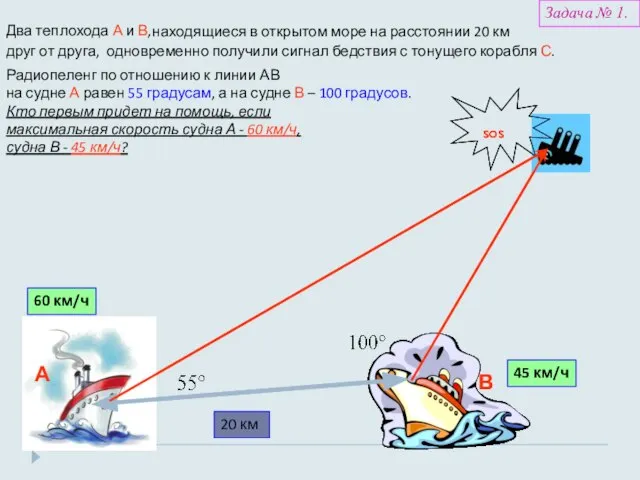
- 20. Плавание на объект радиопеленгования Задача № 1
- 21. Два теплохода А и В, находящиеся в открытом море на расстоянии 20 км 20 км друг
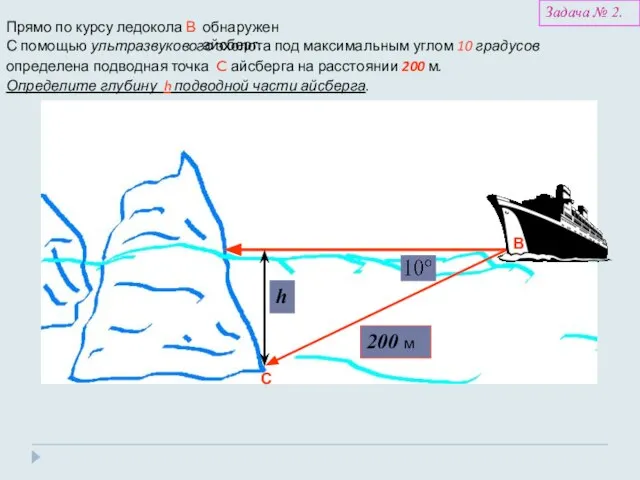
- 22. Определение глубины подводной части объекта средствами гидроакустики Задача № 2
- 23. Прямо по курсу ледокола В обнаружен айсберг. С помощью ультразвукового эхолота под максимальным углом 10 градусов
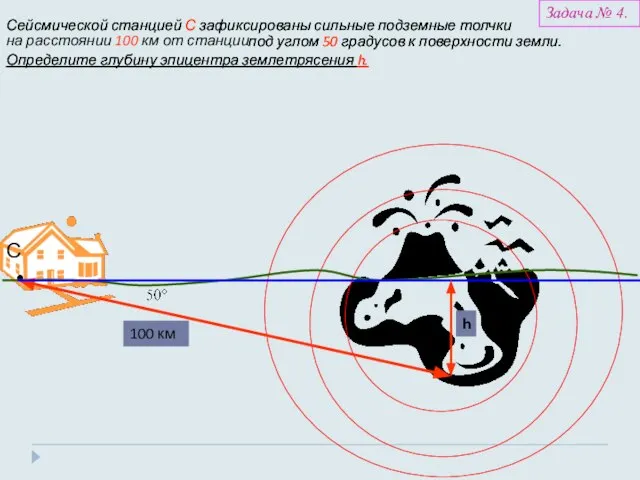
- 24. Определение эпицентра землетрясения Задача № 3
- 25. Сейсмической станцией С зафиксированы сильные подземные толчки С на расстоянии 100 км от станции 100 км
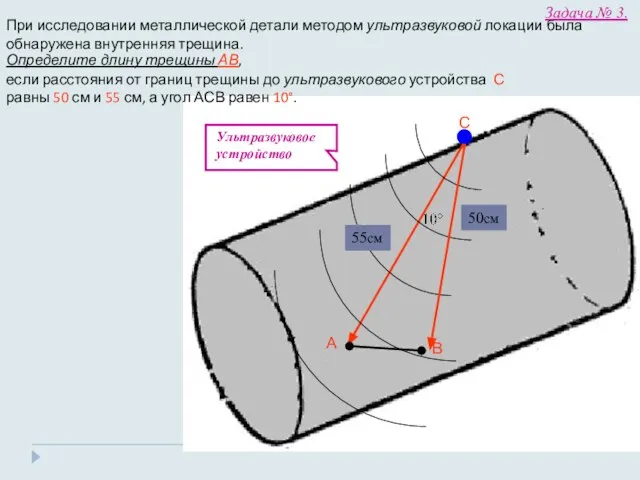
- 26. Определение размеров дефекта внутри металлической детали большой толщины Задача № 4
- 27. А При исследовании металлической детали методом ультразвуковой локации была обнаружена внутренняя трещина. В Определите длину трещины
- 29. Скачать презентацию











 Многогранники
Многогранники Четырехугольники
Четырехугольники Пентагон
Пентагон Площади фигур. Зачёт
Площади фигур. Зачёт Первый признак равенства треугольников
Первый признак равенства треугольников Теорема косинусов
Теорема косинусов Правильные многоугольники (9 класс)
Правильные многоугольники (9 класс) Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Луч и угол (7 класс)
Луч и угол (7 класс) Объём призмы
Объём призмы Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска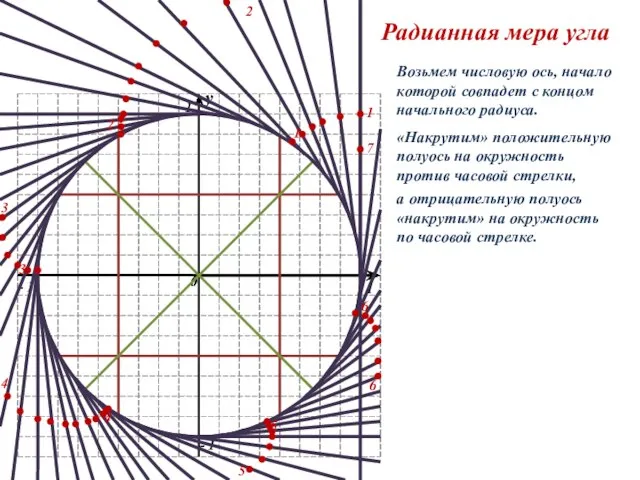 Радианная мера угла
Радианная мера угла Карточки - задания по теме "Конус"
Карточки - задания по теме "Конус" «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Почему квадрат?
Почему квадрат? Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Проецирование (8 класс)
Проецирование (8 класс) Биссектриса угла
Биссектриса угла Параллельные прямые
Параллельные прямые Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Чудеса симметрии
Чудеса симметрии Длина отрезка
Длина отрезка Скалярное произведение векторов
Скалярное произведение векторов