Слайд 2Содержание
Сферическая поверхность
Уравнение сферы
Взаимное расположение сферы и плоскости
Касательная плоскость к сфере
Площадь сферы,

объем шара
Вопросы
Слайд 3Сферическая поверхность
Сферической поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки

– центра.
Тело, ограниченное сферической поверхностью, называется шаром.
Слайд 4Сферическая поверхность
(продолжение)
O – центр сферы
R – радиус сферы
Ось – любая прямая, проходящая

через центр сферы
Слайд 5Уравнение сферы
В прямоугольной системе координат уравнение сферы радиуса R
с центром C

(xo;yo;zo) имеет вид:
(x-xo)²+(y-yo)²+(z-zo)²=R²
Слайд 6Взаимное расположение сферы и плоскости
Если расстояние от центра сферы до плоскости меньше
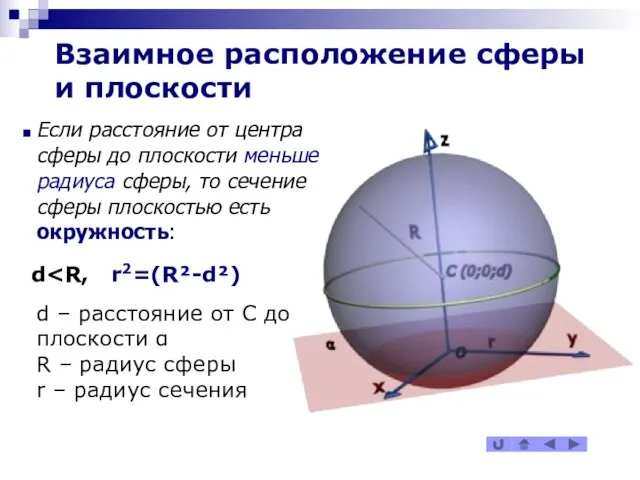
радиуса сферы, то сечение сферы плоскостью есть окружность:
d
Слайд 7Взаимное расположение сферы и плоскости (продолжение)
Если расстояние от центра сферы до плоскости
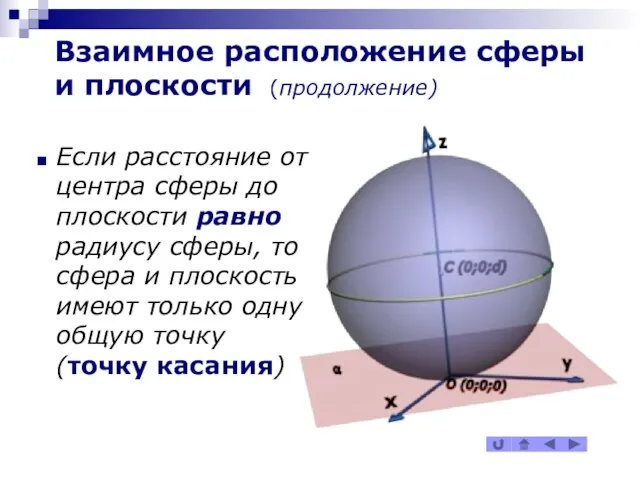
равно радиусу сферы, то сфера и плоскость имеют только одну общую точку (точку касания)
Слайд 8Взаимное расположение сферы и плоскости (окончание)
Если расстояние от центра сферы до плоскости
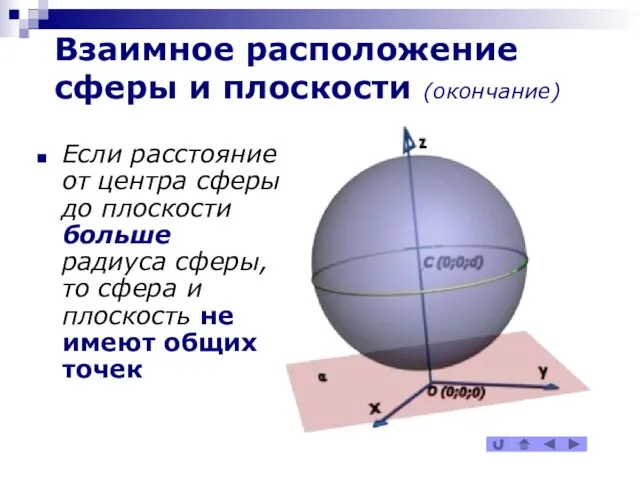
больше радиуса сферы, то сфера и плоскость не имеют общих точек
Слайд 9Касательная плоскость к сфере
Плоскость, имеющая только одну общую точку со сферой называется
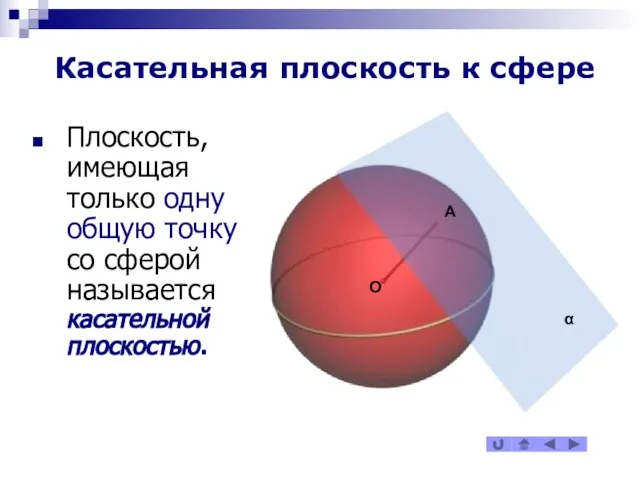
касательной плоскостью.
Слайд 10Касательная плоскость к сфере (продолжение)
Теорема: Радиус сферы, проведенный в точку касания сферы

и плоскости, перпендикулярен к касательной плоскости.
Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Слайд 11Площадь сферы, объем шара
(продолжение)
Теорема Архимеда
Объем шара в полтора раза меньше объема описанного

вокруг него цилиндра, а площадь поверхности шара в полтора раза меньше площади полной поверхности того же цилиндра:
V= (2/3)V1 S= (2/3)S1
где
V1 – объем описанного цилиндра,
S1 – площадь полной поверхности этого цилиндра
Слайд 12Площадь сферы, объем шара
Площадь поверхности шара радиуса R равна учетверенной площади большого

круга:
S=4πR²
Объем шара радиуса R равен V = (4/3)πR³











 ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Простейшие задачи в координатах
Простейшие задачи в координатах Логические законы и правила
Логические законы и правила Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Признаки равенства треугольников 7 класс
Признаки равенства треугольников 7 класс Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Площади многоугольников
Площади многоугольников Сумма углов в треугольнике
Сумма углов в треугольнике Прямоугольник
Прямоугольник Масштаб. Длина окружности и площадь круга
Масштаб. Длина окружности и площадь круга Осевая и центральная симметрии
Осевая и центральная симметрии Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:
Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:  Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Скалярное произведение векторов
Скалярное произведение векторов Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Прямоугольный параллелепипед (2 класс)
Прямоугольный параллелепипед (2 класс) Геометрия 10 класс - презентация по Геометрии
Геометрия 10 класс - презентация по Геометрии Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________
Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________ Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Установление соотношения между сторонами и углами прямоугольного треугольника
Установление соотношения между сторонами и углами прямоугольного треугольника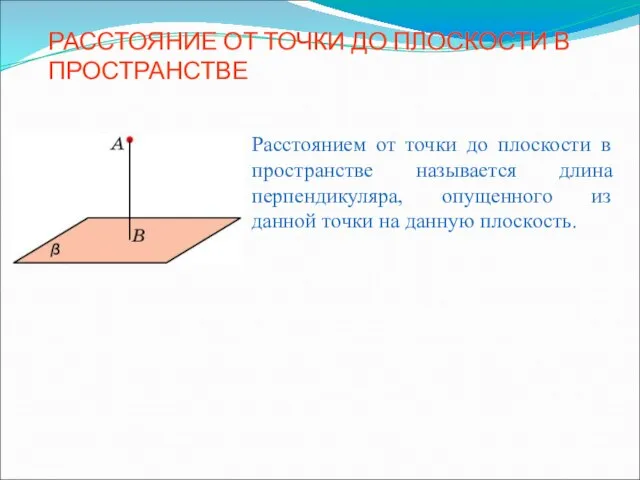 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Окружность и круг
Окружность и круг Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Свойства пирамиды с равными боковыми ребрами
Свойства пирамиды с равными боковыми ребрами Описанная окружность
Описанная окружность