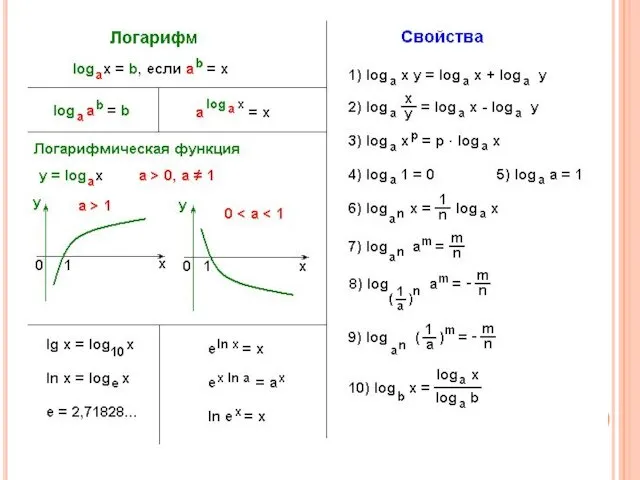
Слайд 2ОПРЕДЕЛЕНИЕ
Логарифм числа a по основанию b определяется как показатель степени, в которую

надо возвести число b, чтобы получить число a. Обозначение: logba. Из определения следует, что записи logba = x и bx = a эквивалентны.
Где b не = 1, a>0, b > 0
Пример: log28 = 3, потому что 23 = 8.
Слайд 3ВЕЩЕСТВЕННЫЙ ЛОГАРИФМ
Логарифм вещественного числа logba имеет смысл при .
Наиболее широкое применение нашли

следующие виды логарифмов:
Десятичные: основание: число 10.
Натуральные: основание: e (число Эйлера).
Двоичные: основание: число 2. Они применяются в теории информации и информатике.
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например: . Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема
Слайд 5НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
Для производной натурального логарифма справедлива простая формула
По этой причине в математических

исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.
Слайд 6ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов) до

изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
ФизикаФизика — интенсивность звука (децибелы).
АстрономияАстрономия — шкала яркости звёзд.
ХимияХимия — активность водородныхХимия — активность водородных ионовХимия — активность водородных ионов (pH).
СейсмологияСейсмология — шкала Рихтера.
Теория музыки — нотная шкала.
Слайд 7СВОЙСТВА ЛОГАРИФМОВ
1) log b = 1 , так как b 1 =

b .
b
2) log 1 = 0 , так как b 0 = 1 .
b
3) log a = a
b b
основное тригонометрическое тождество
Слайд 9СВОЙСТВА ЛОГАРИФМОВ
4) Логарифм произведения равен сумме логарифмов сомножителей:
log ( ab ) =

log a + log b .
5) Логарифм частного равен разности логарифмов делимого и делителя:
log ( a / b ) = log a – log b .
Слайд 10СВОЙСТВА ЛОГАРИФМОВ
6) Логарифм степени равен произведению показателя степени на логарифм её основания:
Log

( b k ) = k · log b .
7) Логарифм основания в степени равен произведению степени в минус первой степени на логарифм её основания
Log n b= 1/n log b
a a









 Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А.
Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А. Циклоида
Циклоида Площади фигур. Зачёт
Площади фигур. Зачёт Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Решение прямоугольных треугольников
Решение прямоугольных треугольников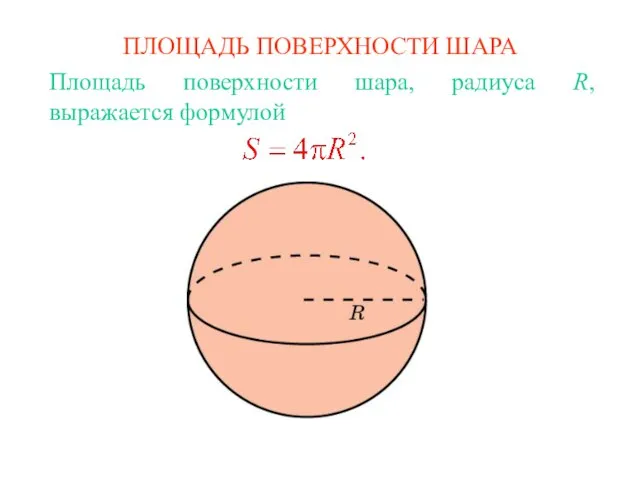 Площадь поверхности шара
Площадь поверхности шара Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Скрещивающиеся прямые
Скрещивающиеся прямые Флексагоны флексоры
Флексагоны флексоры Сфера. Шар
Сфера. Шар Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ От сферы к плоскости
От сферы к плоскости Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Правильные многогранники
Правильные многогранники Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Чудеса симметрии
Чудеса симметрии Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Геометрия в жизни
Геометрия в жизни Египетский треугольник
Египетский треугольник Задачи на построение сечений
Задачи на построение сечений История возникновения Геометрии
История возникновения Геометрии История геометрии
История геометрии Задачи на готовых чертежах
Задачи на готовых чертежах Сечения
Сечения Площади плоских геометрических фигур
Площади плоских геометрических фигур