Содержание
- 2. Содержание Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы
- 3. Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад. Индийские
- 4. Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476). Основным математическим трудом
- 5. Арабские ученые аль-Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через
- 6. В Европе основы геометрии закладывал древнегреческий астроном и математик Аристарх Самосский (310-230 лет до Р.Х.) в
- 7. Греческий математик Клавдий Птолемей (87-165 от Р.Х) также внес большой вклад в развитие тригонометрии. Он расширил
- 8. sin²α+cos²α =1 tgα= sinα/cos α ctgα = cosα/sin α tgα ctgα =1 tg²α+1=1/cos²α ctg²α+1=1/sin²α Основные тригонометрические
- 9. Формулы сложения cos(α-β) = cosα cosβ+sinα sinβ cos(α+β) = coα cosβ-sinα sinβ sin(α-β) = sinα cosβ-cosα
- 10. Фомулы суммы и разности синусов, косинусов sin α+ sin β =2 sin(α+β)/2 cos(α-β) /2 sin α-
- 11. Формулы двойного аргумента sin2α=2sinα cosα cos2α= cos²α - sin²α cos2α=1-2sin²α cos2α= 2cos²α-1 tg2α= 2tgα/1- tg²α
- 12. Формулы половинного аргумента sin²α/2=1- cosα/2 cos²α/2=1+cosα/2 tg²α/2=1- cosα/1+cosα tgα/2= sinα/1+cosα tgα/2= 1-cosα / sinα
- 13. Тригонометрические формулы применяются практически во всех областях геометрии, физики, инженерного дела. Большое значение имеет техника триангуляции,
- 14. оптика медицина, фармацевтика химия
- 15. сейсмология метеорология картография
- 16. системы навигации спутников астрономия архитектура
- 18. Скачать презентацию














 Решение треугольников. Измерительные работы на местности. Тема урока:
Решение треугольников. Измерительные работы на местности. Тема урока: Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ Преобразования на плоскости
Преобразования на плоскости Геометрия 8класс Учитель Бужан Л.В.
Геометрия 8класс Учитель Бужан Л.В. Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций От сферы к плоскости
От сферы к плоскости Применение параллелограмма
Применение параллелограмма Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья
Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья Фракталы и их применение в наши дни.
Фракталы и их применение в наши дни. Магические квадраты (6 класс)
Магические квадраты (6 класс) Центральная симметрия Занятие 28
Центральная симметрия Занятие 28 Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Правильный додекаэдр
Правильный додекаэдр Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Понятие объема. Объем призмы
Понятие объема. Объем призмы Почему квадрат?
Почему квадрат? Геометрия 10 класс - презентация по Геометрии
Геометрия 10 класс - презентация по Геометрии Бозон Хиддинса
Бозон Хиддинса Построение геометрических тел
Построение геометрических тел ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Презентация на тему: Сечение
Презентация на тему: Сечение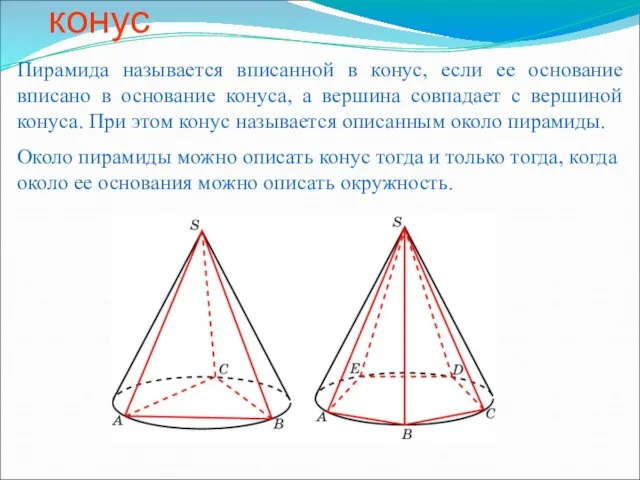 Пирамида, вписанная в конус
Пирамида, вписанная в конус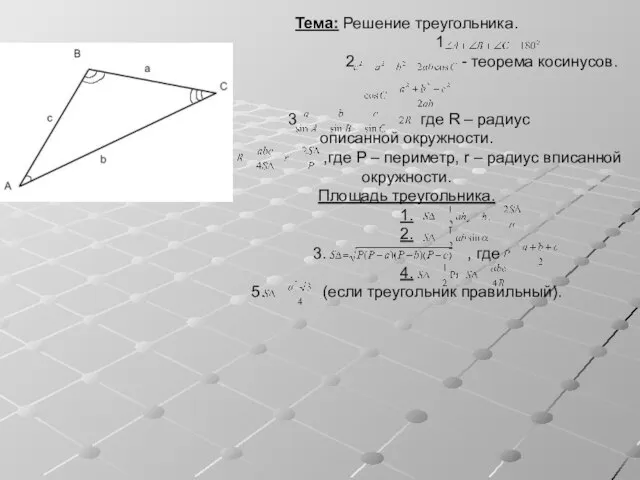 Решение треугольника
Решение треугольника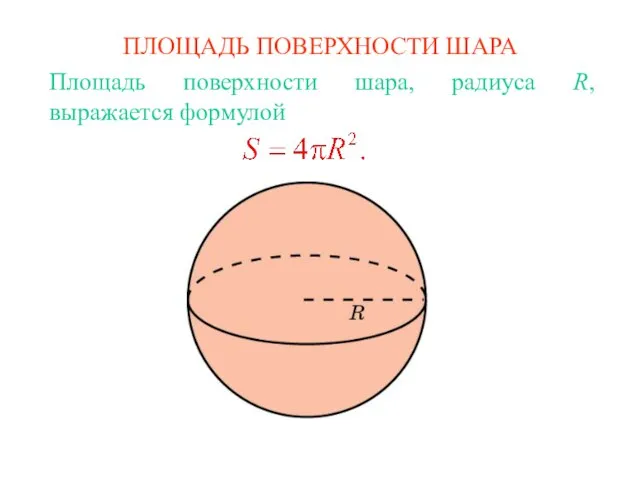 Площадь поверхности шара
Площадь поверхности шара Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Решение треугольников. Измерительные работы на местности
Решение треугольников. Измерительные работы на местности Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур