Слайд 2Работу выполнили
Ученицы 11 класса
МОУ «Тугустемирская СОШ»
Кудряшова Наташа
Дусаева Гульнара

Слайд 3Теорема
Объем конуса равен одной трети произведения площади основания на высоту.

Слайд 4Доказательство
Рассмотрим конус с объемом V, радиусом R, высотой h и вершиной в

точке О. Введем ось Оx так, как показано на рисунке 1 (ОМ – ось конуса). Произвольное сечение конуса плоскостью, перпендикулярной к оси Оx, является кругом с центром в точке М1 пересечения этой плоскости с осью Оx. Обозначим радиус этого круга через R1, а площадь сечения через S(x), где x – абсцисса точки М1. из подобия прямоугольных треугольников ОМ1А1 и ОМА следует, что
Откуда . Так как ,то
Применяя основную формулу для вычисления объемов тел при а = 0,b = n, получаем
Площадь S основания конуса равна πR2, S = πR2 , поэтому
Теорема доказана.
Слайд 5Следствие
Объем V усеченного конуса, высота которого равна h ,а площади оснований

равны S и S1, вычисляется по формуле:




 Смежные и вертикальные углы
Смежные и вертикальные углы Теорема Пифагора задачи
Теорема Пифагора задачи Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Определение и признак перпендикулярности плоскостей
Определение и признак перпендикулярности плоскостей Прямоугольный параллелепипед
Прямоугольный параллелепипед Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса 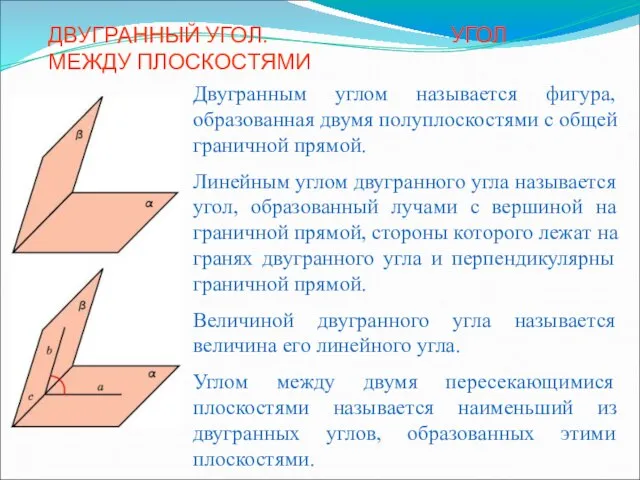 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Развёртка куба
Развёртка куба Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Применение параллелограмма
Применение параллелограмма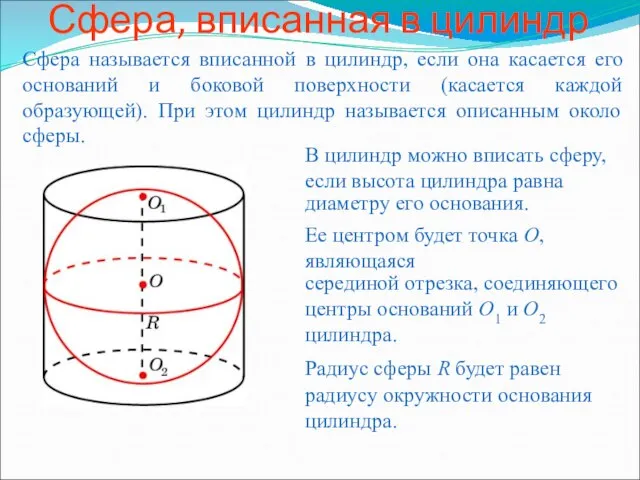 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Музей истории четырёхугольников
Музей истории четырёхугольников Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Пирамиды
Пирамиды Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Путешествие в страну Геометрия
Путешествие в страну Геометрия Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Объём пирамиды
Объём пирамиды Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Луч и угол (7 класс)
Луч и угол (7 класс)