Задачи на построение сечений

Сечение Может быть построено по трем точкам, не лежащим на одной прямой, а также если заданы точка и прямая, причем точка не лежит на прямой.
Рассмотрим задачи на построение сечений в порядке возрастания их сложности.
Задачи на построение сечений

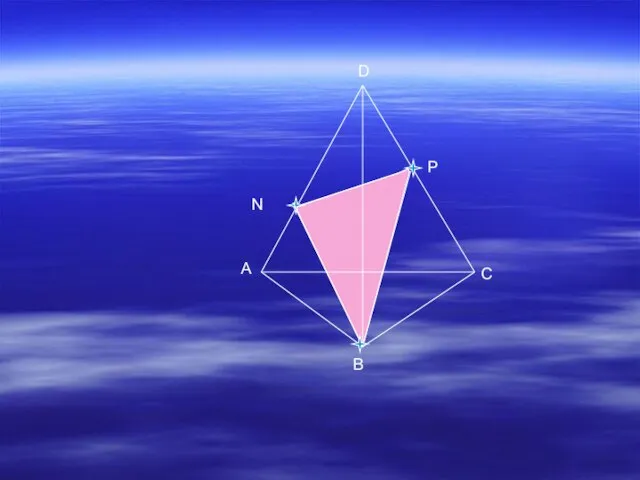
Э
Дано:ABCD- тетраэдр, N ADC, P ADC. Построить сечение данного тетраэдра через точки N, P, B.
Э
Э
Задача №1.

B
A
C
D
N
P

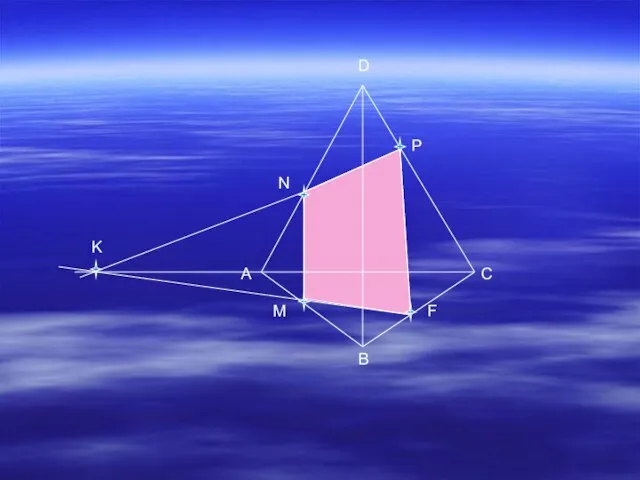
Э
Дано:ABCD-тетраэдр, N AD, P CD, F BC. Построить сечение проходящее через данные точки.
Э
Э
Э
Задача №2.

A
B
C
D
M
N
P
K
F

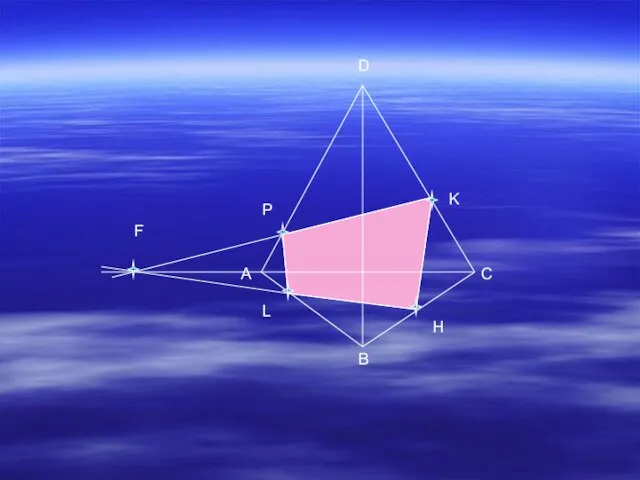
Дано:ABCD-тетраэдр, K DC, M ABC, N ACD. Построить сечение MNK.
Э
Э
Э
Задача №3

A
B
C
D
K
P
L
H
F

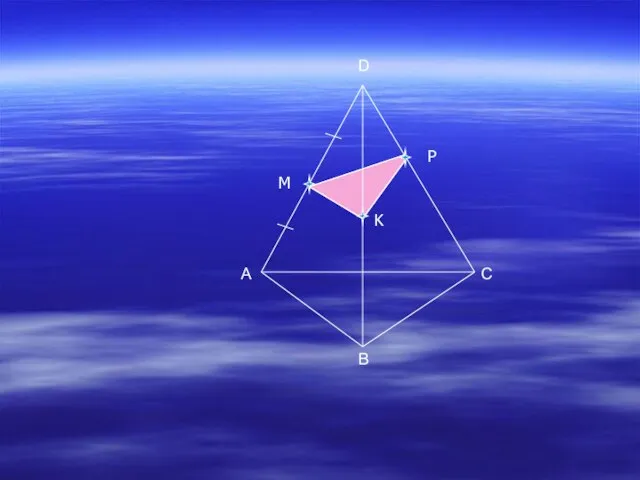
Э
Дано:ABCD-тетраэдр, M AD, AM=MD, P DC, DP/PC=1/3. Построить сечение плоскостью, проходящей через точки M и P и параллельно BC.
Задача №4.
Э
Э

A
B
C
D
M
P
K