Бриллианты элементарной геометрии - презентация по Геометрии_

Вопросы для повторения
Теорема косинусов
Подобие треугольников
Вписанный угол
Свойство вписанных углов опирающихся на одну и туже дугу.
Вписанный многоугольник
Формулы приведения

Новые термины
ЧЕВИАНА - отрезок соединяющий вершину треугольника с произвольной точкой противоположной стороны.
ТРИСЕКТРИСА - прямые проходящие через вершину угла и делящие его на три равные части.

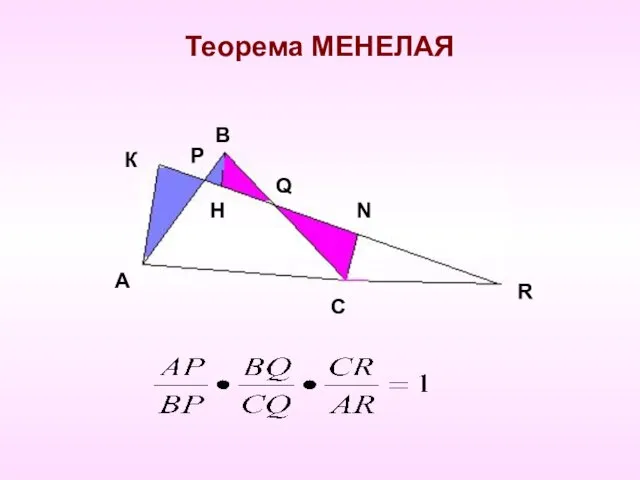
Теорема МЕНЕЛАЯ
К
Р
А
R
Н
Q
N
В
С

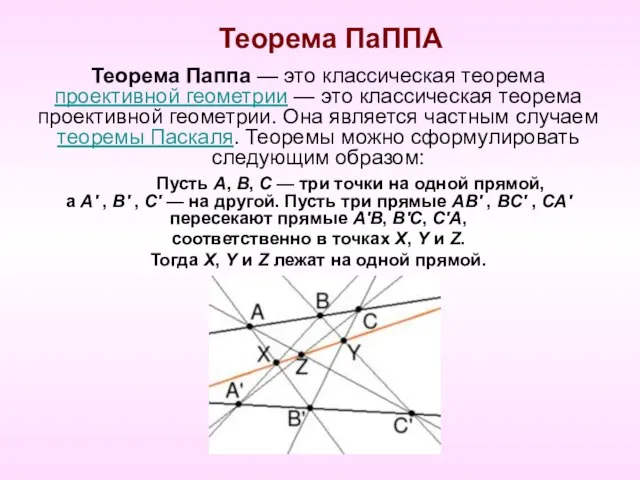
Теорема ПаППА
Теорема Паппа — это классическая теорема проективной геометрии — это классическая теорема проективной геометрии. Она является частным случаем теоремы Паскаля. Теоремы можно сформулировать следующим образом:
Пусть A, B, C — три точки на одной прямой, а A' , B' , C' — на другой. Пусть три прямые АВ' , BC' , CA' пересекают прямые A'B, B'C, C'A,
соответственно в точках X, Y и Z.
Тогда X, Y и Z лежат на одной прямой.

Теоремы Брахмагупта
Дан произвольный 4-х угольник около которого можно описать окружность.
Пусть длины его сторон a, b, c, d. Тогда площадь
Его будет вычисляться по формуле
S=√(p-a) (p-b) (p-c) (p-d)
Если четырехугольник таков, что в него можно и вписать и описaть около
Него окружность, то его площадь может быть вычислена по формуле
S=√a b c d

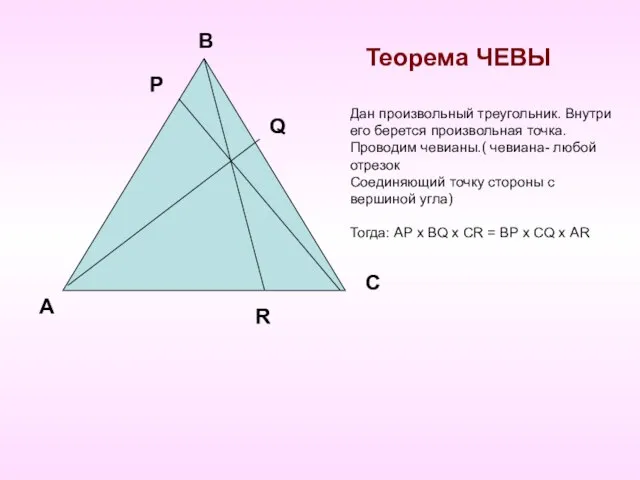
Теорема ЧЕВЫ
А
В
С
Р
Q
R
Дан произвольный треугольник. Внутри его берется произвольная точка.
Проводим чевианы.( чевиана- любой отрезок
Соединяющий точку стороны с вершиной угла)
Тогда: AP х ВQ х CR = BP х CQ х AR

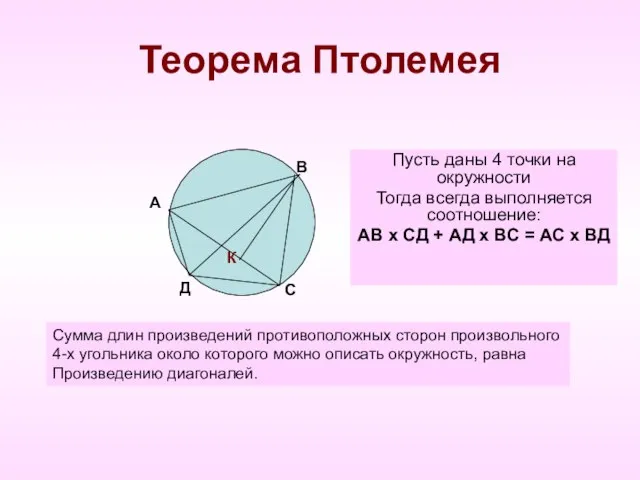
Теорема Птолемея
Пусть даны 4 точки на окружности
Тогда всегда выполняется соотношение:
АВ х СД + АД х ВС = АС х ВД
Сумма длин произведений противоположных сторон произвольного
4-х угольника около которого можно описать окружность, равна
Произведению диагоналей.
С
Д
В
А
К

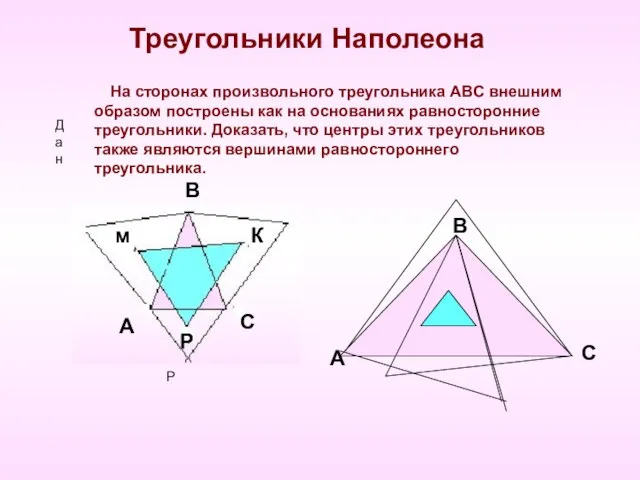
Треугольники Наполеона
Дан
На сторонах произвольного треугольника АВС внешним образом построены как на основаниях равносторонние треугольники. Доказать, что центры этих треугольников также являются вершинами равностороннего треугольника.
.
Р
А
В
С
Р
А
В
м
С
К

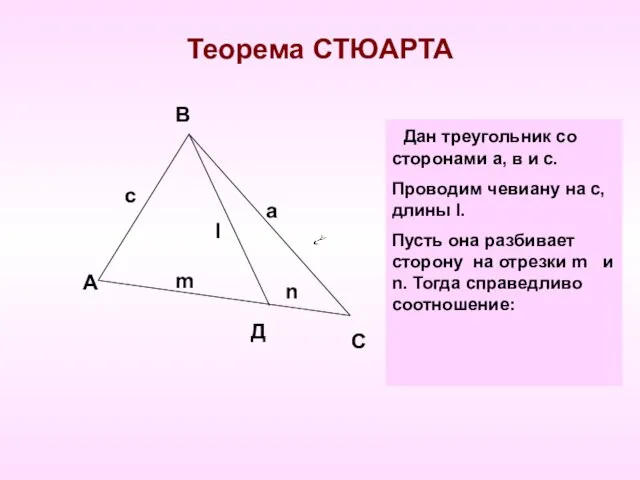
Теорема СТЮАРТА
А
В
n
с
l
а
m
С
Д
Дан треугольник со сторонами а, в и с.
Проводим чевиану на с, длины l.
Пусть она разбивает сторону на отрезки m и n. Тогда справедливо соотношение:

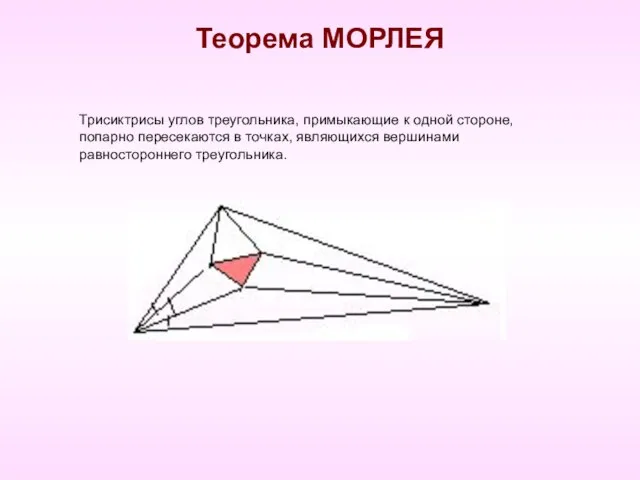
Теорема МОРЛЕЯ
Трисиктрисы углов треугольника, примыкающие к одной стороне, попарно пересекаются в точках, являющихся вершинами равностороннего треугольника.

Задача
Рассадите 10 деревьев в десяти рядах, так чтобы в каждом ряду было
По 3 дерева.

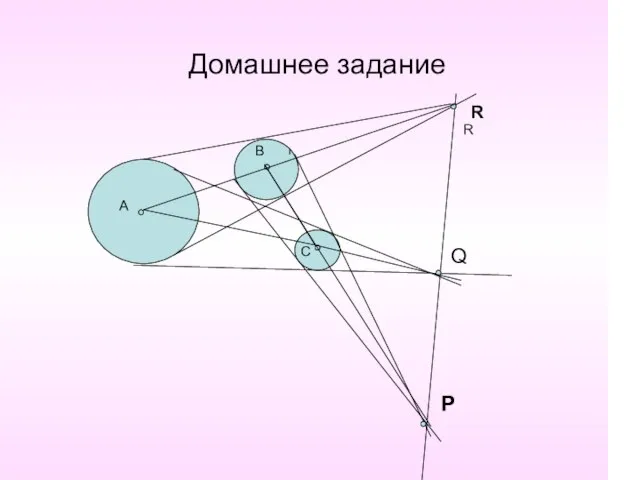
Домашнее задание
R
R
Q
P
А
В
С