Окружности

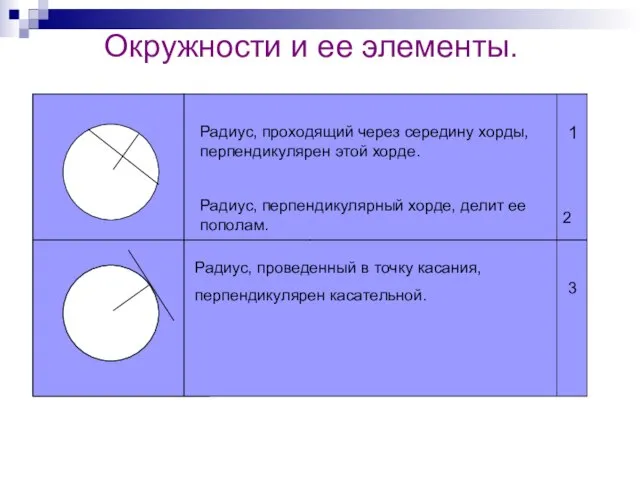
Окружности и ее элементы.
.
Радиус, проходящий через середину хорды, перпендикулярен этой хорде.
Радиус, перпендикулярный хорде, делит ее пополам.
Радиус, проведенный в точку касания,
перпендикулярен касательной.
1
3
2

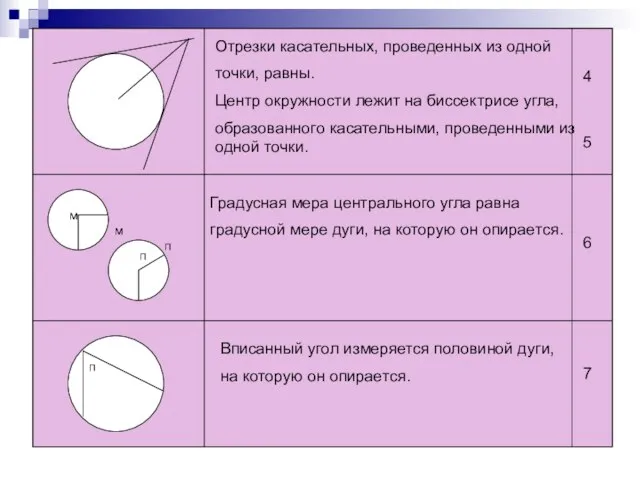
Отрезки касательных, проведенных из одной
точки, равны.
Центр окружности лежит на биссектрисе угла,
образованного касательными, проведенными из одной точки.
Градусная мера центрального угла равна
градусной мере дуги, на которую он опирается.
Вписанный угол измеряется половиной дуги,
на которую он опирается.
п
п
п
м
м
4
5
6
7

Вписанные углы, опирающиеся на одну дугу,
равны.
Вписанные угол, опирающийся на диаметр,
равен 90градусав.
Если две хорды окружности пересекаются, то
произведение отрезков одной хорды равно
произведению отрезков другой хорды:
AxD=MxH
М
D
H
A
8
9
10

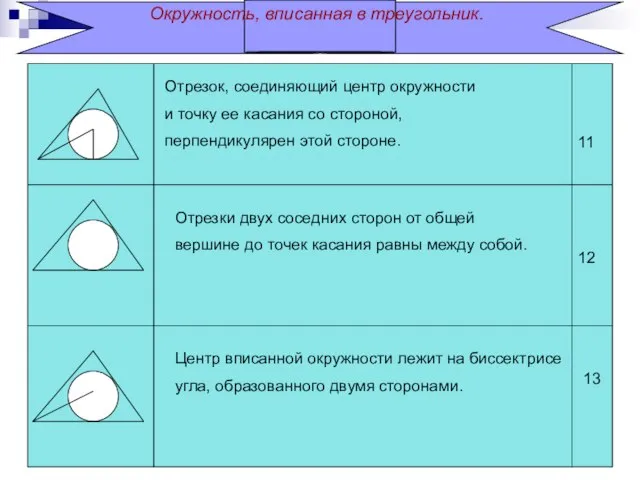
Окружность, вписанная в треугольник.
Отрезок, соединяющий центр окружности
и точку ее касания со стороной,
перпендикулярен этой стороне.
Отрезки двух соседних сторон от общей
вершине до точек касания равны между собой.
Центр вписанной окружности лежит на биссектрисе
угла, образованного двумя сторонами.
11
12
13

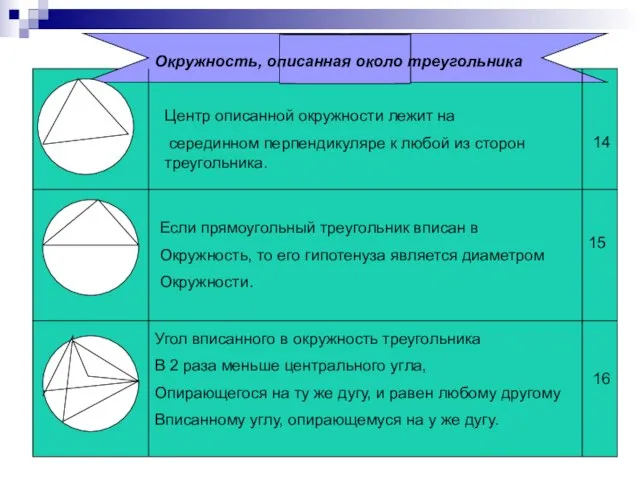
Окружность, описанная около треугольника
Центр описанной окружности лежит на
серединном перпендикуляре к любой из сторон треугольника.
Если прямоугольный треугольник вписан в
Окружность, то его гипотенуза является диаметром
Окружности.
Угол вписанного в окружность треугольника
В 2 раза меньше центрального угла,
Опирающегося на ту же дугу, и равен любому другому
Вписанному углу, опирающемуся на у же дугу.
14
15
16

пример
1
Из точки А к окружности с центром О проведены касательные АВ с АС<В и С-точки
касания>. Отрезки АО и ВС пересекаются в точке К. Найдите радиус окружности, если ВС=6, АК=2,25.
О
В
С
А
решение
Т.к АБС- равнобедренный, а АК- его биссектриса(4),(5),то АК ВС и ВК=СК=3
Проведем радиус ОВ, тогда
АОВ- прямоугольный, ВК- его высота. Тогда ВКxВК=ОКxАК, откуда ОК=9:2,25=9:(9:4)=4.
Ответ:4