Содержание
- 2. Элементы треугольника Виды треугольников Признаки равенства треугольников - Первый признак - Второй признак - Третий признак
- 4. Равнобедренный Равносторонний Разносторонний виды треугольников
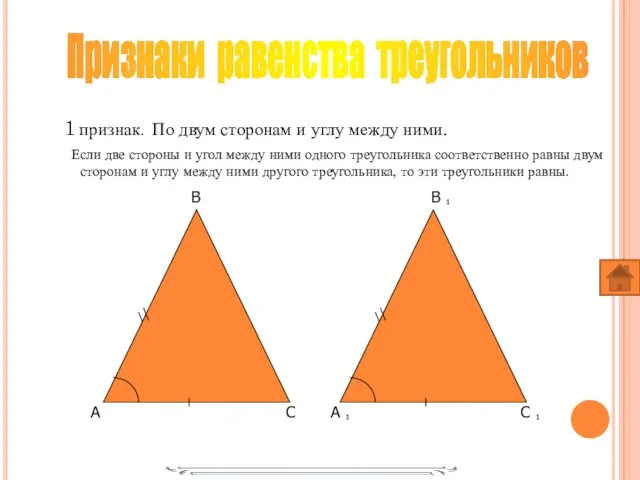
- 5. 1 признак. По двум сторонам и углу между ними. Если две стороны и угол между ними
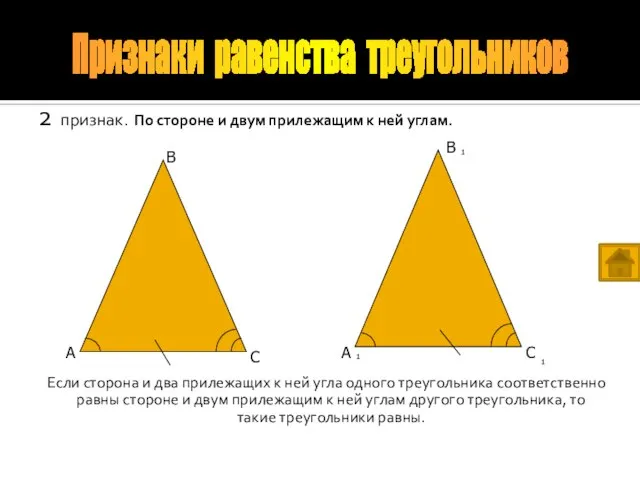
- 6. 2 признак. По стороне и двум прилежащим к ней углам. Если сторона и два прилежащих к
- 7. 3 признак. По трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника,
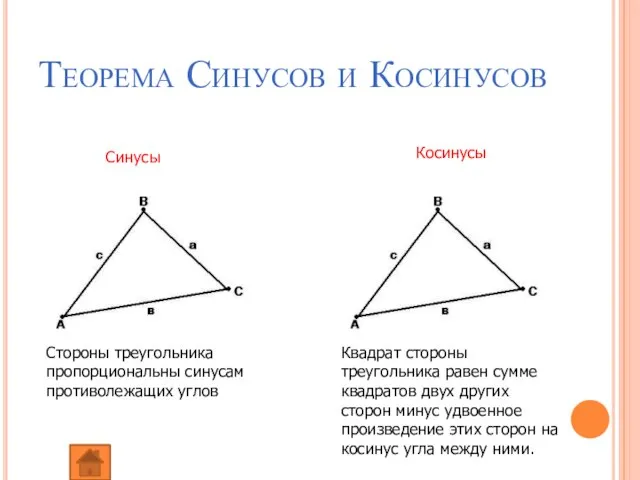
- 8. Теорема Синусов и Косинусов Стороны треугольника пропорциональны синусам противолежащих углов Квадрат стороны треугольника равен сумме квадратов
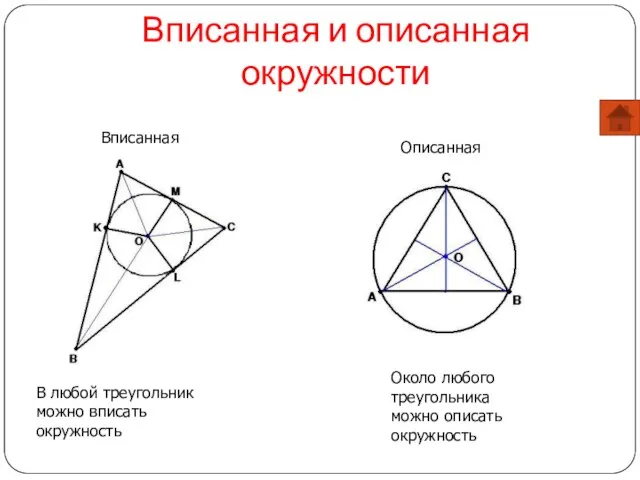
- 9. Вписанная и описанная окружности Вписанная Описанная В любой треугольник можно вписать окружность Около любого треугольника можно
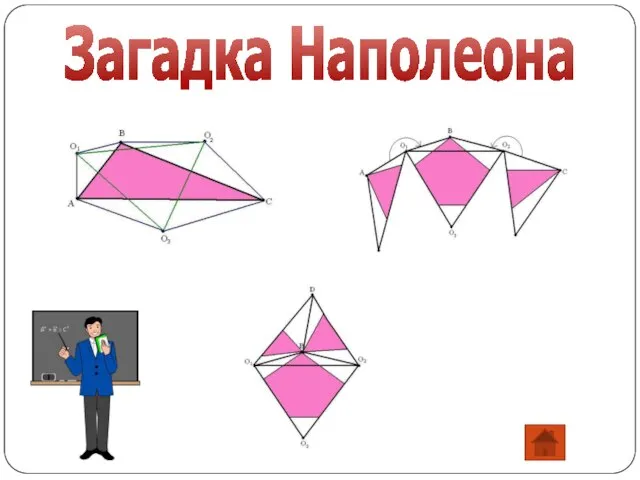
- 10. Наполеон Бонапарт Французский император Наполеон Бонапарт был любителем математики. Одно из свидетельств этому – несколько составленных
- 11. Загадка Наполеона
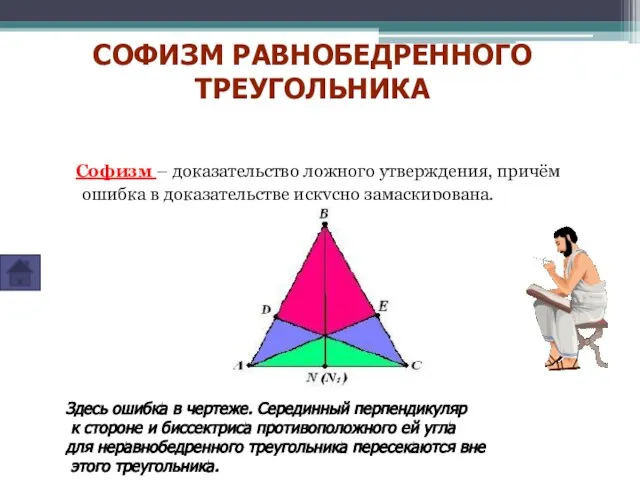
- 12. Софизм – доказательство ложного утверждения, причём ошибка в доказательстве искусно замаскирована. Здесь ошибка в чертеже. Серединный
- 14. Скачать презентацию




 Четырехугольники 9 класс
Четырехугольники 9 класс Цилиндр и конус - презентация по Геометрии
Цилиндр и конус - презентация по Геометрии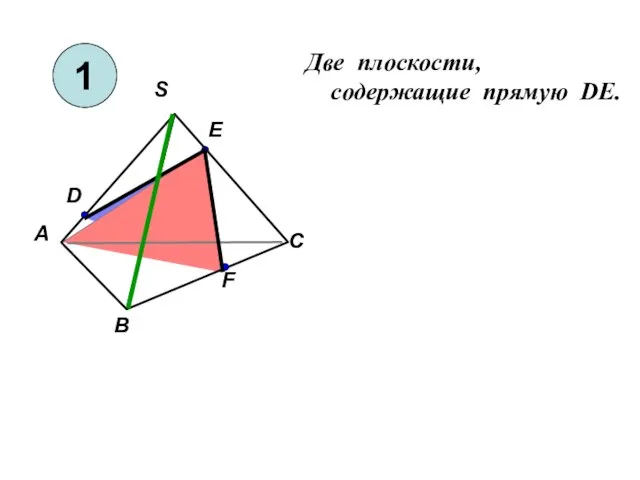 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_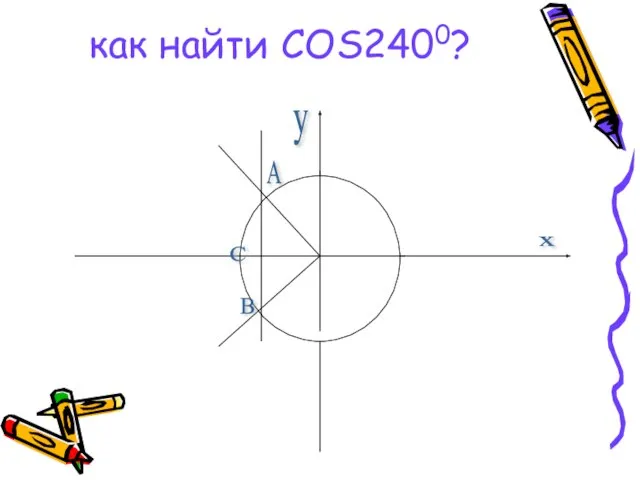 Косинус
Косинус Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций Перпендикулярные прямые на плоскости
Перпендикулярные прямые на плоскости Вписанные углы
Вписанные углы Бриллианты элементарной геометрии - презентация по Геометрии_
Бриллианты элементарной геометрии - презентация по Геометрии_ Урок повторения в 6 классе
Урок повторения в 6 классе Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми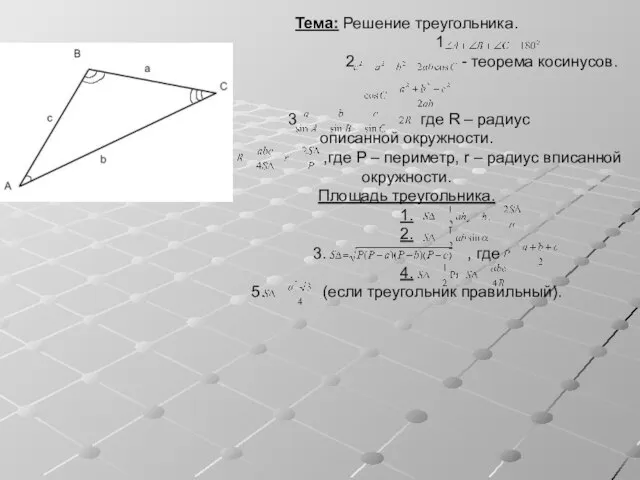 Решение треугольника
Решение треугольника Окружность в аксонометрии
Окружность в аксонометрии Что мы знаем о параллельности? - презентация по Геометрии_
Что мы знаем о параллельности? - презентация по Геометрии_ Объём пирамиды
Объём пирамиды Признаки параллельности прямых. Свойства параллельных прямых
Признаки параллельности прямых. Свойства параллельных прямых Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Параллелепипед
Параллелепипед Смежные и вертикальные углы
Смежные и вертикальные углы Теорема синусов 9 класс
Теорема синусов 9 класс Вокруг храма с линейкой и циркулем
Вокруг храма с линейкой и циркулем Длина окружности. Площадь круга
Длина окружности. Площадь круга Призма 9 класс
Призма 9 класс ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды