длин катетов .
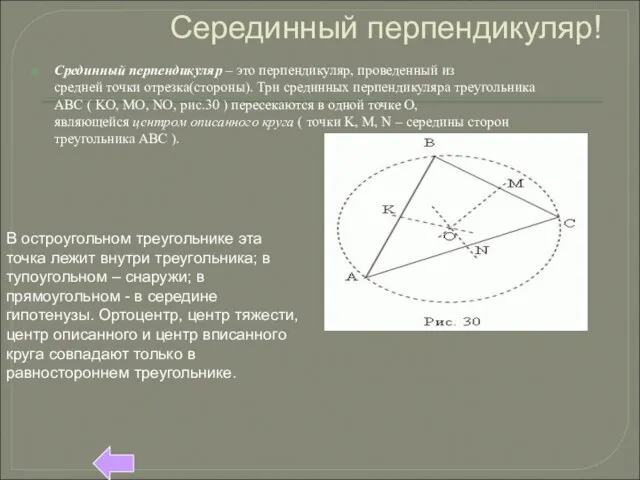
Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a, b и гипотенузой c.
Построим квадрат AKMB, используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF, сторона которого равна a+ b . Теперь ясно, что площадь квадрата CDEF равна ( a + b ) 2. С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB, то есть
c 2 + 4 ( ab / 2 ) = c 2 + 2 ab ,
отсюда,
c 2 + 2 ab = ( a + b ) 2 ,
и окончательно имеем:
c 2 = a 2 + b 2 .
В общем случае ( для произвольного треугольника ) имеем:
c 2 = a 2 + b 2 – 2ab · cos C,
где C – угол между сторонами a и b .
Соотношение сторон в произвольном треугольнике.






 Многогранники
Многогранники Четырехугольники
Четырехугольники Пентагон
Пентагон Площади фигур. Зачёт
Площади фигур. Зачёт Первый признак равенства треугольников
Первый признак равенства треугольников Теорема косинусов
Теорема косинусов Правильные многоугольники (9 класс)
Правильные многоугольники (9 класс) Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Луч и угол (7 класс)
Луч и угол (7 класс) Объём призмы
Объём призмы Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска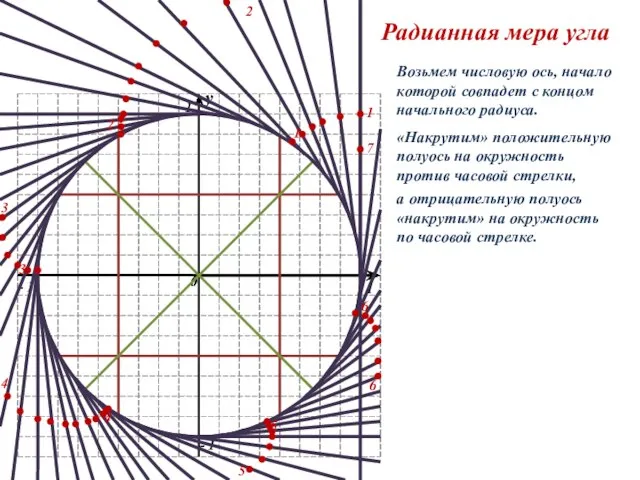 Радианная мера угла
Радианная мера угла Карточки - задания по теме "Конус"
Карточки - задания по теме "Конус" «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Почему квадрат?
Почему квадрат? Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Проецирование (8 класс)
Проецирование (8 класс) Биссектриса угла
Биссектриса угла Параллельные прямые
Параллельные прямые Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Чудеса симметрии
Чудеса симметрии Длина отрезка
Длина отрезка Скалярное произведение векторов
Скалярное произведение векторов