Содержание
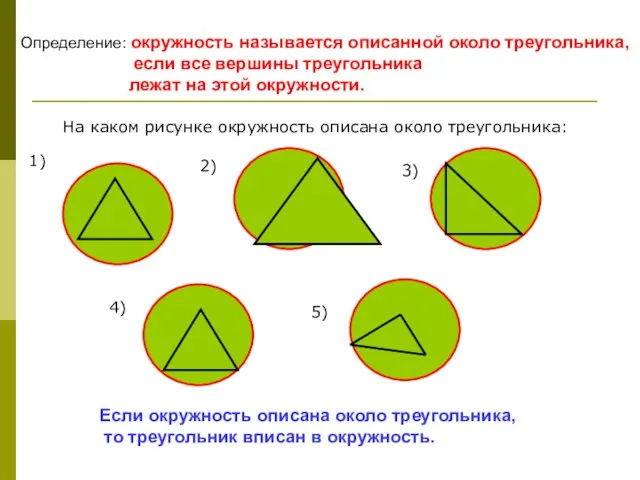
- 2. Определение: окружность называется описанной около треугольника, если все вершины треугольника лежат на этой окружности. Если окружность
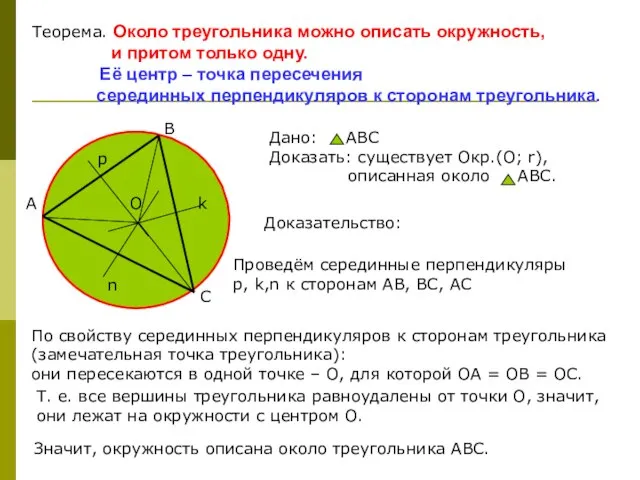
- 3. Теорема. Около треугольника можно описать окружность, и притом только одну. Её центр – точка пересечения серединных
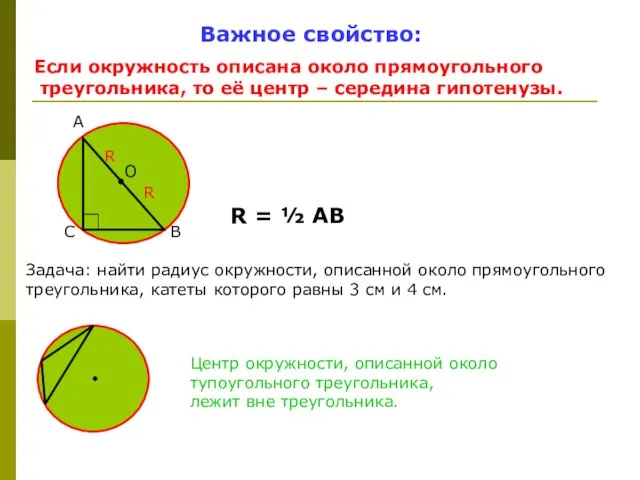
- 4. Важное свойство: Если окружность описана около прямоугольного треугольника, то её центр – середина гипотенузы. R =
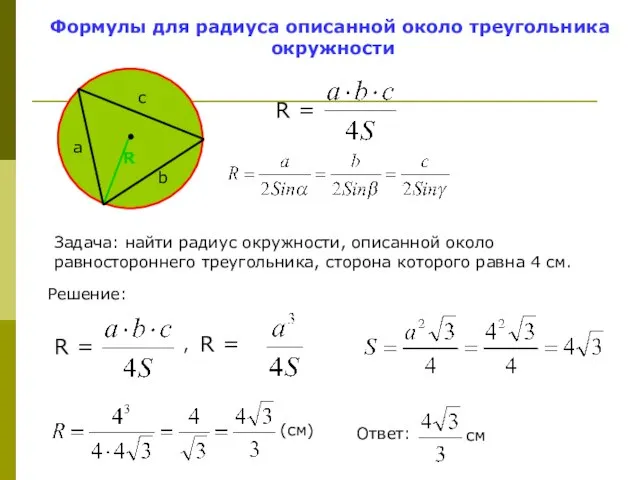
- 5. Формулы для радиуса описанной около треугольника окружности Задача: найти радиус окружности, описанной около равностороннего треугольника, сторона
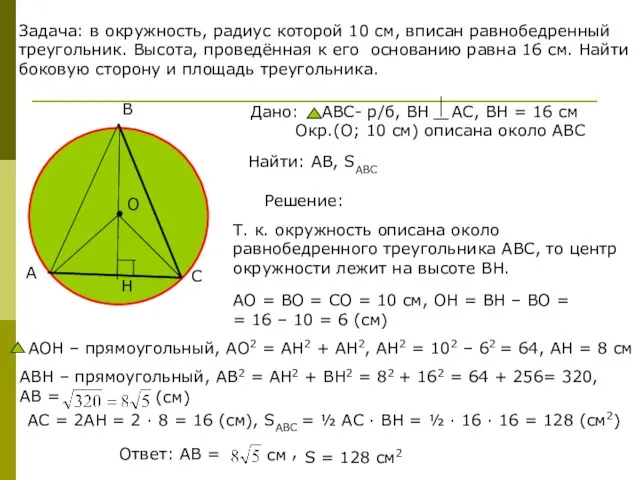
- 6. Задача: в окружность, радиус которой 10 см, вписан равнобедренный треугольник. Высота, проведённая к его основанию равна
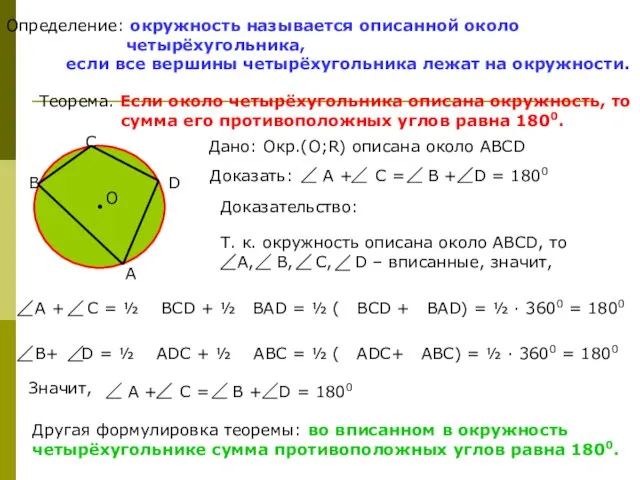
- 7. Определение: окружность называется описанной около четырёхугольника, если все вершины четырёхугольника лежат на окружности. Теорема. Если около
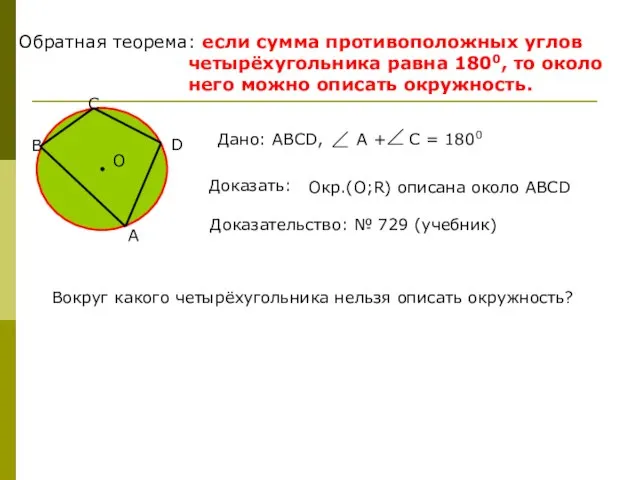
- 8. Обратная теорема: если сумма противоположных углов четырёхугольника равна 1800, то около него можно описать окружность. Доказательство:
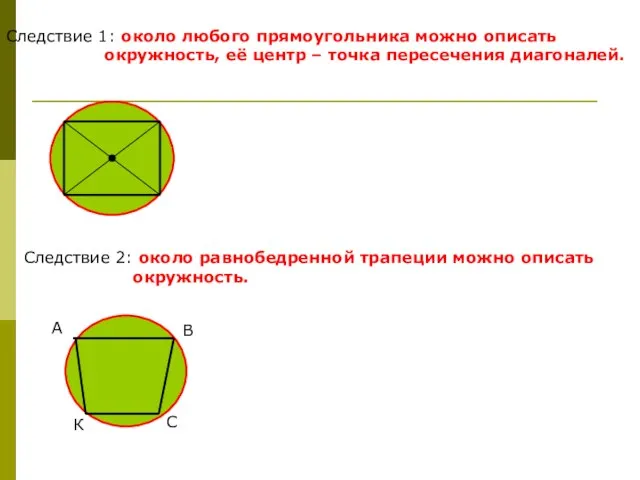
- 9. Следствие 1: около любого прямоугольника можно описать окружность, её центр – точка пересечения диагоналей. Следствие 2:
- 11. Скачать презентацию
 Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)
Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)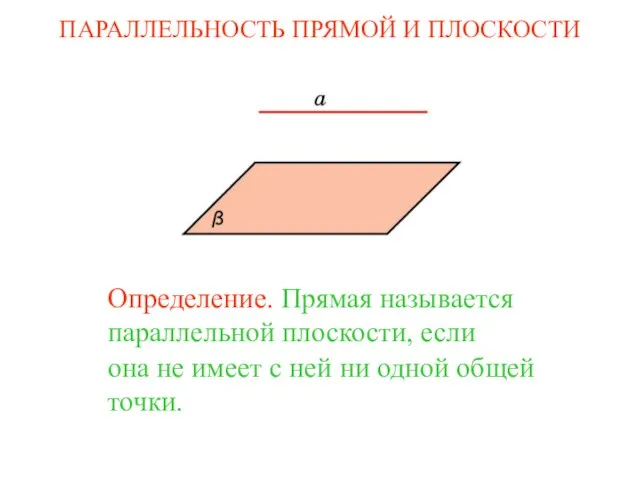 Параллельность прямой и плоскости
Параллельность прямой и плоскости Замечательные кривые
Замечательные кривые Сумма углов в треугольнике
Сумма углов в треугольнике Двугранный угол (10-11 класс) - презентация по Геометрии_
Двугранный угол (10-11 класс) - презентация по Геометрии_ Виды углов. Измерение углов
Виды углов. Измерение углов Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Свойства пирамиды с равными боковыми ребрами
Свойства пирамиды с равными боковыми ребрами Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Признаки равенства и подобия треугольников
Признаки равенства и подобия треугольников ГИА 2013 Модуль «Геометрия» № 11
ГИА 2013 Модуль «Геометрия» № 11 Теорема Пифагора задачи
Теорема Пифагора задачи Что мы знаем о параллельности? - презентация по Геометрии_
Что мы знаем о параллельности? - презентация по Геометрии_ Многогранники вокруг нас
Многогранники вокруг нас Биссектриса угла
Биссектриса угла Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах.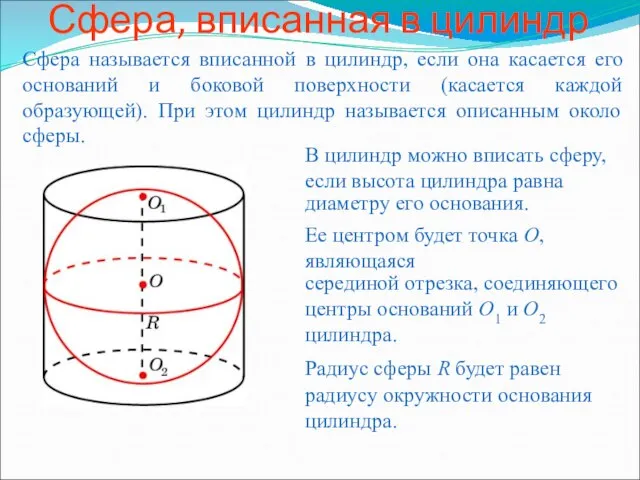 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Геометрия
Геометрия Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Площади (8 класс)
Площади (8 класс) Прямоугольник и его свойства
Прямоугольник и его свойства Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Площади плоских геометрических фигур
Площади плоских геометрических фигур Классификация геометрических объектов
Классификация геометрических объектов Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости