Содержание
- 2. Для графического решения квадратного уравнения представьте его в одном из видов: ax2 + bx +c =
- 3. Ввести функцию f(x), равную левой части и g(x) , равную правой части Построить графики функций y=f(x)
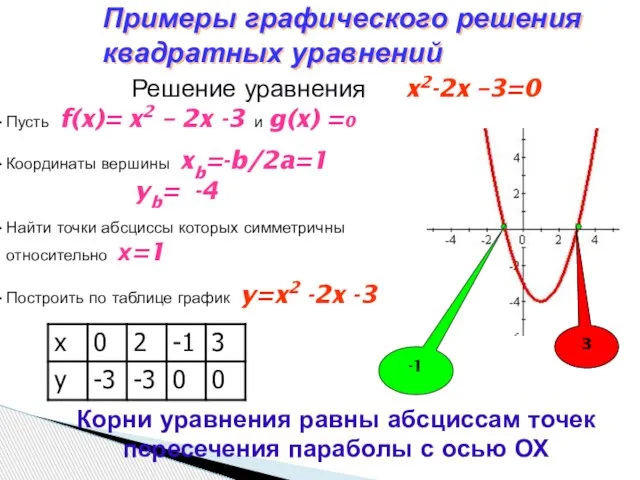
- 4. Пусть f(x)= x2 – 2x -3 и g(x) =0 Координаты вершины xb=-b/2a=1 yb= -4 Найти точки
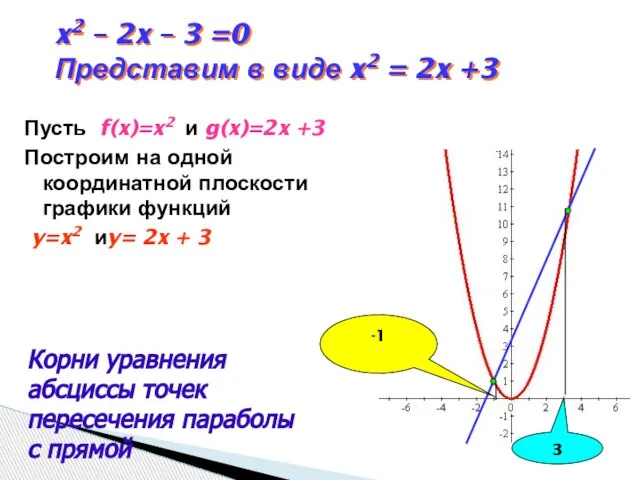
- 5. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и
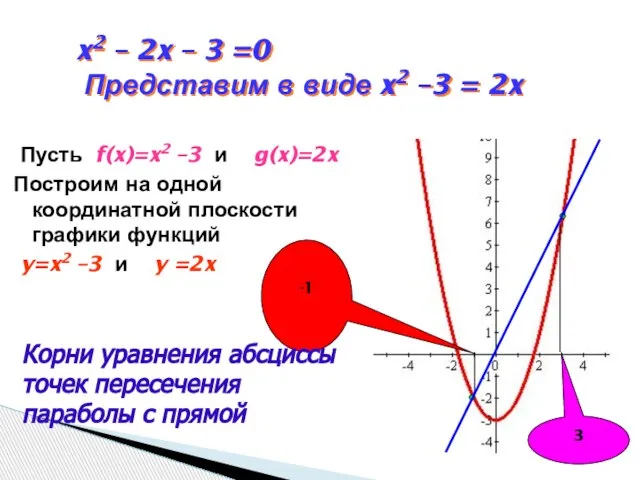
- 6. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3
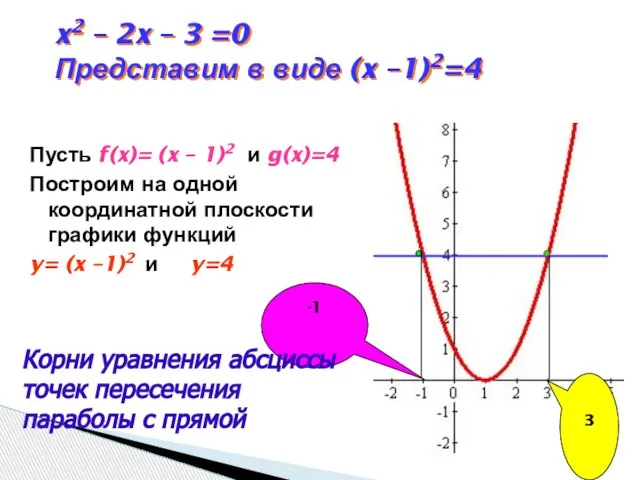
- 7. x2 – 2x – 3 =0 Представим в виде (x –1)2=4 Пусть f(x)= (x – 1)2
- 8. Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский и Евклид , Аль-Хорезми
- 10. Скачать презентацию



 Понятие многогранника
Понятие многогранника Путешествие в страну Геометрия
Путешествие в страну Геометрия Правильные многогранники
Правильные многогранники Цилиндр и конус
Цилиндр и конус Четырехугольники
Четырехугольники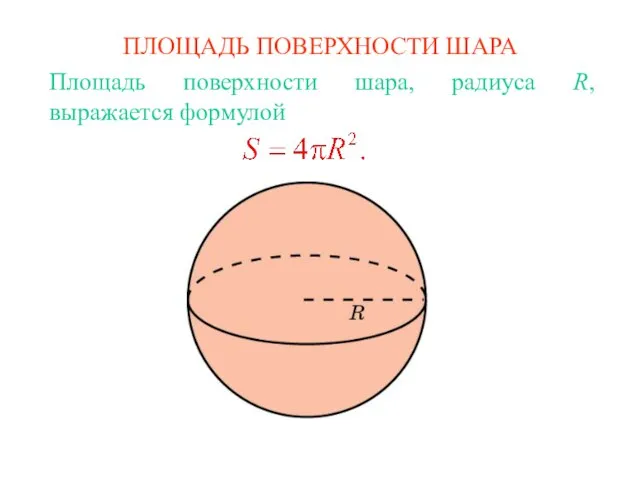 Площадь поверхности шара
Площадь поверхности шара Биссектриса угла
Биссектриса угла Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ вид разреза сечения
вид разреза сечения Плоскость
Плоскость Понятие объема. Объем призмы
Понятие объема. Объем призмы Теоремы синусов и косинусов
Теоремы синусов и косинусов Стереометрия в образах
Стереометрия в образах Тетраэдр и параллепипед
Тетраэдр и параллепипед Решение треугольников. Измерительные работы на местности
Решение треугольников. Измерительные работы на местности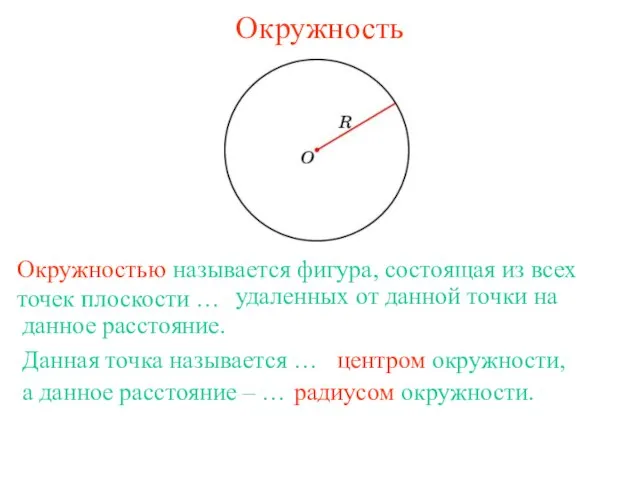 Окружность
Окружность Фракталы – геометрия природы
Фракталы – геометрия природы Многообразие многоугольников
Многообразие многоугольников Приготовьтесь к построению
Приготовьтесь к построению Окружность в аксонометрии
Окружность в аксонометрии Треугольники. Третий признак равенства
Треугольники. Третий признак равенства ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ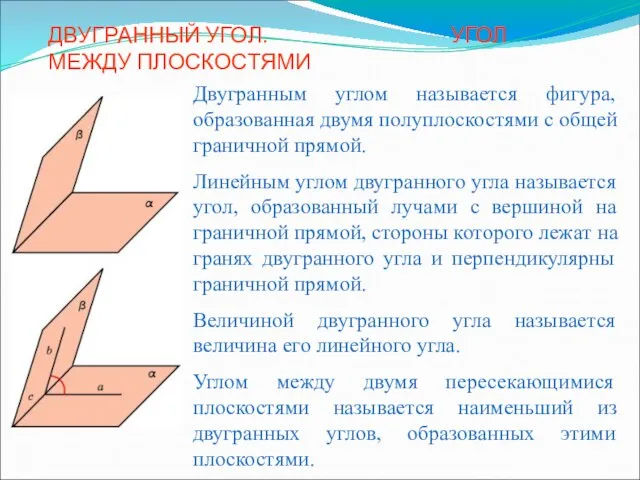 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Урок повторения в 6 классе
Урок повторения в 6 классе В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Симметрия на планете Земля
Симметрия на планете Земля