Содержание
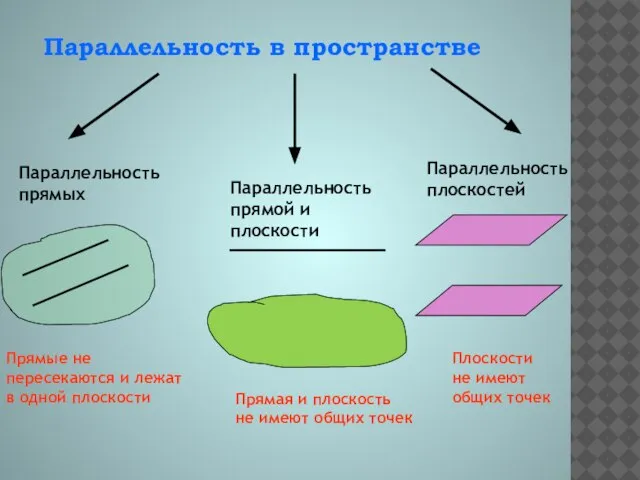
- 2. Параллельность в пространстве Параллельность прямых Параллельность прямой и плоскости Параллельность плоскостей
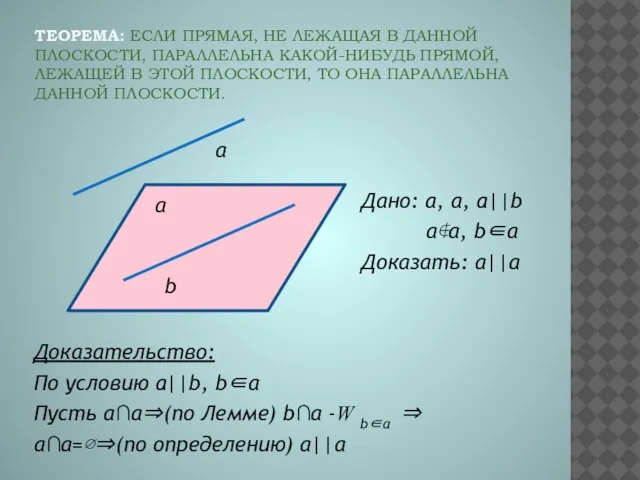
- 3. Теорема: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то
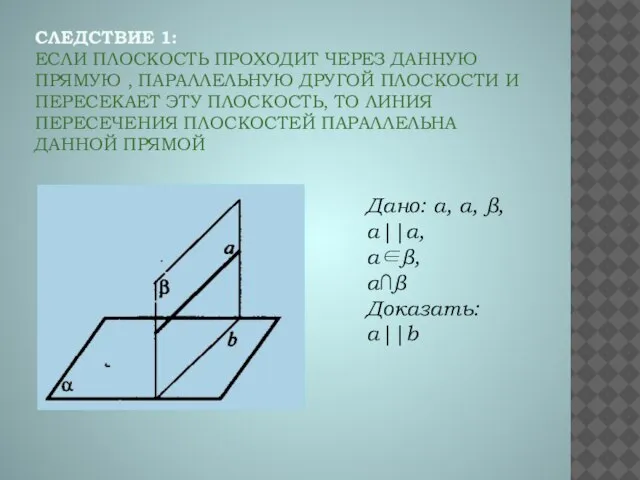
- 4. Следствие 1: Если плоскость проходит через данную прямую , параллельную другой плоскости и пересекает эту плоскость,
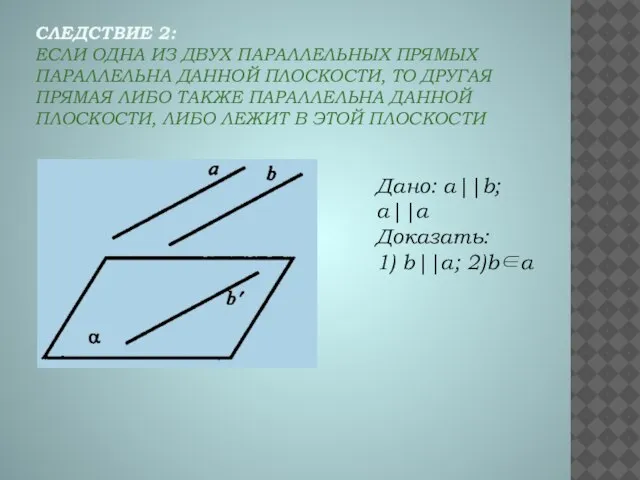
- 5. Следствие 2: Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также
- 6. Решение задач с комментариями №18 (б) №20 №22 №26
- 8. Скачать презентацию

 Площади комбинированных фигур
Площади комбинированных фигур Правильная пирамида
Правильная пирамида Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Перпендикулярные прямые на плоскости
Перпендикулярные прямые на плоскости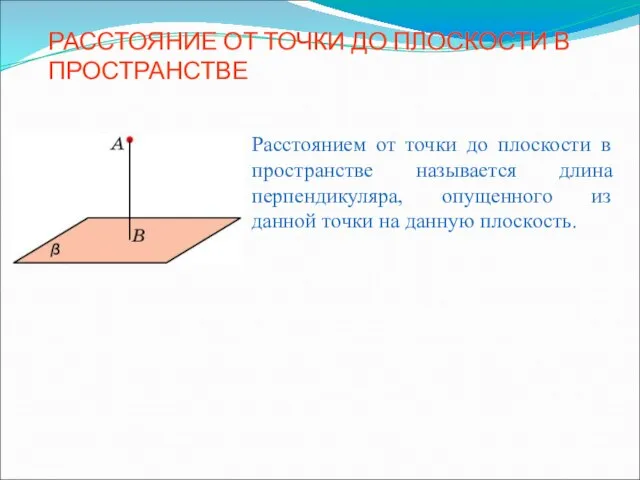 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Пентагон
Пентагон Первый признак равенства треугольников
Первый признак равенства треугольников Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Функция у = х п и ее свойства
Функция у = х п и ее свойства Правильные фигуры и тела
Правильные фигуры и тела Перемещение. Путь. Траектория 9 класс
Перемещение. Путь. Траектория 9 класс Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Цилиндр и конус - презентация по Геометрии
Цилиндр и конус - презентация по Геометрии Лист Мёбиуса
Лист Мёбиуса Окружность и круг
Окружность и круг Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Классификация геометрических объектов
Классификация геометрических объектов Площади
Площади Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс Параллелипипед
Параллелипипед Тест по теме: «Площади многоугольников»
Тест по теме: «Площади многоугольников» Координатный луч (5 класс)
Координатный луч (5 класс) Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Многогранники: виды задач и методы их решения (типовые задания С2) - 1 Графический способ решения систем укравнений
Графический способ решения систем укравнений Магические квадраты (5 класс)
Магические квадраты (5 класс)