Содержание
- 2. Определение правильного многоугольника. Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и все
- 3. Формула для вычисления угла правильного n-угольника.
- 4. Окружность, описанная около правильного многоугольника. Теорема: около любого правильного многоугольника можно описать окружность, и притом только
- 5. Окружность, вписанная в правильный многоугольник. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой
- 6. Пусть А1 А 2 …А n - правильный многоугольник, О –центр описанной окружности. При доказательстве теоремы
- 7. Докажем, что вписанная окружность только одна. Предположим, что существует другая вписанная окружность с центром О и
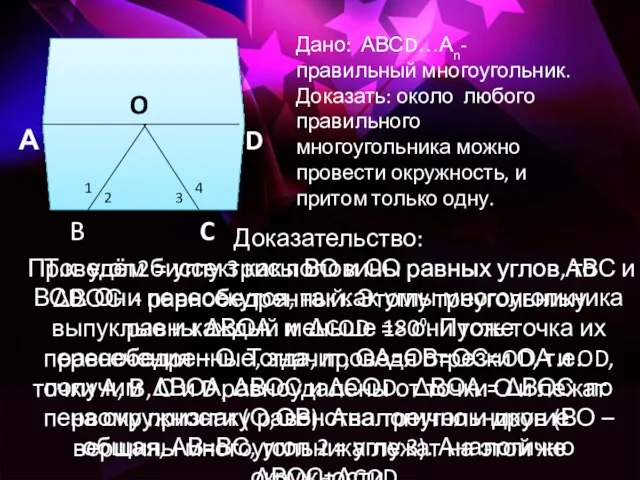
- 8. А D B C O Дано: АВСD…Аn- правильный многоугольник. Доказать: около любого правильного многоугольника можно провести
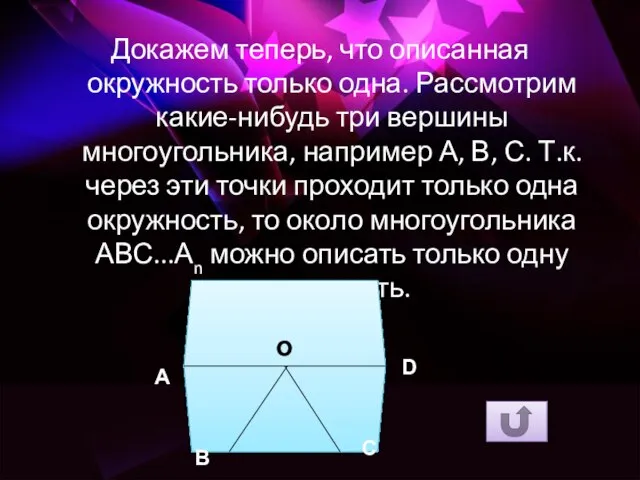
- 9. Докажем теперь, что описанная окружность только одна. Рассмотрим какие-нибудь три вершины многоугольника, например А, В, С.
- 10. Следствия. Следствие №1 Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Следствие №2
- 11. Формула для вычисления площади правильного многоугольника. Пусть S – площадь правильного n-угольника, a1 – его сторона,
- 12. Для этого, соединим центр данного многоугольника с его вершинами. Тогда многоугольник разобьется на n равных треугольников,
- 13. Формула для вычисления стороны правильного многоугольника. Выведем формулы: Для вывода этих формул воспользуемся рисунком. В прямоугольном
- 14. Полагая в формуле n = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата
- 15. Задача №1 Дано: окружность(О; R) Построить правильный n- угольник. окружность разделим на n равных дуг. Для
- 16. Задача №2 Дано: А1, А2...Аn - правильный n - угольник Построить правильный 2n-угольник Решение. Опишем около
- 17. Задача №3 Дано: отрезок PQ. Построить правильный шестиугольник , сторона которого равна данному отрезку. Решение: Построим
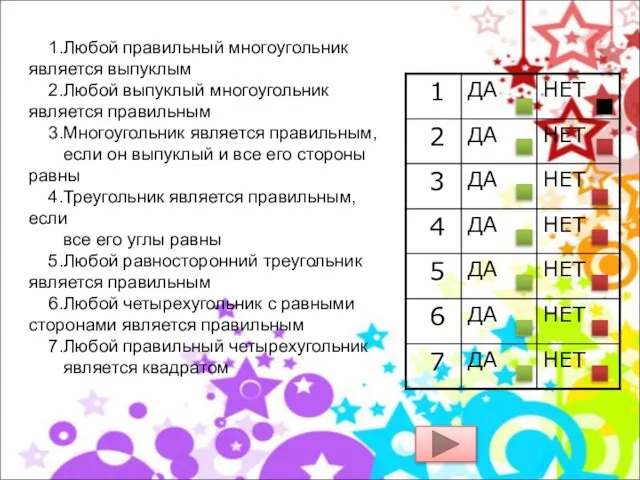
- 18. 1.Любой правильный многоугольник является выпуклым 2.Любой выпуклый многоугольник является правильным 3.Многоугольник является правильным, если он выпуклый
- 19. ПРАВИЛЬНО
- 20. НЕПРАВИЛЬНО
- 22. Скачать презентацию
















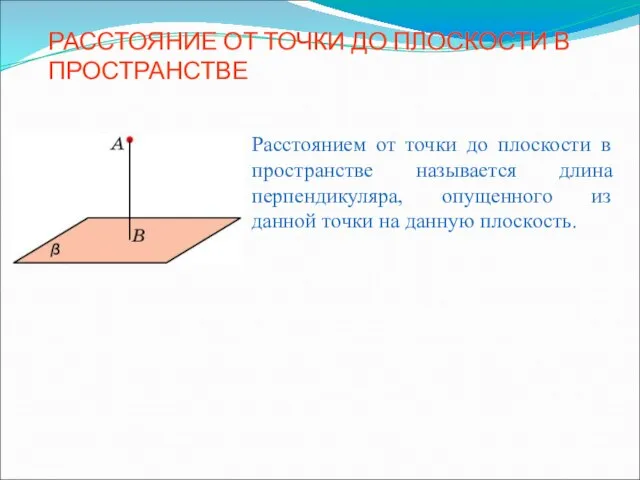 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Правильные многогранники
Правильные многогранники Бозон Хиддинса
Бозон Хиддинса Построение теней
Построение теней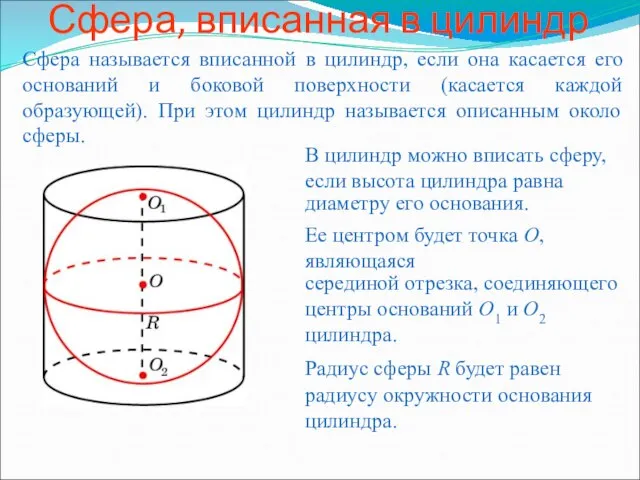 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Задачи на построение сечений в параллелепипеде и тетраэдре
Задачи на построение сечений в параллелепипеде и тетраэдре Треугольники 3 класс
Треугольники 3 класс Шар
Шар Окружности
Окружности Вневписанная окружность треугольника
Вневписанная окружность треугольника В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса  Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Сумма углов в треугольнике
Сумма углов в треугольнике Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Теоремы синусов и косинусов
Теоремы синусов и косинусов Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур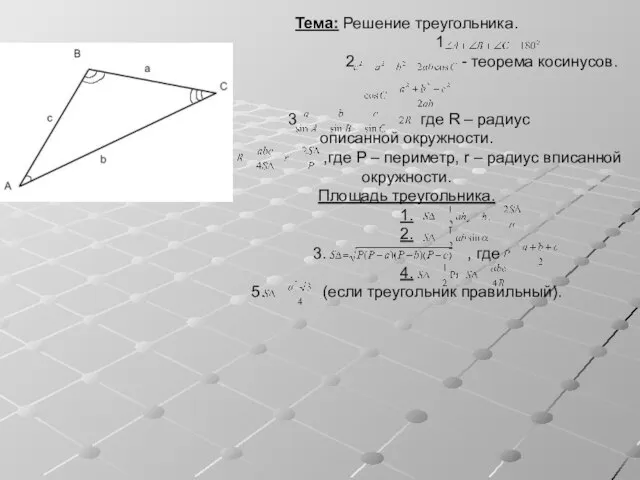 Решение треугольника
Решение треугольника Теорема, обратная теореме Пифагора - презентация по Геометрии_
Теорема, обратная теореме Пифагора - презентация по Геометрии_ Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Координатный метод
Координатный метод Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Преобразование плоскости
Преобразование плоскости Многообразие многоугольников
Многообразие многоугольников Центральная симметрия
Центральная симметрия