Содержание
- 2. Теорема В прямоугольной системе координат скалярное произведение векторов выражается формулой
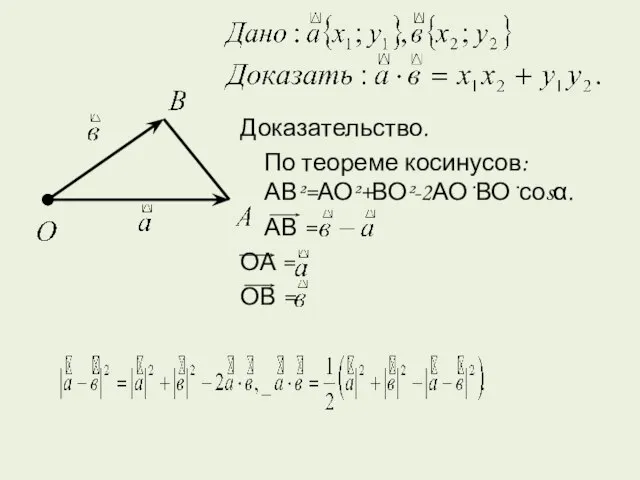
- 3. Доказательство. По теореме косинусов: АВ²=АО²+ВО²-2АО·ВО·соsα. АВ = ОА = ОВ =
- 4. Теорема доказана.
- 5. №1044(а) Дано: Найти: Решение. Ответ: -2,5.
- 6. Следствие 1. Ненулевые векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. №1047(а)
- 7. Следствие 2. Косинус угла между векторами выражается формулой Решение.
- 9. Скачать презентацию

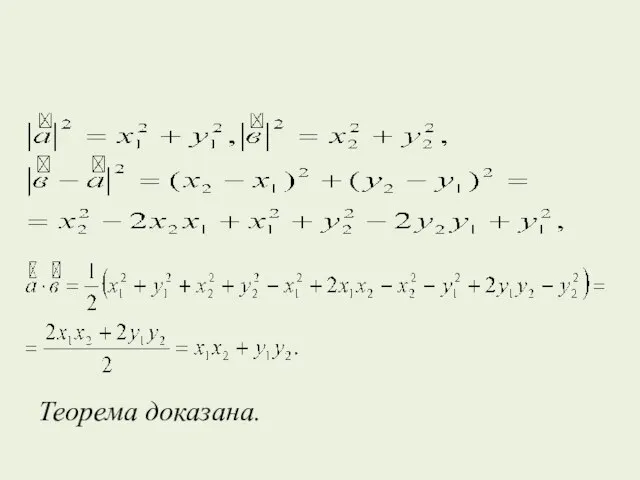



 Понятие объема. Объем призмы
Понятие объема. Объем призмы Векторы
Векторы Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Геометрия. Как она возникла?
Геометрия. Как она возникла? Амидекстр
Амидекстр Тетраэдр и параллепипед
Тетраэдр и параллепипед Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Решение треугольников
Решение треугольников Развитие геометрии
Развитие геометрии ГИА 2013 Модуль «Геометрия» № 11
ГИА 2013 Модуль «Геометрия» № 11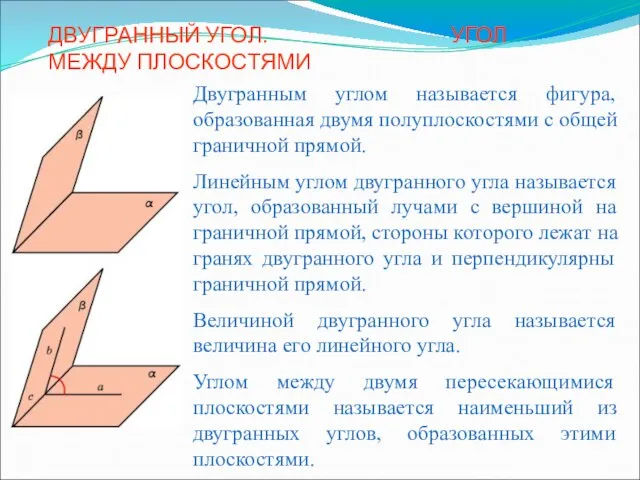 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Площадь круга и его частей
Площадь круга и его частей Луч и угол (7 класс)
Луч и угол (7 класс) От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Понятие многогранника
Понятие многогранника 23.01.13 Классная работа. Длина окружности и площадь круга.
23.01.13 Классная работа. Длина окружности и площадь круга. Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Путешествие в страну Геометрия
Путешествие в страну Геометрия Циклоида
Циклоида Развитие пространственного мышления
Развитие пространственного мышления Теорема о вписанном угле 8 класс - презентация_
Теорема о вписанном угле 8 класс - презентация_ Координатный метод
Координатный метод Идеальные фигуры
Идеальные фигуры Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Треугольники. Третий признак равенства
Треугольники. Третий признак равенства Шар. Сфера
Шар. Сфера Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости