Свойства производной. Построение графиков функций. (Повторение материала 10 класса).

Построение графика функции, заданной формулой, начинают с её исследования
1) Находят область определения функции
2) Выясняют, является ли функция четной (или нечетной), является ли периодической
3) Находят точки пересечения функции с осями ОХ и ОУ
4) Находят промежутки знакопостоянства функции
5) Находят промежутки возрастания и убывания
6) Точки экстремума и значения функции в этих точках
7) Исследуют поведение функции в «особых» точках и при больших х (проверяют на асимптоты)

Промежутки возрастания и убывания (промежутки монотонности).
Достаточный признак убывания :
если f’ (x)< 0, то f (x) убывает на данном промежутке.
Достаточный признак возрастания : если f’ (x)> 0, то f (x) возрастает на данном промежутке.

Пример.
Для функции
найти промежутки монотонности.
D(f)=( –∞; +∞), функция непрерывна и
дифференируема на области определения.
2.
если 4х³ –16х = 0;
4х(х–2)(х+2) = 0;
х = –2; х =2.

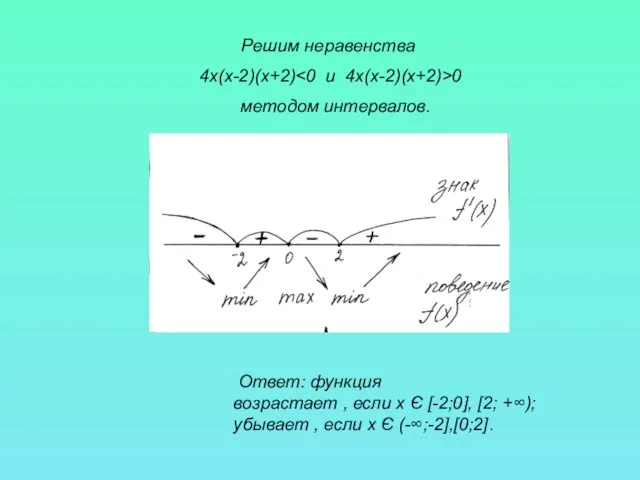
Решим неравенства
4х(х-2)(х+2)<0 и 4х(х-2)(х+2)>0
методом интервалов.
Ответ: функция
возрастает , если х Є [-2;0], [2; +∞);
убывает , если х Є (-∞;-2],[0;2].

Точки экстремума функции
(точки максимума и точки минимума)
Точка a называется точкой максимума функции f(x), если верно неравенство f(x)≤f(a)
Если при переходе через точку a производная меняет знак с «+» на «-»,
то эта точка является
точкой максимума

Точки экстремума функции
(точки максимума и точки минимума)
Точка a называется точкой минимума функции f(x), если верно неравенство
f(x) ≥f(a)
Если при переходе через точку a производная меняет знак с «-» на «+»,
то эта точка является
точкой минимума

Если производная сохраняет свой знак при переходе через точку a, то такая точка называется точкой перегиба

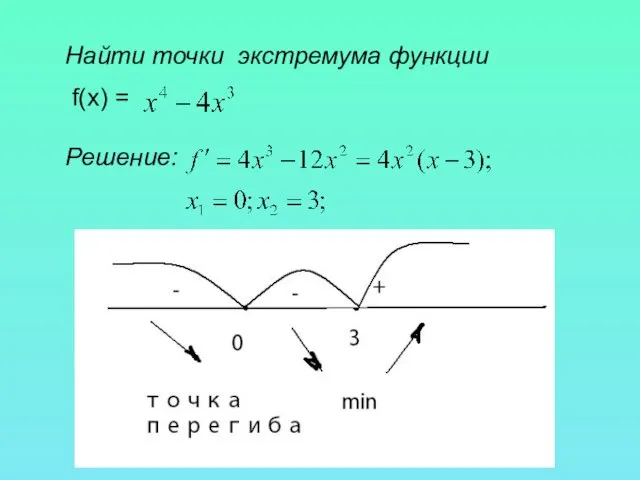
Найти точки экстремума функции
f(x) =
Решение:

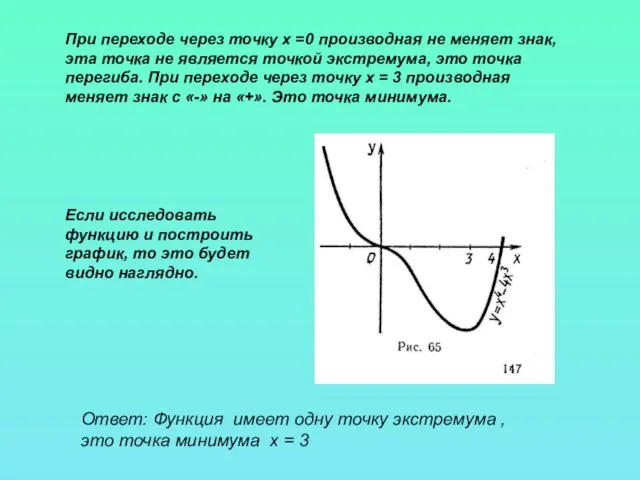
Ответ: Функция имеет одну точку экстремума , это точка минимума х = 3
При переходе через точку х =0 производная не меняет знак, эта точка не является точкой экстремума, это точка перегиба. При переходе через точку х = 3 производная меняет знак с «-» на «+». Это точка минимума.
Если исследовать функцию и построить график, то это будет видно наглядно.

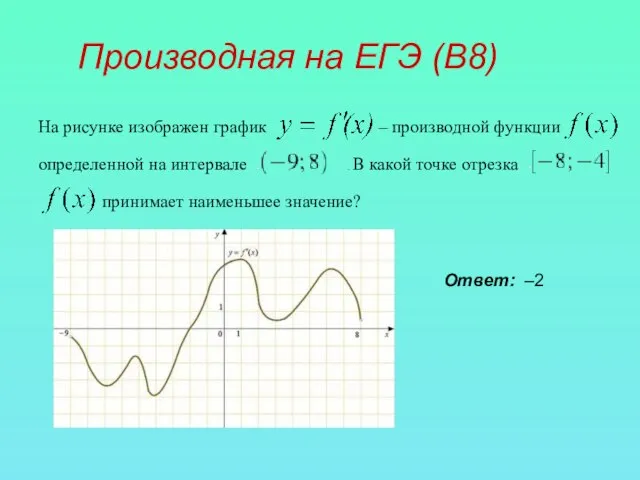
Производная на ЕГЭ (В8)
На рисунке изображен график
– производной функции
определенной на интервале
. В какой точке отрезка
принимает наименьшее значение?
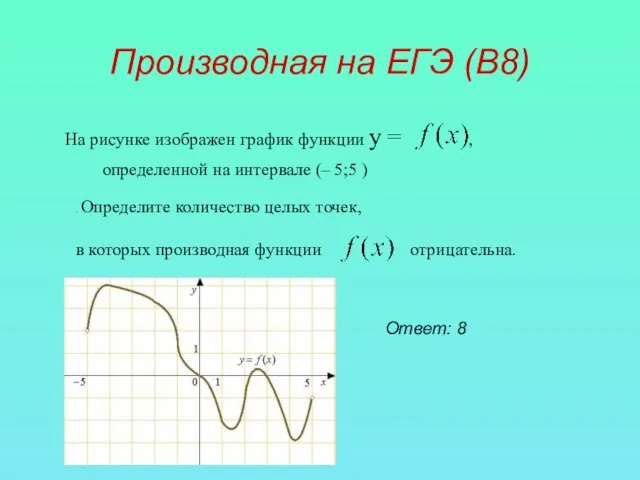
Ответ: –2

Производная на ЕГЭ (В8)
На рисунке изображен график функции у = ,
определенной на интервале (– 5;5 )
. Определите количество целых точек,
в которых производная функции отрицательна.
Ответ: 8

Производная на ЕГЭ (В14)
Найдите наименьшее значение функции у = х³ + 6х² +9х + 24
на отрезке [ - 2; - 0,5 ]
Решение. 3х² +12х + 9
3х² +12х + 9 = 0 х = –3; х = –1
3(х+3)(х+1)<0 и 3(х+3)(х+1)>0
Знаки производной
< 0 на [–3; –1] и
> 0 на (–∞;–3], [–1;+ ∞)
х= –1 точка минимума
Ответ: 20

Использованные ресурсы:
Открытый банк задач ЕГЭ по математике 2012
http://live.mephist.ru/show/mathege2010/
Обучающая система Д. Гущина «РЕШУ ЕГЭ»
http://reshuege.ru/
Мордкович А.П. П.В. Алгебра и начала анализа (профильный уровень) 10 класс, М., «Мнемозина», 2006.
Алимов Ш.А.Алгебра и начала анализа 10-11 класс, М., «Просвещение»,1999.