Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________
Содержание
- 2. Дорогу осилит идущий, а математику – мыслящий Т.Эдисон Цель урока Изучить способ построения графиков функций y
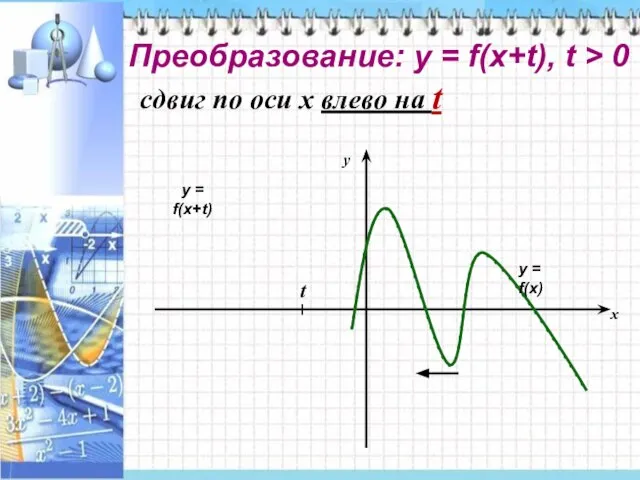
- 3. Преобразование: у = f(x+t), t > 0 сдвиг по оси x влево на t t у
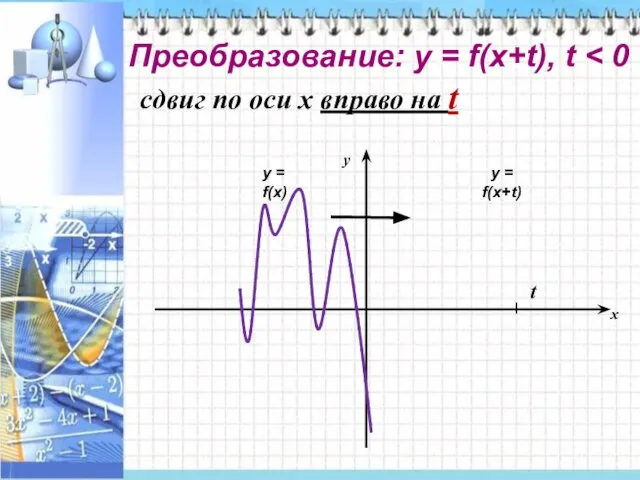
- 4. Преобразование: у = f(x+t), t сдвиг по оси x вправо на t t у = f(x)
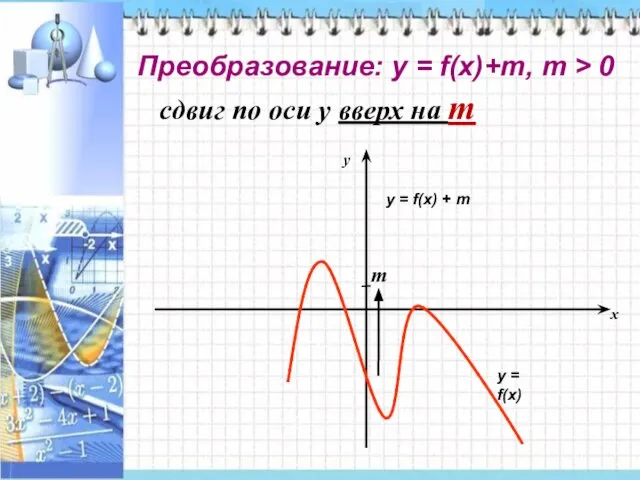
- 5. Преобразование: у = f(x)+m, m > 0 сдвиг по оси у вверх на m m у
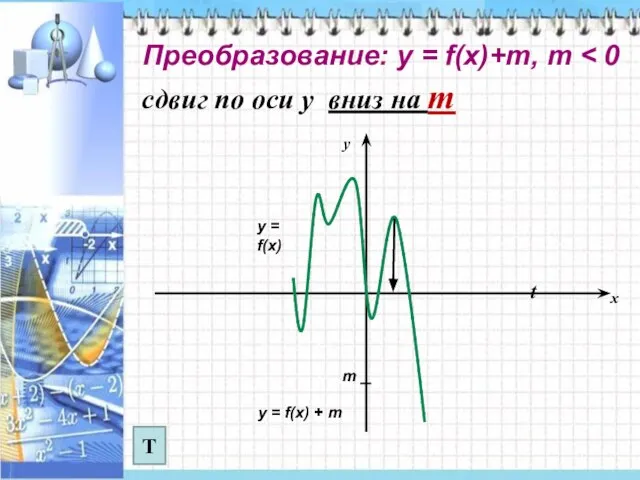
- 6. сдвиг по оси у вниз на m t у = f(x) у = f(x) + m
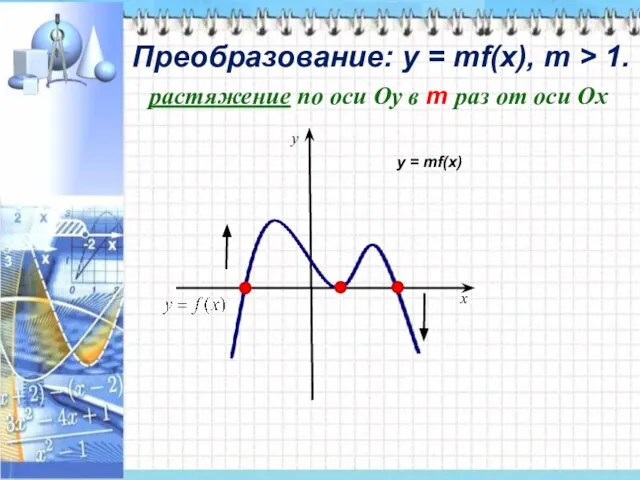
- 7. Преобразование: у = mf(x), m > 1. x y растяжение по оси Оу в m раз
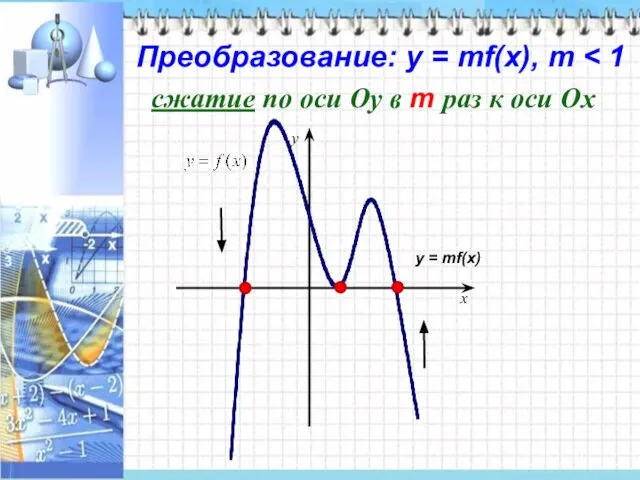
- 8. x y у = mf(x) Преобразование: у = mf(x), m сжатие по оси Оу в m
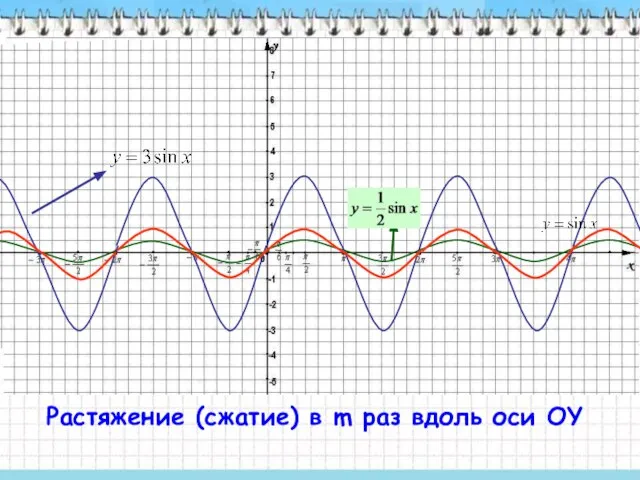
- 9. Растяжение (сжатие) в m раз вдоль оси OY
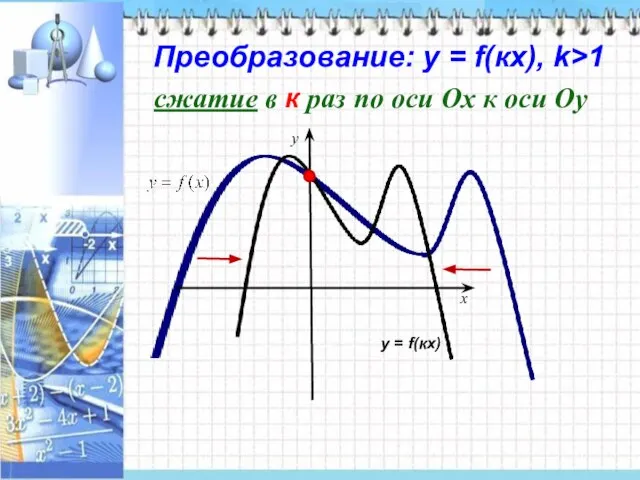
- 10. Преобразование: у = f(кx), k>1 x y сжатие в к раз по оси Ох к оси
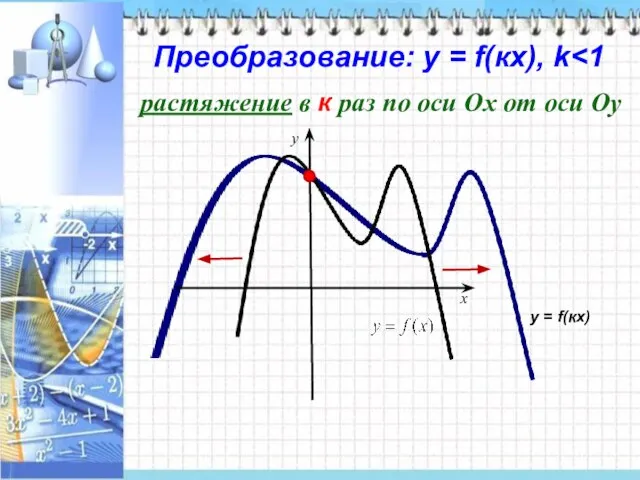
- 11. Преобразование: у = f(кx), k x y растяжение в к раз по оси Ох от оси
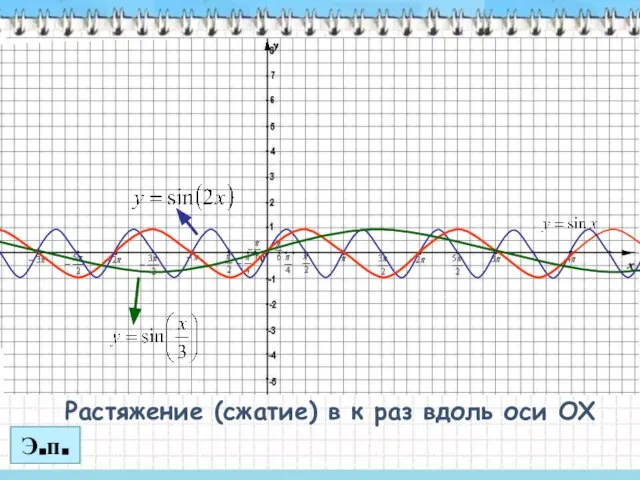
- 12. Растяжение (сжатие) в к раз вдоль оси OX Э.п.
- 13. Постройте графики функций 1 ряд 3 ряд 2 ряд На доске
- 14. Домашняя работа: §§ 12 – 13, доработать опорный конспект, № 230(в); 239(в); 240(в); 242(в).
- 16. Скачать презентацию



 Построение геометрических тел
Построение геометрических тел Понятие многогранника
Понятие многогранника Треугольники 3 класс
Треугольники 3 класс Правильные фигуры и тела
Правильные фигуры и тела Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Упражнения со спичками (занятие 9)
Упражнения со спичками (занятие 9) Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д.
Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д. Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Смотр общественных знаний
Смотр общественных знаний Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Геометрия 10 класс - презентация по Геометрии
Геометрия 10 класс - презентация по Геометрии Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Четырехугольники 9 класс
Четырехугольники 9 класс Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Измерение углов
Измерение углов вид разреза сечения
вид разреза сечения Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Флексагоны
Флексагоны Приготовьтесь к построению!
Приготовьтесь к построению! Понятие цилиндра
Понятие цилиндра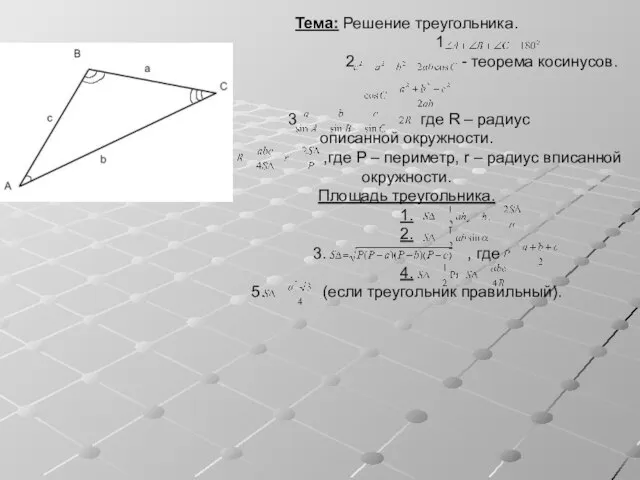 Решение треугольника
Решение треугольника Длина окружности. Площадь круга
Длина окружности. Площадь круга Объём пирамиды
Объём пирамиды Призма 9 класс
Призма 9 класс Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах.