Элементы алгебры логики. Высказывание. Математические основы информатики

Элементы алгебры логики. Высказывание
Алгебра логики.
Логические переменные.
1
2
Логические значения.
3

Раздел математики

Раздел математики
Алгебраическое уравнение

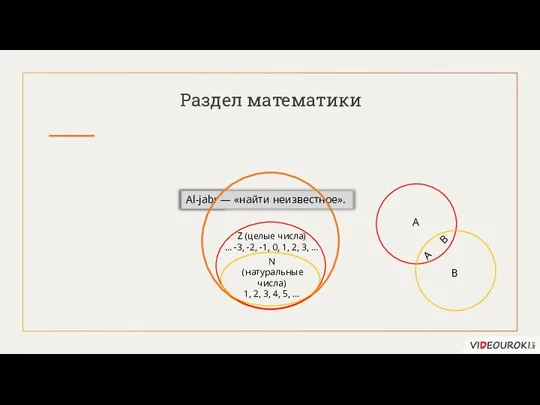
Al-jabr
Раздел математики
Al-jabr — «найти неизвестное».
N
(натуральные числа)
1, 2, 3, 4, 5, …
Z (целые числа)
… -3, -2, -1, 0, 1, 2, 3, …
А
В

Раздел математики
Алгебра
логики
Алгебра
чисел
Алгебра
множеств

Раздел математической логики
=
=
Лампочка горит.
Истинно.
Ложно.

Алгебра логики
Высказывание — это предложение на любом языке, содержание которого можно
однозначно определить как истинное или ложное.
Москва — столица России.
Шесть минус два равно четыре.

Алгебра логики
Высказывание — это предложение на любом языке, содержание которого можно
однозначно определить как истинное или ложное.
Зайцы зимой впадают в спячку.

Алгебра логики
Высказывание — это предложение на любом языке, содержание которого можно
однозначно определить как истинное или ложное.
Зайцы зимой впадают в спячку.
Москва — столица России.
Шесть минус два равно четыре.
Высказывания

Высказывание
В естественных языках высказывания выражаются с помощью повествовательных
предложений, но не все повествовательные предложения являются высказываниями.

Высказывание
Если попасть камнем в окно, то оно разобьётся.
В естественных языках высказывания выражаются с помощью повествовательных
предложений, но не все повествовательные предложения являются высказываниями.

В естественных языках высказывания выражаются с помощью повествовательных
предложений, но не все повествовательные предложения являются высказываниями.
Физическая культура — самый важный школьный предмет.
Высказывание
Физическая культура является очень полезным уроком.

Высказываниями не являются побудительные и вопросительные предложения.
Сколько времени?
Чей телефон звонит на уроке?
Сколько тебя можно ждать!
Высказывание

Для построения высказываний могут использоваться знаки различных формальных
языков: математики, физики, химии и др.
Высказывание

Для построения высказываний могут использоваться знаки различных формальных
языков: математики, физики, химии и др.
S
Высказывание

Числовые выражения не являются высказываниями.
Но если из двух выражений составить одно и соединить их знаком равенства или
неравенства, то новое выражение будет высказыванием.
Высказывание

Равенства или неравенства, которые содержат в себе переменные, не относятся
к высказываниям.
Высказывание
Не является высказыванием.
Если переменные в неравенстве заменить цифрами, то есть конкретными
значениями, то оно становится высказыванием, т. к. переменные были заменены
конкретными значениями.
Является высказыванием.

Равенства или неравенства, которые содержат в себе переменные, не относятся
к высказываниям.
Если переменные в неравенстве заменить цифрами, то есть конкретными значениями, то оно становится высказыванием, т. к. переменные были заменены конкретными значениями.
Высказывание

Истинно или ложно то или иное высказывание, решается, исходя из тех наук,
к которым оно относится.
Высказывание
Математика

Важным фактором для алгебры логики является не содержание высказываний,
а истинно или ложно то или иное высказывание.
Высказывание
Высказывания обозначаются при помощи букв.
Такие обозначения называются логическими переменными.
А
В
Если высказывание истинно, то значение соответствующей логической переменной
обозначается единицей, а если ложно — нулём.
Логические
значения

Определяет правила записи, упрощения и преобразования высказываний и
вычисления их значений.
Алгебра логики
Производя операции с логическими переменными, которые могут быть равны
только 0 или 1, с помощью алгебры логики можно свести обработку информации к
операциям с двоичными данными.

Аппарат алгебры логики