Содержание
- 2. § 6. Векторы. Линейные операции на множестве векторов 1. Основные понятия ОПР. Вектором называется направленный отрезок
- 3. Расстояние от начала вектора до его конца называется длиной (или модулем) вектора. Вектор, длина которого равна
- 4. Два вектора ā и b̄ называются равными, если они сонаправлены и имеют одинаковую длину. ā =
- 5. 2. Линейные операции на множестве векторов Умножение на число; 2) Сложение векторов ОПР. Произведением вектора ā
- 6. ОПР. (сложение - правило треугольника). Пусть даны два вектора ā и b̄ . Поместим начало b̄
- 7. ОПР. (правило параллелограмма). Пусть даны два вектора ā и b̄ . Совместим их начала, построим на
- 8. СВОЙСТВА ЛИНЕЙНЫХ ОПЕРАЦИЙ НАД ВЕКТОРАМИ 1) ā + b̄ = b̄ + ā (коммутативность сложения векторов);
- 9. 3. Проекция вектора ОПР. Прямую, на которой выбрано направление, называют осью. Пусть ℓ – ось, –
- 10. 4. Понятия линейной зависимости и независимости. Базис ОПР. Говорят, что векторы ā1, ā2, …, āk линейно
- 11. Пусть V(3)– множество свободных векторов пространства (V(2) - плоскости). ОПР. Совокупность любых двух линейно независимых векторов,
- 12. Системы координат. ОПР. Осью называется прямая с выбранным на ней направлением. ОПР. Афинной системой координат (косоугольной
- 13. ТЕОРЕМА 4 (о базисе). Каждый вектор множества V(3) (V(2)) линейно выражается через любой его базис ,
- 14. ТЕОРЕМА 5 (основная теор. векторной алгебры). Пусть {α1, α2, α3} – координаты вектора ā в базисе
- 15. ТЕОРЕМА 6 (критерий коллинеарности свободных векторов в координатной форме). Векторы ā = {α1 ; α2 ;
- 16. Матрица перехода Рассмотрим два базиса векторного пространства V(3) Е = {ēi} = и F = {f̅i}
- 18. Скачать презентацию














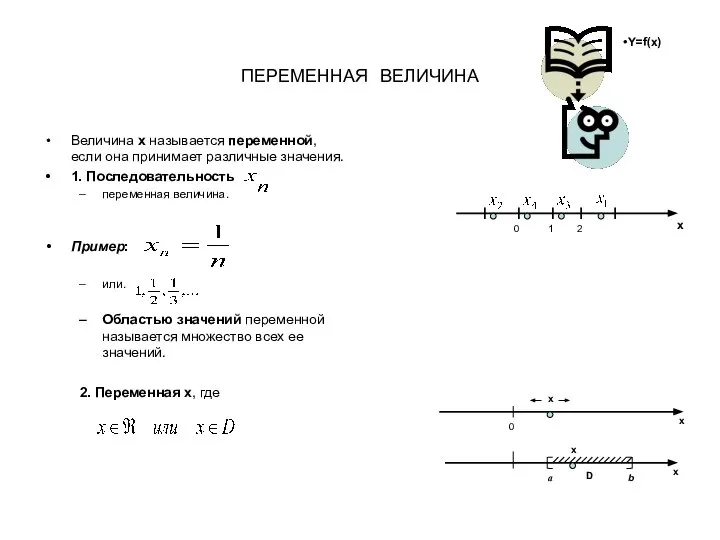 Переменная величина
Переменная величина Квадратный корень
Квадратный корень Соответствия величин вычисления. 11 класс, 9 задание
Соответствия величин вычисления. 11 класс, 9 задание Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2
Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2 Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс)  Л 5 Функция одной переменной
Л 5 Функция одной переменной Понятие ”тетраэдр”
Понятие ”тетраэдр” Графы и их применение при решении задач
Графы и их применение при решении задач Аксиомы стереометрии
Аксиомы стереометрии Теория графов. Основные понятия
Теория графов. Основные понятия Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Линейные неравенства с параметром
Линейные неравенства с параметром Решение задач
Решение задач Визуализация операций над эллиптическими кривыми
Визуализация операций над эллиптическими кривыми Область определения функции
Область определения функции Свойства алгоритма
Свойства алгоритма Движение по окружности
Движение по окружности Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Типы задач на проценты
Типы задач на проценты Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Измеряй и сравнивай
Измеряй и сравнивай Тела вращения. Открытый урок
Тела вращения. Открытый урок Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника 3.3. Понятие функции
3.3. Понятие функции Как помочь ребенку понять математику. Вебинар 2
Как помочь ребенку понять математику. Вебинар 2 Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных
Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных Theorem of rational root with integral coefficients
Theorem of rational root with integral coefficients