Геометрический и механический смысл производной

Цели урока:
Проверить усвоение стандартного материала каждым учеником и оказание помощи учащимся по ликвидации пробелов в процессе личного общения на уроке;
Учить применять знания при решении базовых и нестандартных задач;
Показать широкий спектр применения производной.

.
3) y=tgx-ctgx
1) у=-7х
5) у=πх-2 соs3x
7) у=(6- 3х )²
Устная работа
Найти производную.

Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Геометрический смысл
производной.

Задания из ЕГЭ

3
Ответ: -0,25
Задание №1.На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х0
.Найдите значение производной функции f(x) в точке х0.
У=f(x)

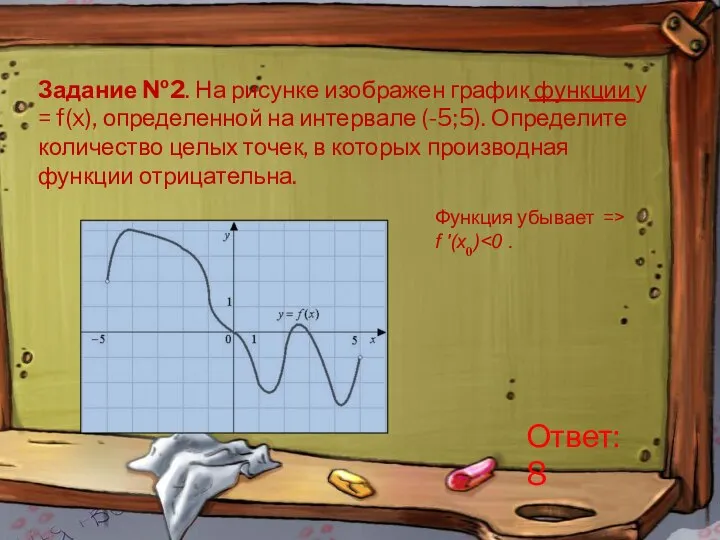
Задание №2. На рисунке изображен график функции у = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
Ответ: 8
Функция убывает =>
f '(x0)<0 .

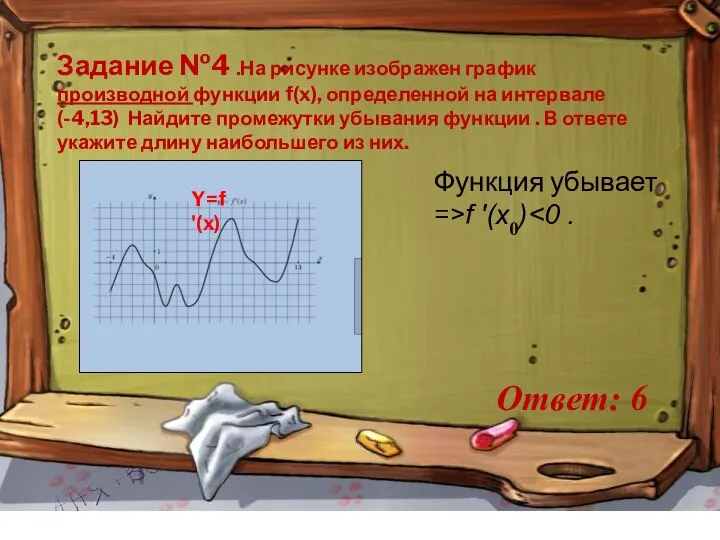
Задание №4 .На рисунке изображен график производной функции f(x), определенной на интервале (-4,13) Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.
Функция убывает =>f '(x0)<0 .
Ответ: 6
Y=f '(x)

44
Задание №3.На рисунке изображен график производной функции f'(x), определенной на интервале (-9;8). Найдите точку экстремума функции на интервале (-3;3).
Ответ: - 2
Y=f(x)

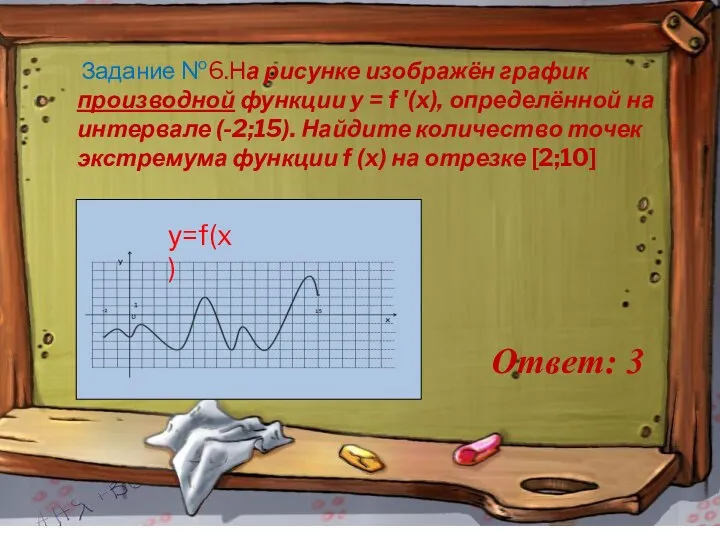
Задание №6.На рисунке изображён график производной функции y = f '(x), определённой на интервале (-2;15). Найдите количество точек экстремума функции f (x) на отрезке [2;10]
Ответ: 3
у=f(x)

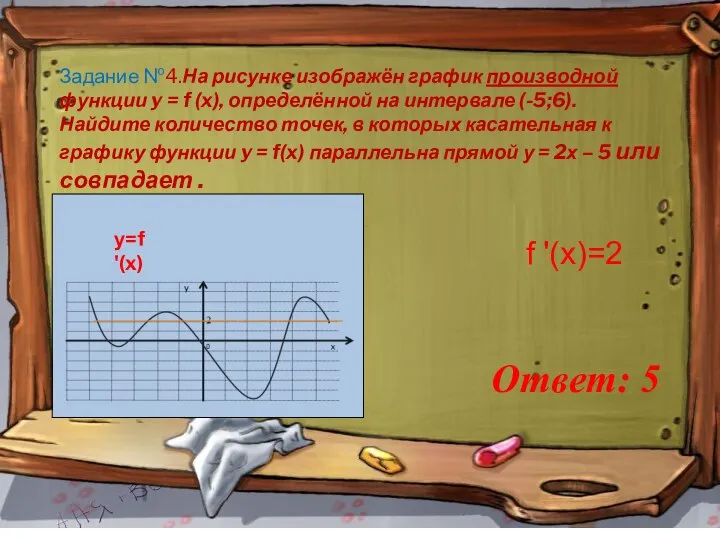
Задание №4.На рисунке изображён график производной функции y = f (x), определённой на интервале (-5;6). Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой у = 2х – 5 или совпадает .
Ответ: 5
f '(х)=2
у=f '(x)

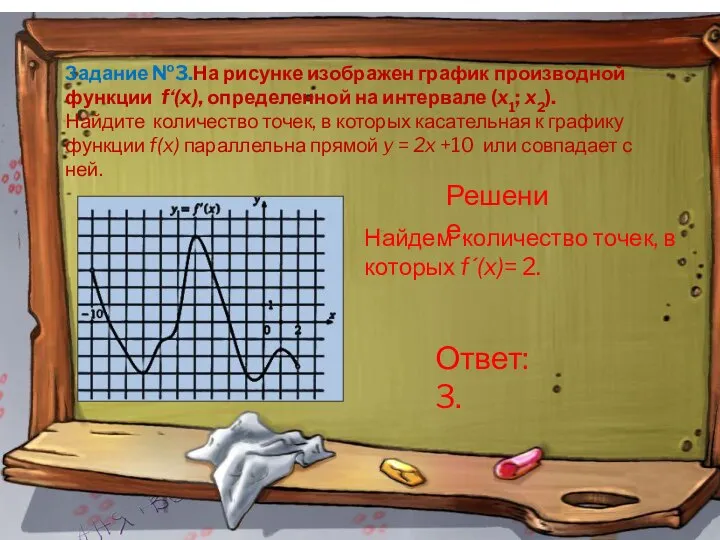
Задание №3.На рисунке изображен график производной функции f‘(x), определенной на интервале (x1; x2).
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x +10 или совпадает с ней.
Найдем количество точек, в которых f´(x)= 2.
Решение.
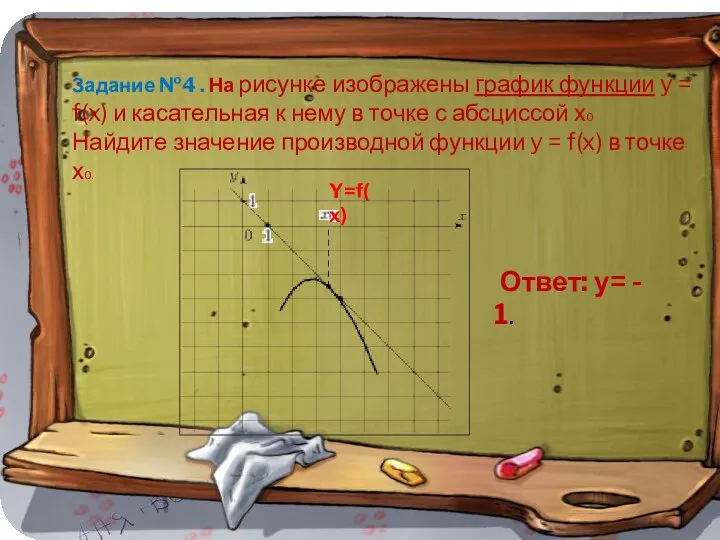
Ответ:3.

Задание №4 . На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0 Найдите значение производной функции y = f(x) в точке х0.
Ответ: у= - 1.
Y=f(x)

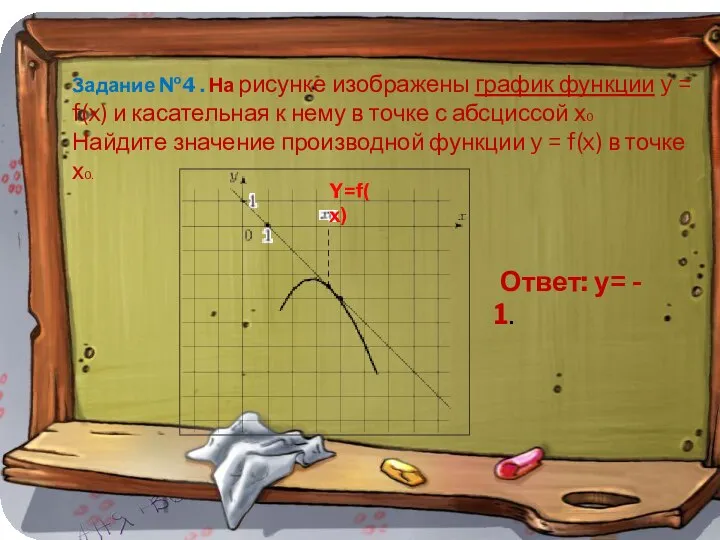
Задание №4 . На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0 Найдите значение производной функции y = f(x) в точке х0.
Ответ: у= - 1.
Y=f(x)

Механический смысл
производной.

Алгоритм нахождения производной в физике и технике:
Находим производную от координаты по времени (она равна скорости)
Найдём производную скорости от времени (она равна ускорению)
Производная в физике и технике
Производная от координаты по времени есть скорость.
В этом заключается механический смысл производной x'(t)=u(t)
Производная от скорости по времени есть ускорение u'(t)=a
Производная в физике и технике.

Задача №2. Лыжник, спускаясь с горы, движется по закону
s(t) = 0,5t² - t. Найти скорость и ускорение лыжника в момент времени t= 3 с, если расстояние измеряется в метрах. Какое это движение?
Решите задачи.

Задание на самоподготовку: §28-29
№ 28.29(в,г);28.32(г);28.38(а);29.21(в,г),
:
Тяжело в учении легко в бою !
Учебник :
Математика. 10класс. А.Г.Мордкович и др. – М. :Мнемозина, 2009.