Содержание
- 2. Геометрия Планиметрия Стереометрия stereos телесный, твердый, объемный, пространственный
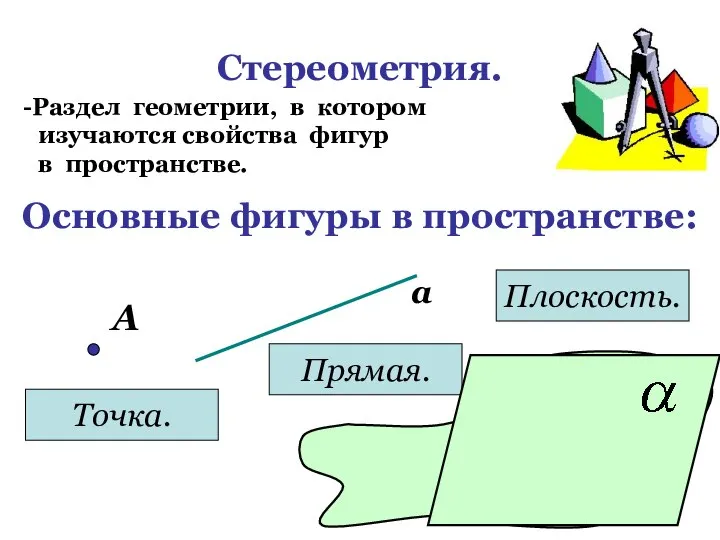
- 3. Стереометрия. Раздел геометрии, в котором изучаются свойства фигур в пространстве. Основные фигуры в пространстве: А Точка.
- 4. A, B, C, … a, b, c, … или AВ, BС, CD, …
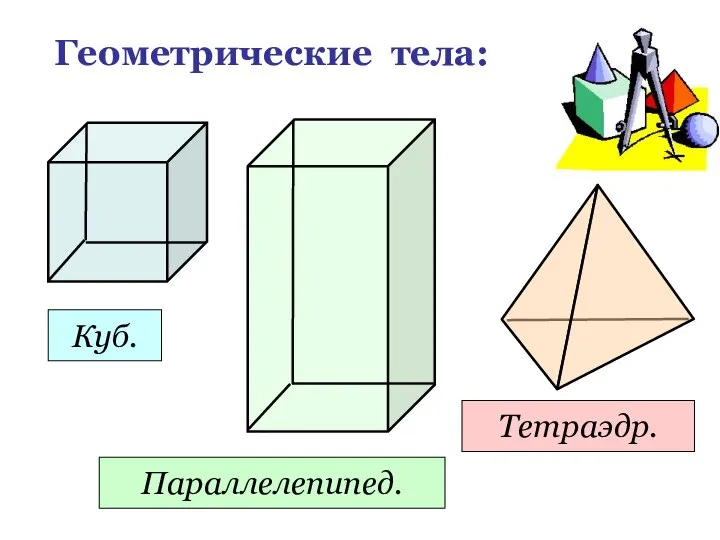
- 5. Геометрические тела: Куб. Параллелепипед. Тетраэдр.
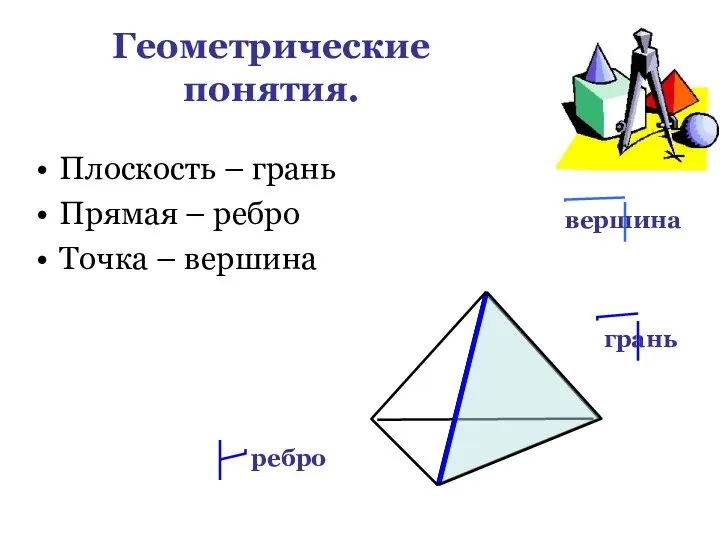
- 6. Геометрические понятия. Плоскость – грань Прямая – ребро Точка – вершина вершина грань ребро
- 7. Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства
- 8. АКСИОМЫ планиметрия стереометрия 1. Каждой прямой принадлежат по крайней мере две точки 2. Имеются по крайней
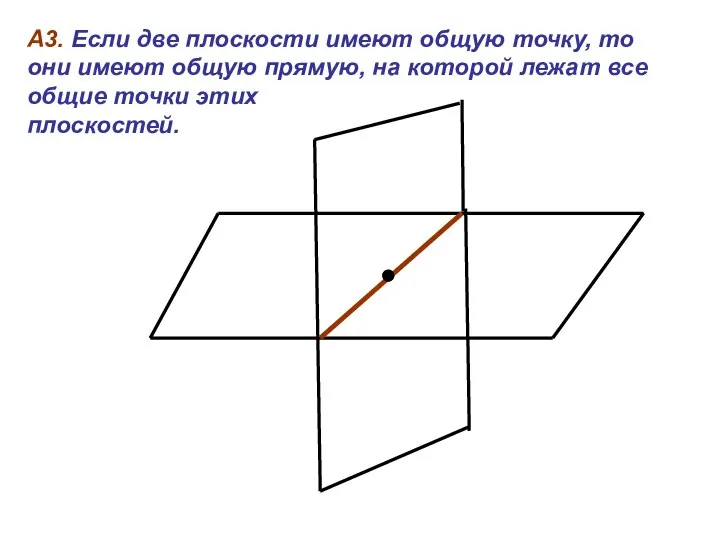
- 9. А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все
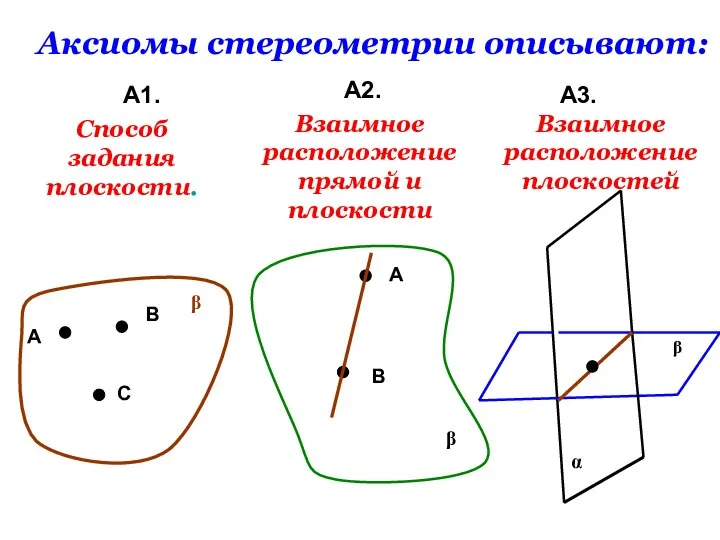
- 10. Аксиомы стереометрии описывают: А1. А2. А3. А В С β Способ задания плоскости. β А В
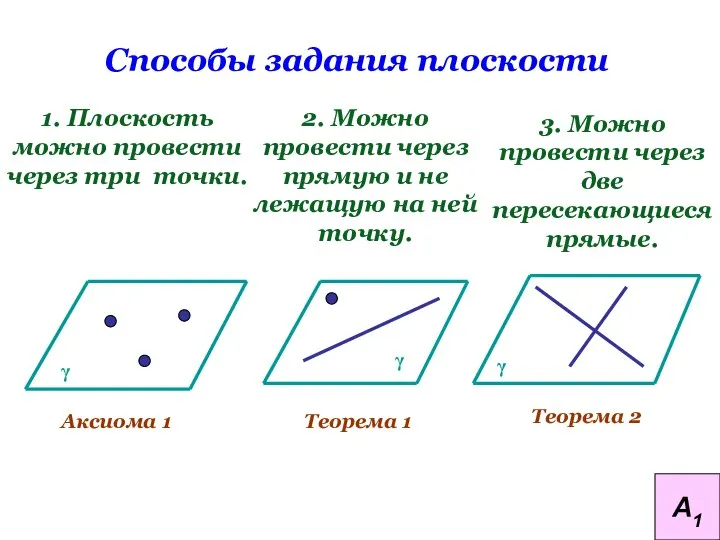
- 11. Способы задания плоскости 1. Плоскость можно провести через три точки. 2. Можно провести через прямую и
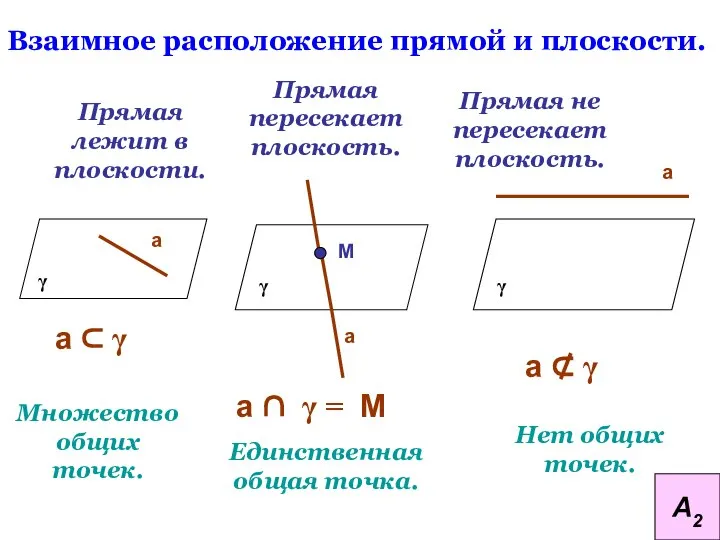
- 12. Взаимное расположение прямой и плоскости. Прямая лежит в плоскости. Прямая пересекает плоскость. Прямая не пересекает плоскость.
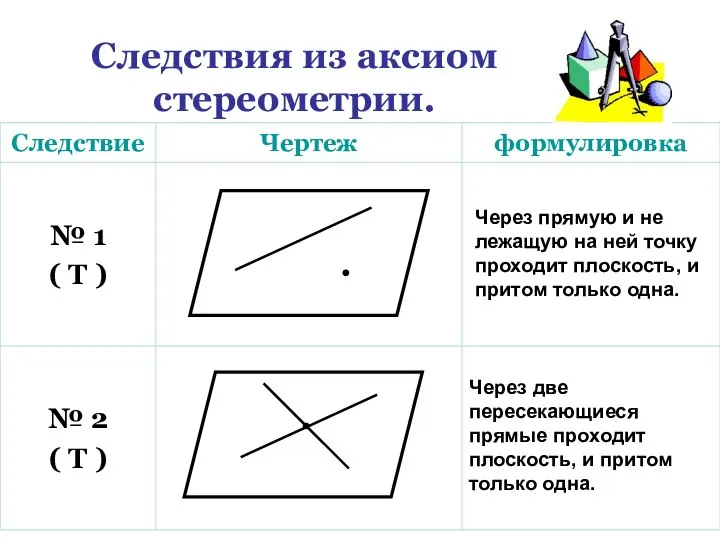
- 13. Следствия из аксиом стереометрии. Через прямую и не лежащую на ней точку проходит плоскость, и притом
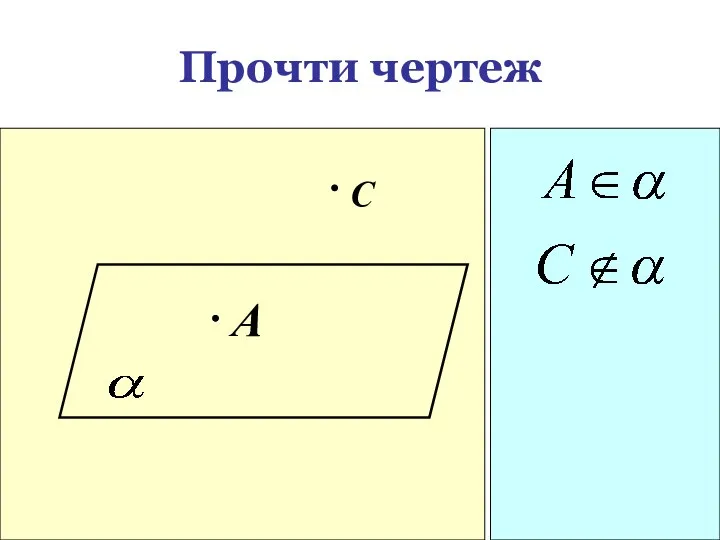
- 14. Прочти чертеж A С
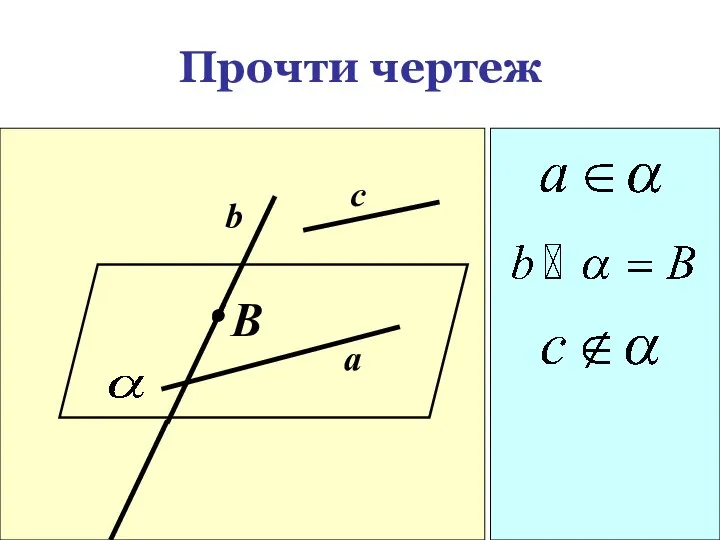
- 15. Прочти чертеж B c b a
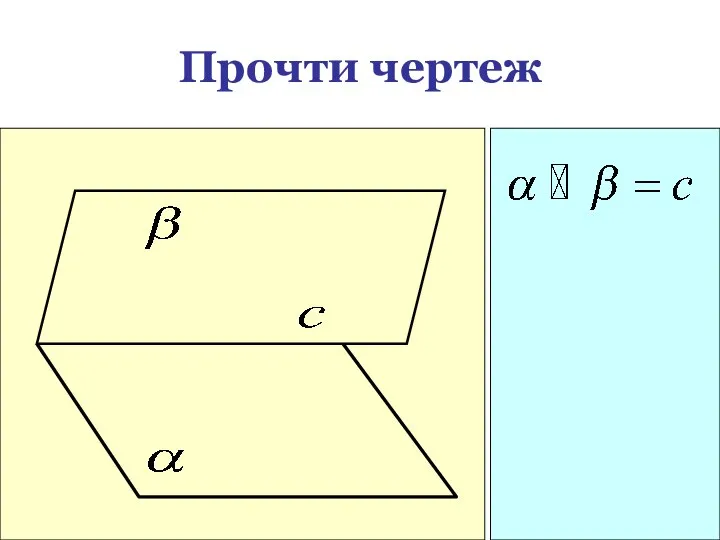
- 16. Прочти чертеж
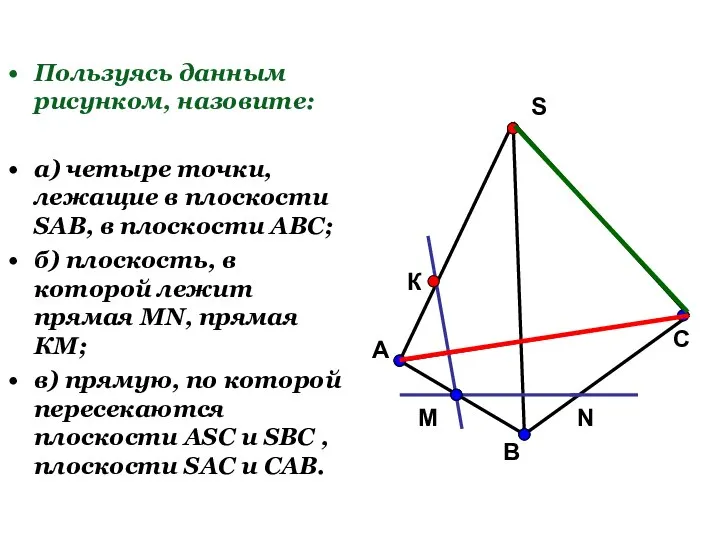
- 17. Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость,
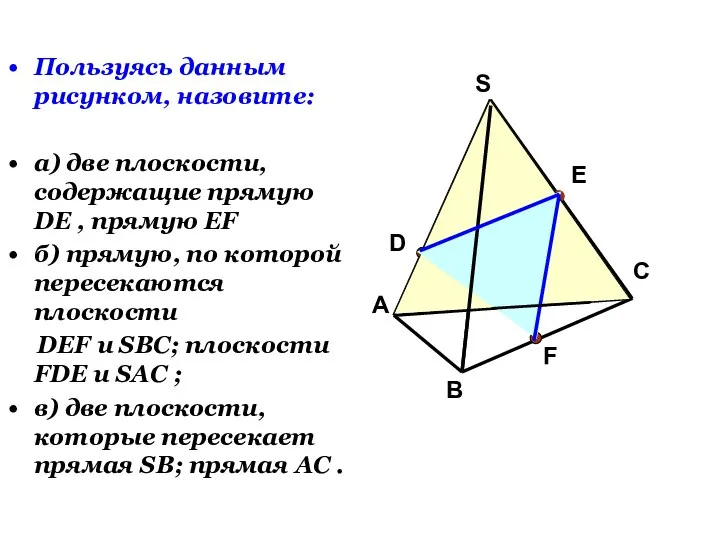
- 18. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE , прямую EF б) прямую, по
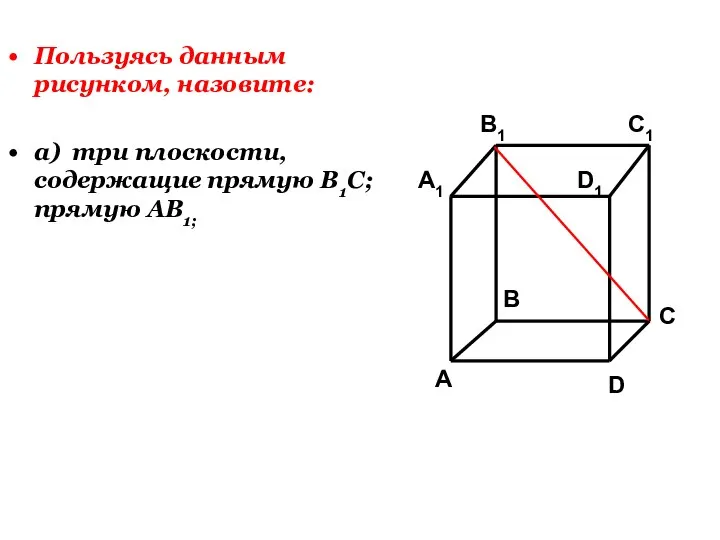
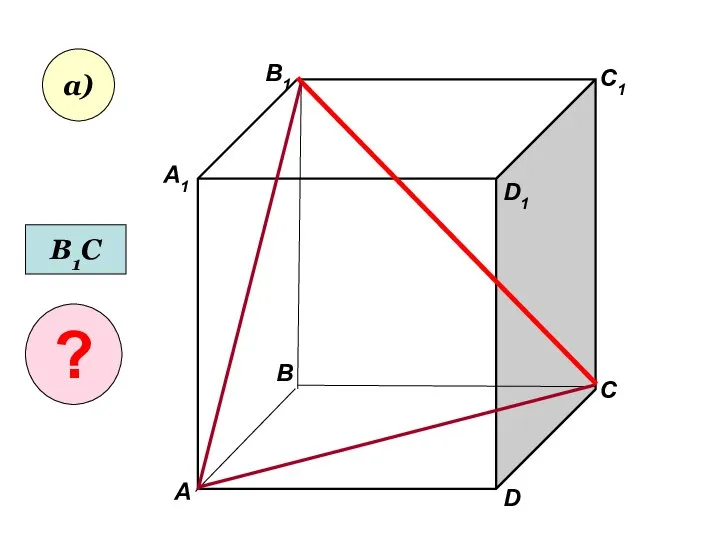
- 19. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1;
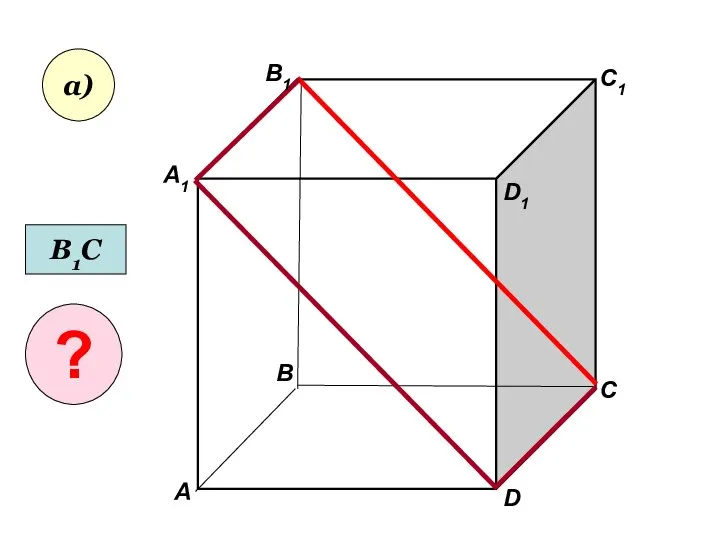
- 20. А А1 В В1 С D1 D C1 а) В1С ?
- 21. А А1 В В1 С D1 D C1 а) В1С ?
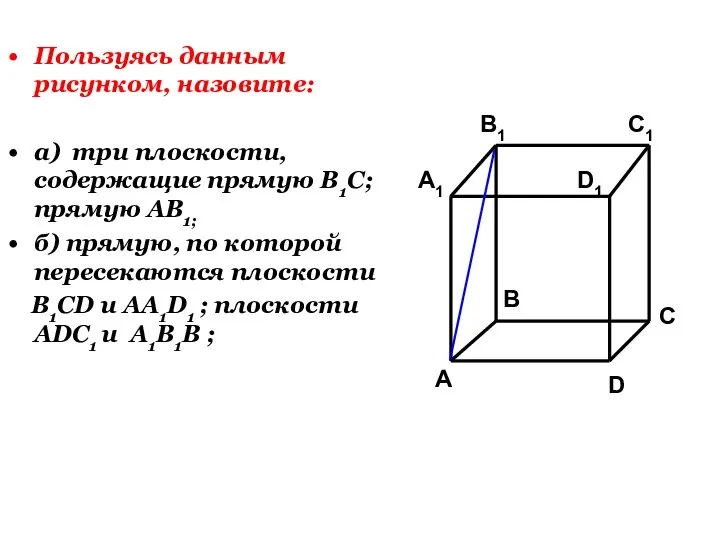
- 22. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 23. А А1 В В1 С D1 D C1 б)
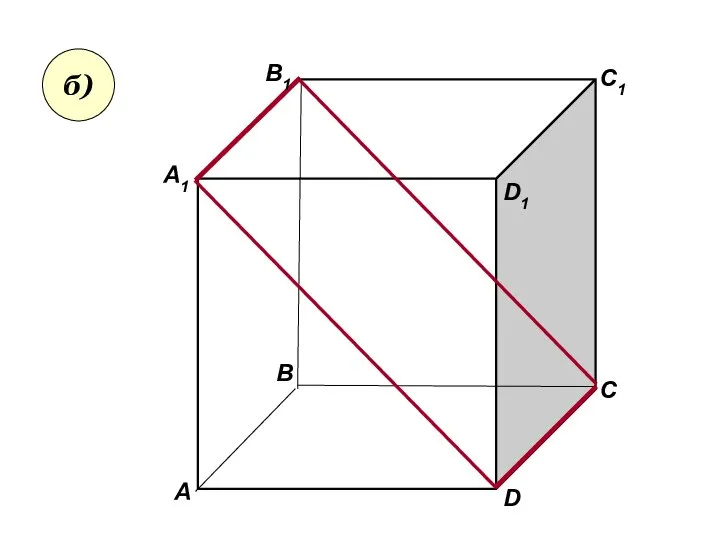
- 24. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
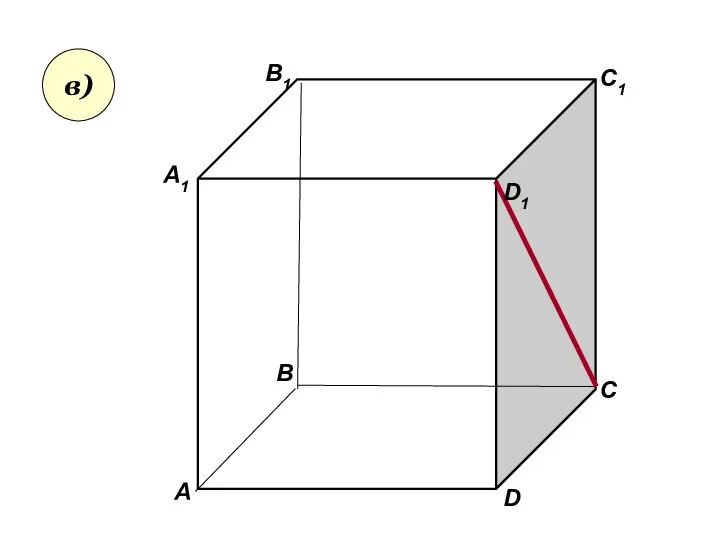
- 25. А А1 В В1 С D1 D C1 в)
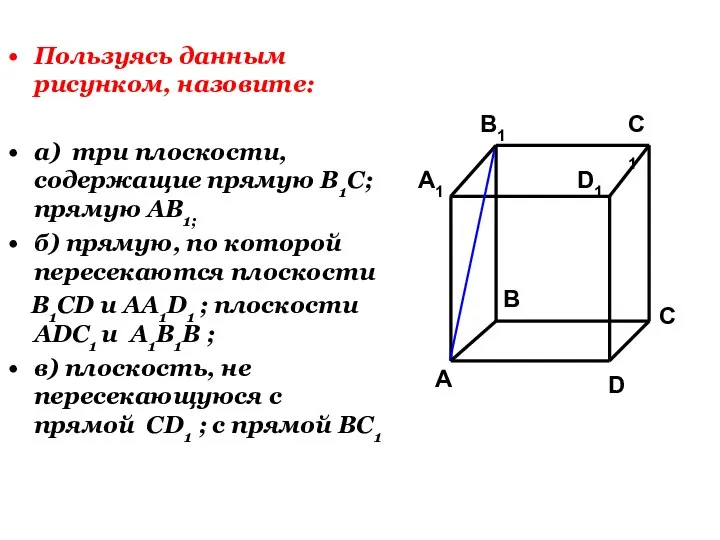
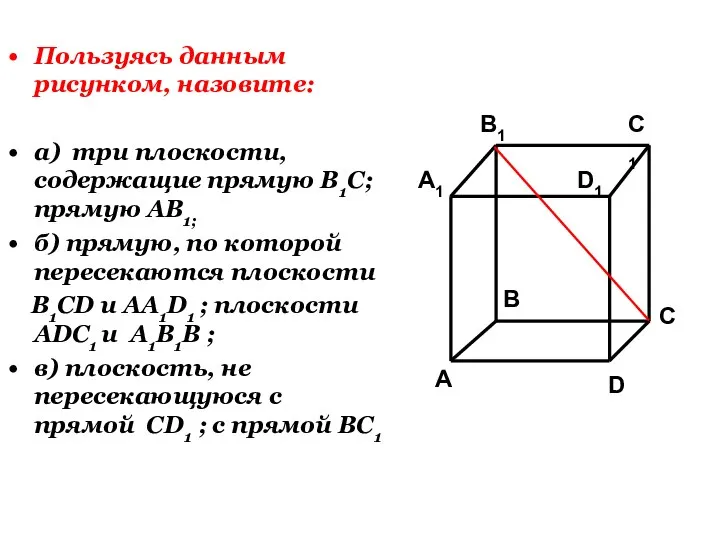
- 26. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 28. Скачать презентацию



 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Тест. Равенство треугольников
Тест. Равенство треугольников Логарифм числа
Логарифм числа Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сложение с числом 10
Сложение с числом 10 Линейная корреляция
Линейная корреляция Проецирование – это процесс получения
Проецирование – это процесс получения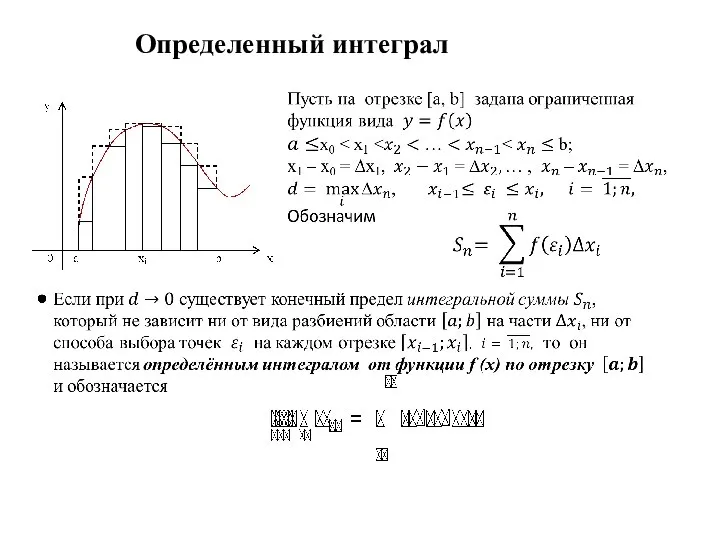 Определённый интеграл
Определённый интеграл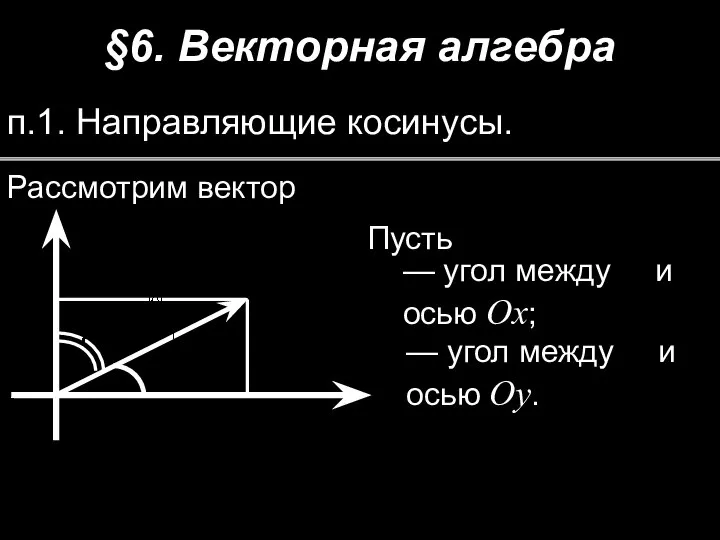 2.3. Векторная алгебра
2.3. Векторная алгебра Признаки параллельности прямых
Признаки параллельности прямых Решение задач. Урок математики
Решение задач. Урок математики Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Подготовка к ЕГЭ
Подготовка к ЕГЭ Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Лекция 5. Трехмерные преобразования
Лекция 5. Трехмерные преобразования Кратные чисел. 5 класс
Кратные чисел. 5 класс 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Pervoobraznaya
Pervoobraznaya Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм Решение треугольников
Решение треугольников Треугольник. Виды треугольников
Треугольник. Виды треугольников Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Иррациональные числа
Иррациональные числа Тест 3 по математике
Тест 3 по математике