Содержание
- 2. - это задача, для которой невозможно построить алгоритм решения. Алгоритмически неразрешимая задача
- 3. В 1900 г. на Международном математическом конгрессе в Париже немецкий математик Д.Гильберт сформулировал 23 математические проблемы.
- 4. Задано произвольное алгебраическое уравнение с целыми коэффициентами P(x1,x2,…,xn)=0 (Например, ax12+bx22+cx33=0). 10-ая проблема Гильберта Требуется выяснить, существует
- 5. В 1970 г. математик Ю.В.Матиясевич (СССР) доказал невозможность построения алгоритма решения этой задачи.
- 6. По описанию произвольного алгоритма и его исходных данных требуется определить остановится ли алгоритм на этих данных
- 7. любой теоремы из любой системы аксиом, которую пытался решить Лейбниц в XVII в., пытаясь построить алгоритм
- 8. основаны на методе сведения к этим задачам известных алгоритмически неразрешимых задач. Методы доказательства алгоритмической неразрешимости Задачи,
- 9. – функция, вычисляемая некоторым алгоритмом. Вычислимая функция (алгоритмически вычислимая) Теория вычислимости – раздел теории алгоритмов.
- 10. Пример невычислимой функции Анализ первых 800 знаков разложения π показывает, что f(n)=1 для n=0, 1, 2,
- 11. В теории алгоритмов было сформулировано понятие вычислительной машины и доказано, что для преобразования информации не обязательно
- 13. Скачать презентацию










 Презентация на тему Функция у=к/х, её свойства и график
Презентация на тему Функция у=к/х, её свойства и график  Производная функции
Производная функции Математическая статистика
Математическая статистика Это полезно знать
Это полезно знать Преобразование сумм тригонометрических функций в произведения. Преобразование простейших тригонометрических выражений
Преобразование сумм тригонометрических функций в произведения. Преобразование простейших тригонометрических выражений Математический маятник. Измерения
Математический маятник. Измерения Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Процедуры и функции работы со строками
Процедуры и функции работы со строками Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс
Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Деление суммы на число
Деление суммы на число Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Занятие математического кружка по теме Площадь. 5 класс
Занятие математического кружка по теме Площадь. 5 класс Понятие о задачах математической статистики
Понятие о задачах математической статистики Второй признак равенства треугольников. 7 класс
Второй признак равенства треугольников. 7 класс Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Решение задач на движение
Решение задач на движение Решение задач на применение свойств прямоугольных треугольников
Решение задач на применение свойств прямоугольных треугольников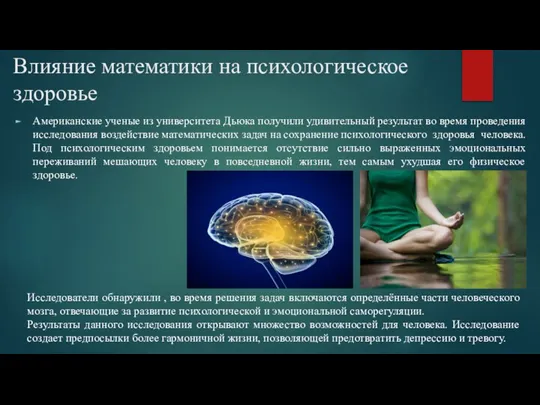 Влияние математики на психологическое здоровье
Влияние математики на психологическое здоровье Решаем задачи
Решаем задачи Логарифмы вокруг нас
Логарифмы вокруг нас Производная
Производная Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой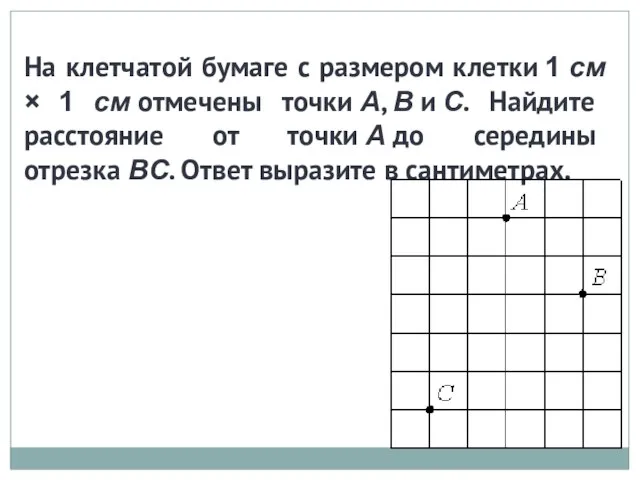 Решение задач
Решение задач ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата
Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата