Содержание
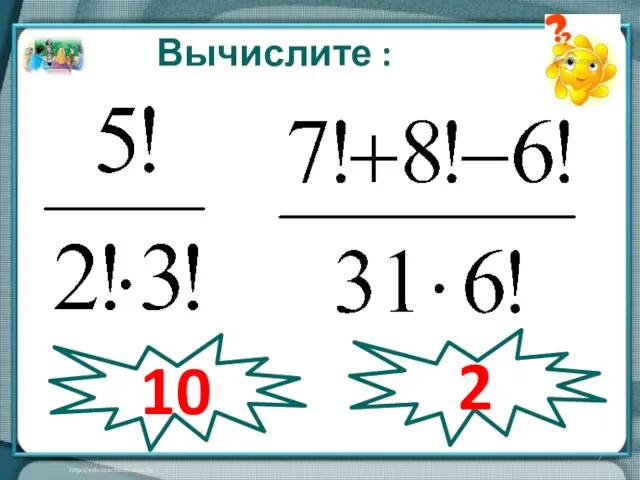
- 2. Вычислите : 10 2
- 3. Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда
- 4. Решение задачи: А А А В Б Б Б В Может быть такая последовательность: А может
- 5. Теорема о перестановках элементов конечного множества: n различных элементов можно расставить по одному на n различных
- 6. Вычислите : 56 24
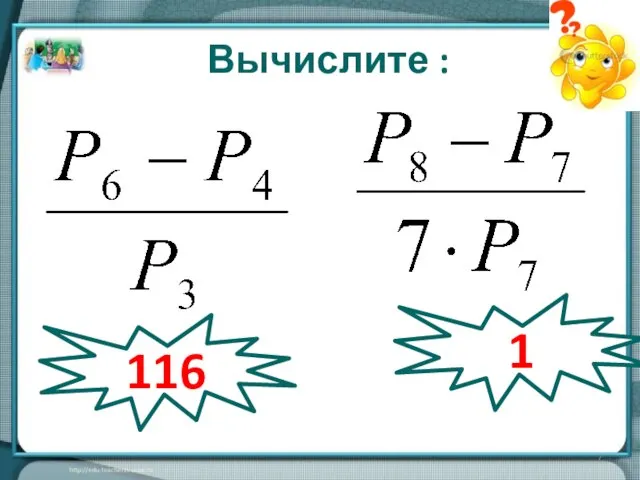
- 7. Вычислите : 116 1
- 8. 2Рх =12 Решите уравнение : 4
- 9. Задача: Пять друзей решили сфотографироваться. Сколькими способами их можно рассадить? 120 Сколько фигурок можно сложить из
- 10. Найдите количество всех способов, которыми можно составить трехцветный флаг из горизонтальных полос красного, белого и синего
- 11. Задача: Сколько трёхзначных чисел можно получить, используя числа 1,2,3? Это числа: 123, 132, 213, 231, 312,
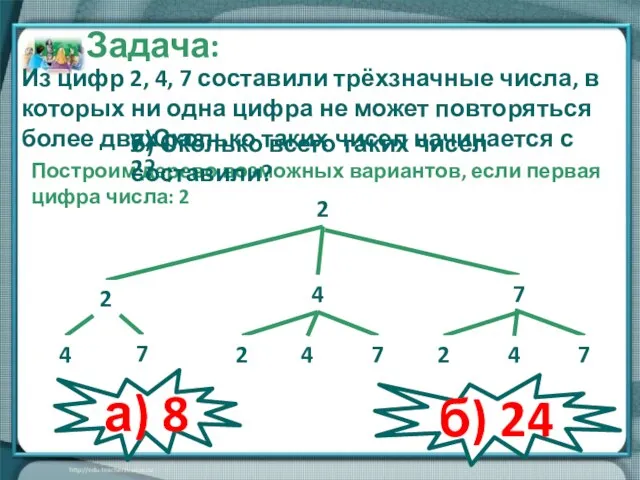
- 12. 2 4 2 7 4 7 2 7 2 7 4 4 Построим дерево возможных вариантов,
- 13. 247 274 224 227 242 272 244 Задача: Из цифр 2, 4, 7 составили трёхзначные числа.
- 14. Расставляем предметы по порядку Математика 6 Литература 5 Русский язык 4 Английский язык 3 Биология 2
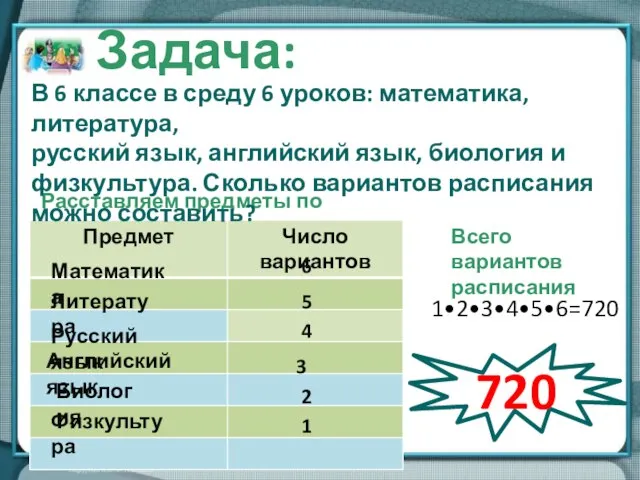
- 15. В 6 классе во вторник 5 уроков: физкультура, русский язык, литература, обществознание и математика. Сколько можно
- 16. Имеется девять различных книг, четыре из которых - учебники. Сколькими способами можно расставить эти книги на
- 17. Проказница мартышка, Осел, Козел, Да косолапый мишка затеяли сыграть квартет…Вам знакомо это произведение? Задача: 4!=24
- 18. Р5 = 5! Задача: Петя, Вася, Галя, Света и Марина садятся на скамейку. Сколькими способами можно
- 19. Задача: Сколькими способами Петя, Вася, Галя, Света и Марина могут сесть так, чтобы Галя и Марина
- 20. Задача: Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя был в
- 21. Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя и Вася не
- 22. Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Света не была второй
- 23. Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не сидела с
- 24. Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не была непосредственно
- 25. Сколькими способами можно переставить буквы в слове «эскиз»? Задача: 5!=120
- 26. Задача: Сколько слов можно получить, переставляя буквы в слове «переправа»? Чем отличается эта задача от предыдущей?
- 27. Сколько слов можно получить, переставляя буквы в словах: «молоко»? «математика»? Задача для самостоятельного решения: 120 1680
- 28. 1. Весной мама покупает ребенку много фруктов. Она купила банан, яблоко, апельсин, лимон, грушу и киви.
- 30. Скачать презентацию























 Сложение векторов
Сложение векторов Цилиндр
Цилиндр Игра-тренажёр Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр Уроки с Мальвиной. Табличное умножение и деление Параллелограмм и трапеция
Параллелограмм и трапеция Параллельные прямые. Свойства и признаки параллельных прямых
Параллельные прямые. Свойства и признаки параллельных прямых Распределенные системы. Математическое представление распределенной системы
Распределенные системы. Математическое представление распределенной системы Своя игра. Показательная и степенная функции. 10 класс
Своя игра. Показательная и степенная функции. 10 класс Развитие понятия о числе
Развитие понятия о числе Естественный отбор и его математические характеристики
Естественный отбор и его математические характеристики Сочетания. В чем отличие от размещений?
Сочетания. В чем отличие от размещений? Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Основные элементы комбинаторики и бином Ньютона. Тема 11.1
Основные элементы комбинаторики и бином Ньютона. Тема 11.1 Функция у-сосх, её свойства и график
Функция у-сосх, её свойства и график Конусы в нашей жизни
Конусы в нашей жизни Галерея великих имён
Галерея великих имён Функции и их графики
Функции и их графики Новогодняя сказка в Стране математики. Для детей 5-ти лет
Новогодняя сказка в Стране математики. Для детей 5-ти лет Разложение полиномов (многочленов) на сомножители. Лекция 2-03
Разложение полиномов (многочленов) на сомножители. Лекция 2-03 Определение функций. Построение и чтение графиков функций
Определение функций. Построение и чтение графиков функций Подготовка к ЕГЭ 2020
Подготовка к ЕГЭ 2020 Общая задача нелинейного программирования
Общая задача нелинейного программирования Решение графических задач на газовые законы
Решение графических задач на газовые законы Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Решение систем уравнений второй степени различными способами
Решение систем уравнений второй степени различными способами Построения проекций вершин ребер и граней предмета
Построения проекций вершин ребер и граней предмета Проценты. Определение, обозначение, вычисление, применение
Проценты. Определение, обозначение, вычисление, применение Объемы тел вращения
Объемы тел вращения