Содержание
- 2. ЗАДАНИЕ № 19 - 1 Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили
- 3. ЗАДАНИЕ № 19 - 2 Найдите четырёхзначное число, кратное 18, произведение цифр которого равно 24. В
- 4. ЗАДАНИЕ № 19 - 3 Найдите трехзначное натуральное число, большее 500, которое при делении на 4,
- 5. ЗАДАНИЕ № 19 - 4 Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна
- 6. ЗАДАНИЕ № 19 - 5 Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось
- 7. ЗАДАНИЕ № 19 - 6 Приведите пример трёхзначного натурального числа, большего 500, которое при делении на
- 8. ЗАДАНИЕ № 19 - 7 Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что
- 9. ЗАДАНИЕ № 19- 8 Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна их
- 10. ЗАДАНИЕ № 19 - 9 Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 5
- 11. ЗАДАНИЕ № 19 - 10 Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма
- 12. ЗАДАНИЕ № 19 - 11 Найдите трехзначное натуральное число, большее 600, которое при делении на 4,
- 13. ЗАДАНИЕ № 19 - 12 Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число
- 14. РЕШЕНИЕ № 19 -1 Число делится на 5, значит, его последняя цифра или 0, или 5.
- 15. РЕШЕНИЕ № 19 - 2 Если число кратно 18, оно кратно 2, 9, 3, 6: то
- 16. РЕШЕНИЕ № 19 - 3 При делении на 4 число даёт в остатке 2, следовательно, оно
- 17. РЕШЕНИЕ № 19 - 4 Пусть число имеет вид . Тогда условие записывается так: Можно заметить,
- 18. РЕШЕНИЕ № 19 - 5 Если число делится на 18, то оно также делится на 9
- 19. РЕШЕНИЕ № 19 - 6 По модулю 5 и 8 число имеет одинаковые остатки. Оно будет
- 20. РЕШЕНИЕ № 19 - 7 Разложим число 25 на слагаемые: 25 = 9 + 9 +
- 21. РЕШЕНИЕ № 19 - 8 Можно заметить, что если среди цифр есть хотя бы две единицы,
- 22. РЕШЕНИЕ № 19 - 9 Если число делится на 5 и на 9, то это число
- 23. РЕШЕНИЕ № 19 - 10 Разложим число 20 на слагаемые различными способами: 20 = 9 +
- 24. РЕШЕНИЕ № 19 - 11 При делении на 4 число даёт в остатке 3, следовательно, оно
- 25. РЕШЕНИЕ № 19 - 12 Если число делится на 27, тогда оно делится на 3 и
- 27. Скачать презентацию
























 Задачи
Задачи 20140617_svoystva_funktsiy_9_klass
20140617_svoystva_funktsiy_9_klass Почти все об углах
Почти все об углах Презентация на тему Справочное пособие по геометрии
Презентация на тему Справочное пособие по геометрии  Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Вычисление площадей
Вычисление площадей Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Решение систем неравенств. 8 класс
Решение систем неравенств. 8 класс Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг Путешествие в страну дроби
Путешествие в страну дроби Решите неравенства
Решите неравенства Графики уравнений, содержащих модули
Графики уравнений, содержащих модули Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел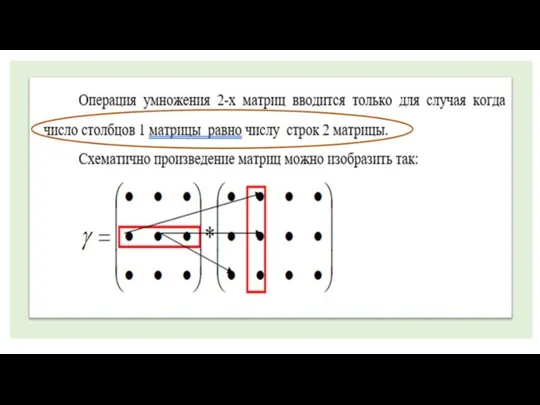 Операция умнодения 2 матриц
Операция умнодения 2 матриц Метод резолюций в алгебре высказываний
Метод резолюций в алгебре высказываний Все действия с дробями
Все действия с дробями Цифра ноль
Цифра ноль Осевая симметрия
Осевая симметрия Мода и медиана
Мода и медиана Этот вездесущий треугольник
Этот вездесущий треугольник Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції Тела вращения
Тела вращения Возведение комплексных чисел в степень
Возведение комплексных чисел в степень Векторы в пространстве. Решение задач по готовым чертежам
Векторы в пространстве. Решение задач по готовым чертежам Пифагор Самосский. Теорема Пифагора
Пифагор Самосский. Теорема Пифагора Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября)
Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября) Площадь круга. Геометрическая сказка. 6 класс
Площадь круга. Геометрическая сказка. 6 класс