Содержание
- 2. «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле» А.Н. Крылов
- 3. Устно: 1. Определение числовой функции. 2. Область определения числовой функции. 3. Область значения числовой функции. 4.
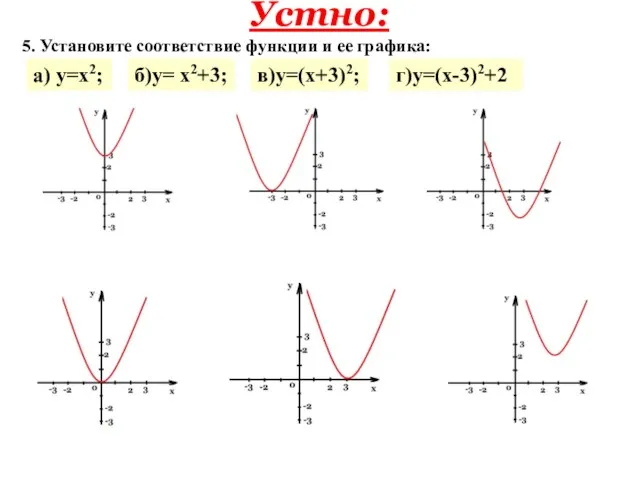
- 4. Устно: 5. Установите соответствие функции и ее графика: а) у=х2; б)у= х2+3; г)у=(х-3)2+2 в)у=(х+3)2;
- 5. Промежутки, симметричны относительно начала координат, значит для любого х из этого промежутка (-х) также принадлежит этому
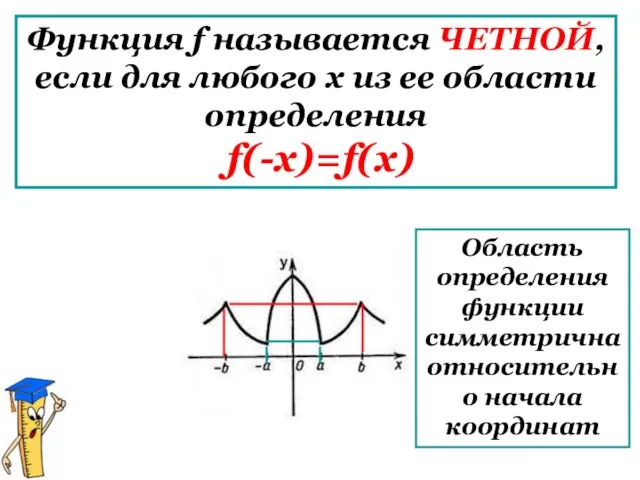
- 6. Функция f называется ЧЕТНОЙ, если для любого х из ее области определения f(-x)=f(x) Область определения функции
- 7. Функция f называется НЕЧЕТНОЙ, если для любого х из ее области определения f(-x)=-f(x) a - a
- 8. Нечетные функции Четная функция Четность и нечетность тригонометрических функций
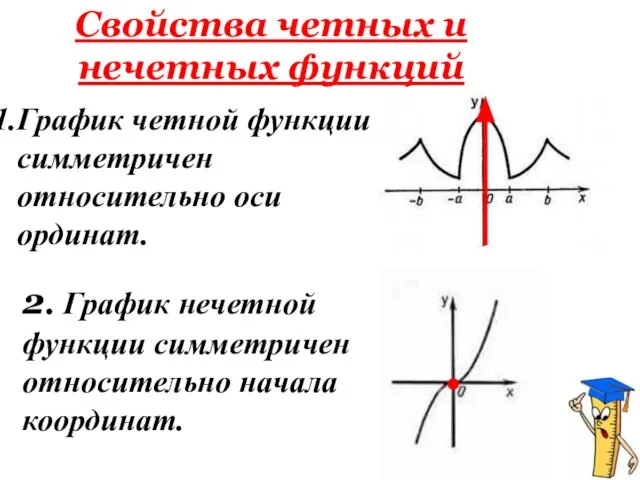
- 9. График четной функции симметричен относительно оси ординат. 2. График нечетной функции симметричен относительно начала координат. Свойства
- 10. 1. Доказать, что функция f(x )четная
- 11. 2. Доказать, что функция g(x ) нечетная
- 12. 3. Является ли функция f(x ) четной или нечетной?
- 13. 3. Докажите, что функции являются четными
- 14. 3. Докажите, что функции являются нечетными
- 15. Вариант 1. 1. Докажите, что функция f(x)=4х3 +7х является нечетной. 2. Приведите пример четной функции. Самостоятельная
- 16. п. 4 (1), № 58(а), №60 (б), №69(б) Домашнее задание:
- 17. Оцените свою работу на уроке. Удовлетворены ли вы результатом своей работы?
- 18. Спасибо за урок! Всем удачи!
- 20. Скачать презентацию














 Понятие функции
Понятие функции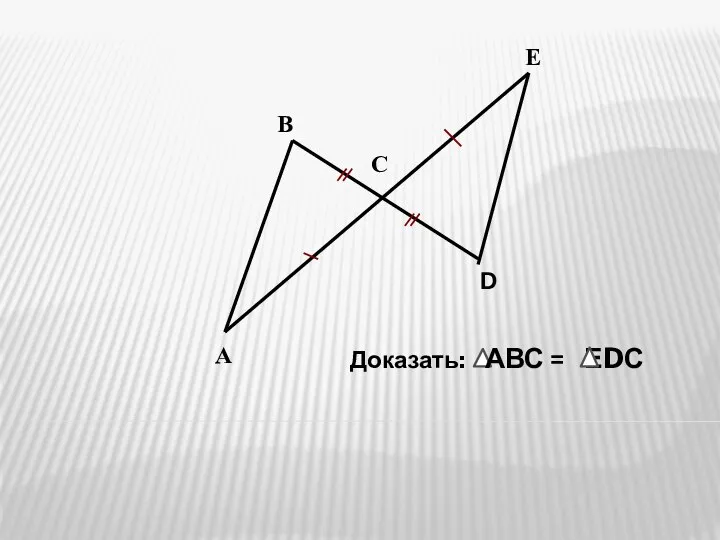 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач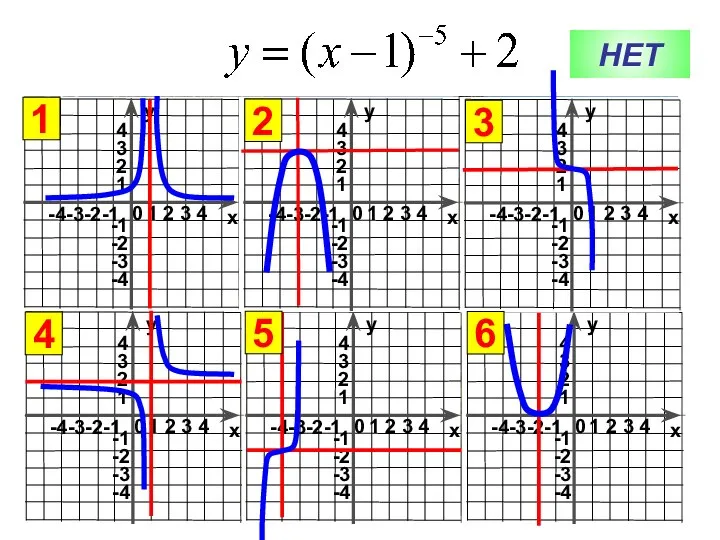 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого