Декартовы координаты на плоскости (решение задач)

Суть метода координат заключается в том, что введение системы координат позволяет записать условие задачи в координатах и решать её, используя знания по алгебре.

ОСНОВНЫЕ ФОРМУЛЫ МЕТОДА КООРДИНАТ
1. РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ С ЗАДАННЫМИ КООРДИНАТАМИ

x
y
O
A (x1; y1)
B (x2; y2)
C (x0; y0)
x1
x2
y1
y2
x0
y0
2. ФОРМУЛЫ КООРДИНАТ СЕРЕДИНЫ ОТРЕЗКА
середина отрезка АВ:

1.Найти АВ и
координаты
середины АВ- т.М
3.Четырёхугольник АВСD
задан координатами вершин
А(-2;3), В(0;6), С(5;7),D(3;4).
Доказать,
что этот четырёхугольник-
ПАРАЛЛЕЛОГРАММ.
(Какой признак параллело -
грамма мы можем проверить?)
2.Найти расстояние
от точки А (-5;12) до
начала координат
РЕШИТЬ ЗАДАЧИ:

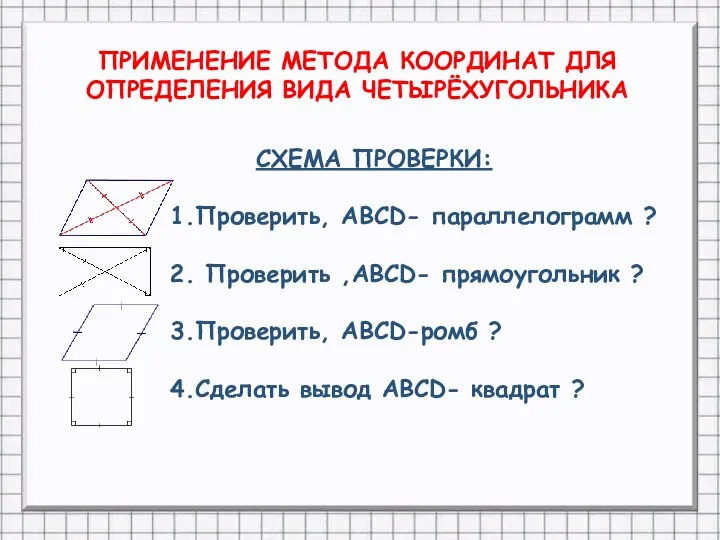
ПРИМЕНЕНИЕ МЕТОДА КООРДИНАТ ДЛЯ ОПРЕДЕЛЕНИЯ ВИДА ЧЕТЫРЁХУГОЛЬНИКА
СХЕМА ПРОВЕРКИ:
1.Проверить, АВСD- параллелограмм ? 2. Проверить ,АВСD- прямоугольник ?
3.Проверить, АВСD-ромб ?
4.Сделать вывод АВСD- квадрат ?

ДЛЯ ПРОВЕРКИ ИСПОЛЬЗОВАТЬ ПРИЗНАКИ:
т.О-середина
АС и ВD
параллелограмм
вывод
АВСD
квадрат
АВ = ВС
ромб
АС = ВD
прямоугольник
D
С
В
А
D
А
В
С
В
А
С
D

РЕШИТЬ ЗАДАЧИ:
1.Доказать,что четырёхугольник
АВСD с вершинами
А(2;6), В(5;1), С(2;-4),D(-1;1)-
РОМБ
2.Доказать,что четырёхугольник
АВСD с вершинами
А(-2;2), В(4;2),С(4;-1),D(-2;-1)-
ПРЯМОУГОЛЬНИК
3.Определить вид четырёхугольника
АВСD с вершинами
А(0;8), В(-6;0),С(2;-6),D(8;2)

1.Найти периметр
ΔАВС, если А(-1;2),
В( 3;-1), С(-1;-1)
РЕШИТЬ ЗАДАЧИ:
3.Какая из точек Q(2;4)
или F(-3;2) лежит
ближе к началу координат?
2. Даны точки А(-2;5) и В(1;8).
Найти точку, равноудалённую
от точек А и В, которая лежит:
1) на оси Ох;
2) на оси Оу;
3) на отрезке АВ
4. АВСD-параллелограмм.
А(-2;-2), С(4;1), D(-1;1).
Найти координаты вершины B.
По учебнику:
№ 940(а,б),947(а),
951(а)
Учебник. Л.С.Атанасян. Геометрия 7-9 классы. М.: Просвещение,2016

ИТОГ УРОКА
1.Как с помощью изученных формул доказать, что ∆:
- равнобедренный ? - равносторонний ?
- прямоугольный ?
2. Как проверить, лежат ли на одном отрезке
3 точки, если заданы их координаты?
3. Как найти конец отрезка по известным
координатам середины и другого конца отрезка?
4. Какие признаки параллелограмма ,ромба,
прямоугольника , надо использовать для
определения вида 4-х угольника с помощью МК?
5. Как доказать, что фигура-квадрат ?