Золотое сечение и симметрия

Что связывает золотое сечение со снежинкой?
Подсолнух и золотая спираль. Что общего?
С каким определением в геометрии связана красота человеческого лица?

1. Снежинки являются кристаллами, а все кристаллы симметричны. Это значит, что в каждом кристаллическом многограннике можно найти плоскости симметрии, оси симметрии, центры симметрии и другие элементы симметрии так, чтобы совместились друг с другом одинаковые части многогранника.

2. В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения. Семена подсолнуха располагаются двумя рядами по закрученным спиралям в разные стороны.

3. Чем красивее кажется лицо, тем ближе его пропорции к идеальным, а они в свою очередь определяются золотой пропорцией и симметрией.

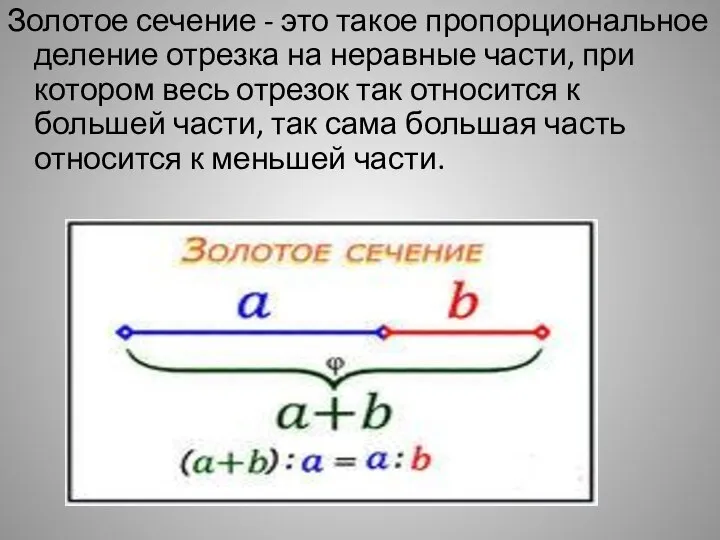
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, так сама большая часть относится к меньшей части.

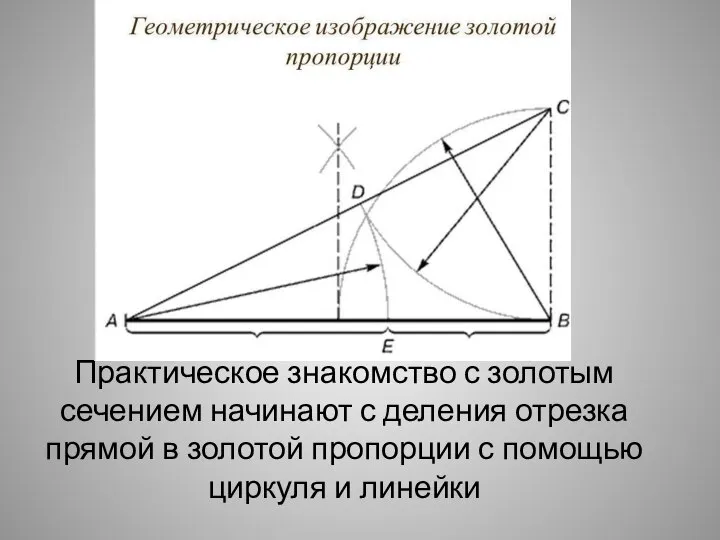
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки

ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ

Золотая симметрия в дизайне

Виды симметрии
Зеркальная;
Осевая;
Зеркально-осевая;
Винтовая.

Задача
Найти площадь треугольника со сторонами 10 см, 19 см и 8 см.

Ответ
Проверив условие при помощи неравенства треугольника, учащиеся убеждаются, что условие задачи противоречиво (8 < 19 – 10, т.е. одна из сторон треугольника меньше разности двух других сторон, а не больше!), откуда и следует вывод, что задача не имеет решения.

Междисциплинарные связи с другими науками
Физика
Химия
История
Биология