Содержание
- 2. С.И.Ожегов, Н.Ю.Шведова «Вероятность – возможность исполнения, осуществимости чего-нибудь». А.Н.Колмогоров «Вероятность математическая – это числовая характеристика степени
- 3. Математическая модель «игральная кость» Выпадение каждой грани при многократном бросании кубика имеет одинаковую вероятность Испытание –
- 4. УСТНАЯ РАБОТА 1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало 4 очка?
- 5. 1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна
- 6. Решите задачу Люда дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность
- 7. Решите задачу 7. Наташа и Вика играют в кости. Они бросают игральную кость по одному разу.
- 8. Решите задачу 9. Коля и Лёша играют в кости. Они бросают игральную кость по одному разу.
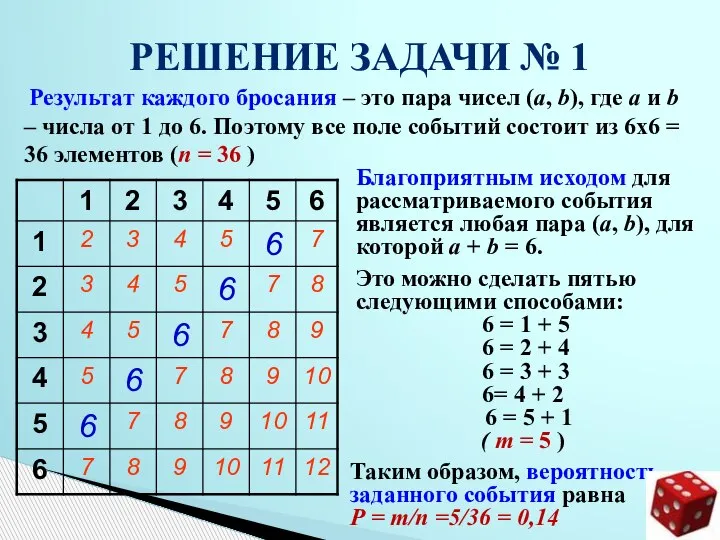
- 9. Результат каждого бросания – это пара чисел (a, b), где a и b – числа от
- 10. Результат каждого бросания – 36 равновозможных исходов РЕШЕНИЕ ЗАДАЧИ № 2 Благоприятных исходов – 2 Вероятность
- 11. Результат каждого бросания – 36 равновозможных исходов РЕШЕНИЕ ЗАДАЧИ № 3 Благоприятных исходов – 3 Вероятность
- 12. РЕШЕНИЕ ЗАДАЧИ № 4 Первое бросание Второе бросание Сумма очков 3 + 6 = 9 4
- 13. РЕШЕНИЕ ЗАДАЧИ № 5 Первое бросание Второе бросание Сумма очков 1 + 5 = 6 2
- 14. РЕШЕНИЕ ЗАДАЧИ № 6 Первое бросание Второе бросание Сумма очков 1 + 4 = 5 2
- 15. РЕШЕНИЕ ЗАДАЧИ № 7 Наташа Вика Сумма очков 2 + 6 = 8 3 + 5
- 16. РЕШЕНИЕ ЗАДАЧИ № 8 Тоня Нина Сумма очков 1 + 5 = 6 2 + 4
- 17. РЕШЕНИЕ ЗАДАЧИ № 9 У Коли выпало 3 очка. У Лёши равновозможных исходов – 6 Благоприятствующих
- 18. РЕШЕНИЕ ЗАДАЧИ № 10 У Миши равновозможных исходов – 6 · 6 · 6 = 216
- 19. РЕШЕНИЕ ЗАДАЧИ № 11 Первая Вторая Третья Сумма очков 4 + 6 + 6 = 16
- 21. Скачать презентацию

















 Функция регрессии
Функция регрессии Умножение 8 и на 8, соответствующие случаи деления
Умножение 8 и на 8, соответствующие случаи деления Арифметические действия
Арифметические действия Пять великих математиков
Пять великих математиков Расширение и углубление знаний учащихся о преобразованиях графиков функций
Расширение и углубление знаний учащихся о преобразованиях графиков функций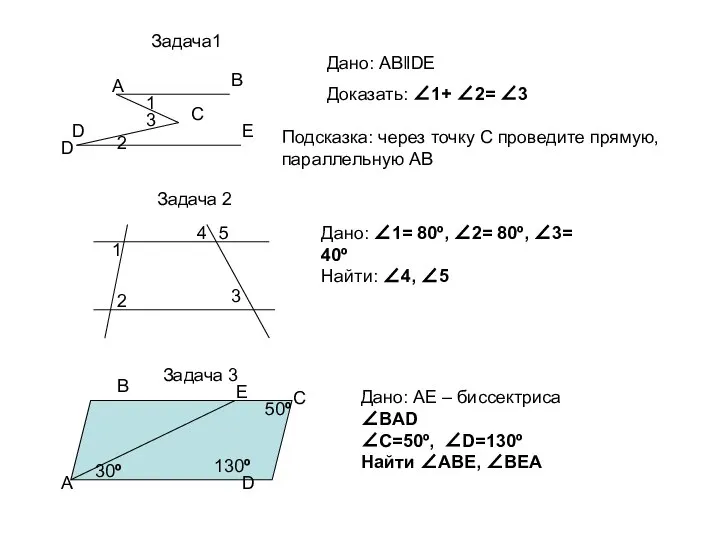 Параллельные прямые (тест)
Параллельные прямые (тест) Подготовка к ГИА. Модуль Геометрия
Подготовка к ГИА. Модуль Геометрия Окружность. (Задача 18. Вариант 105)
Окружность. (Задача 18. Вариант 105) Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата
Выбор математической модели воздушного винта для оценки его влияния на аэродинамические характеристики летательного аппарата Старинные меры массы и длины
Старинные меры массы и длины Обзор приложений копул к задачам Байесовской классификации при машинном обучении
Обзор приложений копул к задачам Байесовской классификации при машинном обучении Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Հետաքրքրաշարժ մաթեմատիկա 4 dasaran
Հետաքրքրաշարժ մաթեմատիկա 4 dasaran Тема 1
Тема 1 Треугольник. Высота в треугольнике
Треугольник. Высота в треугольнике Обратная матрица. Матричные уравнения. Лекция 4
Обратная матрица. Матричные уравнения. Лекция 4 Построение сечений параллелепипеда (задачи)
Построение сечений параллелепипеда (задачи)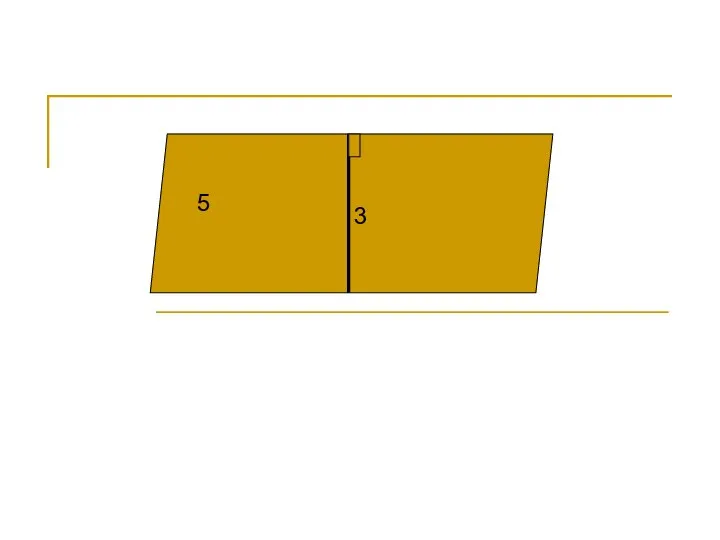 Площадь трапеции. Чертежи для решения задач
Площадь трапеции. Чертежи для решения задач Теория вероятностей. ТВиС
Теория вероятностей. ТВиС Комбинаторика. 11 класс
Комбинаторика. 11 класс Геометрические построения
Геометрические построения Дробно-линейная функция и ее график
Дробно-линейная функция и ее график Признаки равенства треугольников
Признаки равенства треугольников Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Логические задачи. Математика и информатика. Тетрадь для 1–2 классов
Логические задачи. Математика и информатика. Тетрадь для 1–2 классов Презентация на тему Вводный урок математики в 5 классе
Презентация на тему Вводный урок математики в 5 классе  Понятие объема. Объем
Понятие объема. Объем Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни