Слайд 2Гистограмма распределения.
Полигон распределения.
Кумулята.
Тренд.

Слайд 3Гистограмма распределения.
(Гистограмма - от греческого "гистос"- ткань; строение.) Это вид столбиковой

диаграммы, применяемой для интервального ряда. На оси ОХ (абсцисс) откладываются интервалы значений варьирующего признака, а на оси OY (ординат) частоты признака, соответствующего масштаба.
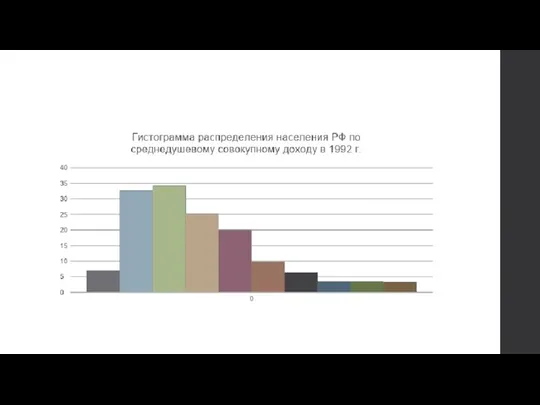
Слайд 4Пример 4.1.
Распределение населения РФ по среднедушевому совокупному доходу в 1992 г.

Слайд 6Плотность - величина равная отношению частоты признака к величине соответствующего интервала, обозначается

знаком "f".
f = Рi /hi
где f - плотность распределения;
Рi - частота признака;
hi- величина интервала.
Слайд 7Полигон распределения.
(Полигон - с греческого - многоугольник). Это вид линейного графика, представляющий

собой замкнутую ломаную линию (с обязательными точками нулевых частот до первой и после последней вариант признака).
Слайд 8Пример 4.2.
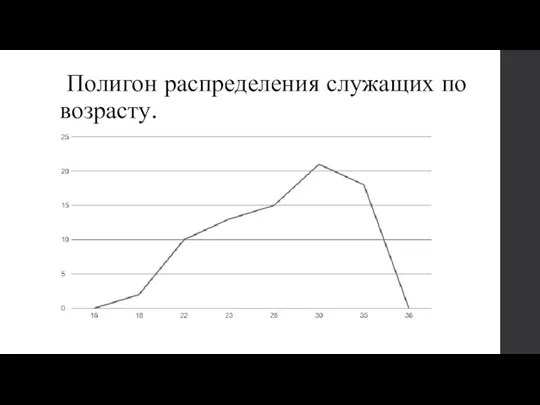
Распределение служащих по возрасту:

Слайд 9 Полигон распределения служащих по возрасту.
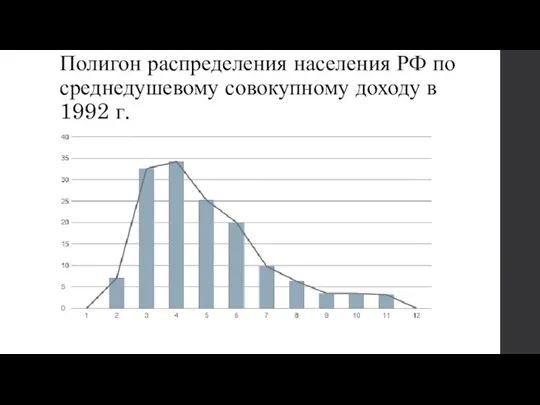
Слайд 10Полигон распределения населения РФ по среднедушевому совокупному доходу в 1992 г.
Слайд 11Полигон распределения полезно получить в случае неравных интервалов. Он точнее характеризует закономерность

изменения значений признака и решает проблему открытых интервалов. Кроме того, правильно построенный полигон распределения позволяет выявить тенденцию, скрытую табличной формой представления данных.
Слайд 12Структурная группировка грамотного сельского населения N-ского района по возрасту по данным 1928

года:
Слайд 13Полигон структурной группировки грамотного сельского населения N-ского района по возрасту по данным
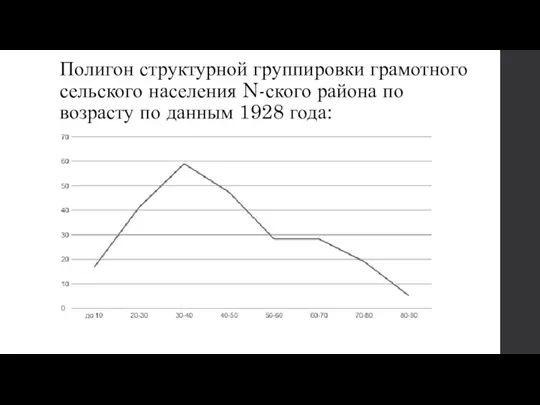
1928 года:
Слайд 14Кумулята
Кумулята (от позднелатинского "скопление"). Это вид линейного графика, представляющий собой плавную кривую.

На оси абсцисс откладывают значения рассматриваемого признака, а на оси ординат - накопленные частоты. Чтобы получить такой график необходимо предварительно преобразовать вариационный ряд в ряд накопленных частот (кумулятивный ряд). Он получается путем последовательного сложения частоты каждого класса с суммой предыдущих классов.
Слайд 15Пример 4.4. Распределение населения РФ по среднедушевому совокупному доходу в 1992 г.

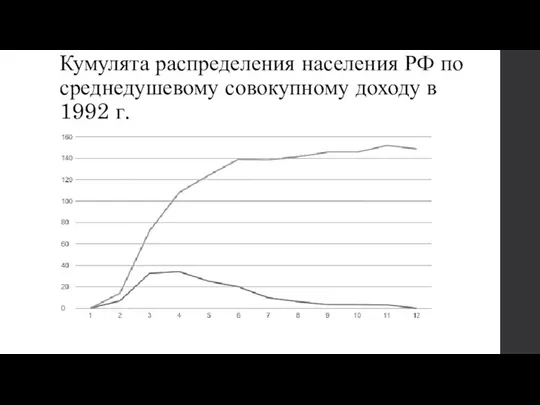
Слайд 16Кумулята распределения населения РФ по среднедушевому совокупному доходу в 1992 г.
Слайд 17Тренд.
Обнаружить тренд можно различными методами - методом скользящей средней, наименьших квадратов, с

помощью среднего прироста и т.д. Одним из приемов определения тренда выступает график. Для этого в системе координат уровни динамического ряда отмечают точками, а затем на основе зрительного анализа месторасположения точек проводят среднюю линию, которая называется трендом и отражает основную тенденцию развития.
Слайд 18Пример 4.5. Динамика урожайности картофеля в 1883-1892 гг.

Слайд 19Динамика урожайности картофеля в 1883-1892 гг.
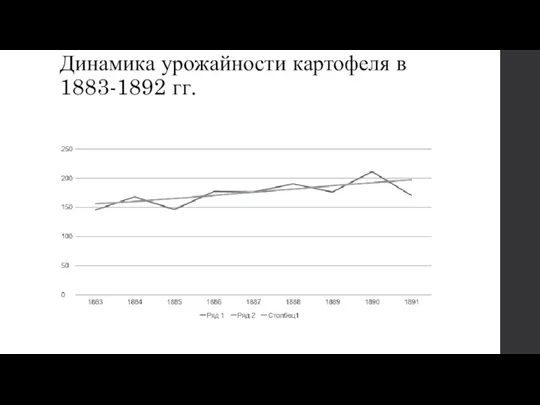
Слайд 20Задачи графического метода не исчерпываются наглядностью. Графики позволяют приближенно получить средние характеристики

- моду и медиану. Графиками проверяется характер и форма зависимости между признаками, что особенно важно для доказательства правомерности применения методов корреляционного анализа. На графике сразу видны пределы изменения показателей, их колеблемость, скорость изменения, выявляются и характеризуются закономерности.
Слайд 21В зависимости от задач исследования графики размещают в тексте работы или в

приложении к ней. Чаще всего небольшие по формату рисунки иллюстративного характера, подтверждающие ранее полученные выводы, располагают по мере изложения материала в тексте исследования.
Слайд 22Вместе с тем, графический метод имеет свои ограничения.
Во- первых, график не

может включить столько данных, сколько может войти в таблицу.
Во-вторых, на графике показываются всегда приблизительные, округленные значения, а значит пропадают детали, фиксируется только общая ситуация.
В-третьих, построение графика, его точность во многом зависят от аккуратности исследователя.




















 Презентация на тему Площадь треугольника
Презентация на тему Площадь треугольника  Координаты вектора
Координаты вектора Примеры на сложение
Примеры на сложение Число 10
Число 10 Вероятность события (часть 3)
Вероятность события (часть 3) Готовимся к ЕГЭ
Готовимся к ЕГЭ Теория вероятностей
Теория вероятностей Свойства степеней
Свойства степеней Повторение 1 класс
Повторение 1 класс Кенгуру – математика для всех
Кенгуру – математика для всех Таблица умножения на 2
Таблица умножения на 2 Косинус угла
Косинус угла Презентация по математике "Решение задач. Закрепление" -
Презентация по математике "Решение задач. Закрепление" -  Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Системы булевых функций. Лекция 5
Системы булевых функций. Лекция 5 Простейшие линейные цепи при гармоническом воздействии
Простейшие линейные цепи при гармоническом воздействии Математический калейдоскоп. Игра
Математический калейдоскоп. Игра Проценты
Проценты Дифференциальные уравнения
Дифференциальные уравнения Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Геометрия. Заготовка
Геометрия. Заготовка Презентация на тему Скорость, время, расстояние
Презентация на тему Скорость, время, расстояние  Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Интеграл. Определенный интеграл. Свойства
Интеграл. Определенный интеграл. Свойства Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Математическая индукция
Математическая индукция Математический кроссворд. Для учащихся 5-6 классов
Математический кроссворд. Для учащихся 5-6 классов Бинарные отношения
Бинарные отношения