Фракталы

ЧТО ТАКОЕ ФРАКТАЛ
И КАК ОН ВЫГЛЯДИТ
Фракта́л (лат. Fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.

ФРАКТАЛЫ В ПРИРОДЕ
Что общего у дерева, берега моря, облака или кровеносных сосудов у нас в руке? Существует одно свойство структуры, присущее всем перечисленным предметам: они самоподобны. От ветки, как и от ствола дерева, отходят отростки поменьше, от них — еще меньшие, и т. Д., то есть ветка подобна всему дереву. Похожим образом устроена и кровеносная система: от артерий отходят артериолы, а от них — мельчайшие капилляры, по которым кислород поступает в органы и ткани. Посмотрим на космические снимки морского побережья: мы увидим заливы и полуострова; взглянем на него же, но с высоты птичьего полета: нам будут видны бухты и мысы; теперь представим себе, что мы стоим на пляже и смотрим себе под ноги: всегда найдутся камешки, которые дальше выдаются в воду, чем остальные. То есть береговая линия при увеличении масштаба остается похожей на саму себя. Это свойство объектов американский (правда, выросший во Франции) математик Бенуа Мандельброт назвал фрактальностью, а сами такие объекты — фракталами (от латинского fractus — изломанный).
С береговой линией, а точнее, с попыткой измерить ее длину, связана одна интересная история, которая легла в основу научной статьи Мандельброта, а также описана в его книге «Фрактальная геометрия природы». Речь идет об эксперименте, который поставил Льюис Ричардсон (Lewis Fry Richardson) — весьма талантливый и эксцентричный математик, физик и метеоролог. Одним из направлений его исследований была попытка найти математическое описание причин и вероятности возникновения вооруженного конфликта между двумя странами. В числе параметров, которые он учитывал, была протяженность общей границы двух враждующих стран. Когда он собирал данные для численных экспериментов, то обнаружил, что в разных источниках данные об общей границе Испании и Португалии сильно отличаются. Это натолкнуло его на следующее открытие: длина границ страны зависит от линейки, которой мы их измеряем. Чем меньше масштаб, тем длиннее получается граница. Это происходит из-за того, что при большем увеличении становится возможным учитывать всё новые и новые изгибы берега, которые раньше игнорировались из-за грубости измерений. И если при каждом увеличении масштаба будут открываться ранее не учтенные изгибы линий, то получится, что длина границ бесконечна! Правда, на самом деле этого не происходит — у точности наших измерений есть конечный предел. Этот парадокс называется эффектом Ричардсона (Richardson effect).
В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности. Помимо фрактальной живописи фракталы используются в теории информации для сжатия графических данных (здесь в основном применяется свойство самоподобия фракталов — ведь чтобы запомнить небольшой фрагмент рисунка и преобразования, с помощью которых можно получить остальные части, требуется гораздо меньше памяти, чем для хранения всего файла). Добавляя в формулы, задающие фрактал, случайные возмущения, можно получить стохастические фракталы, которые весьма правдоподобно передают некоторые реальные объекты — элементы рельефа, поверхность водоемов, некоторые растения, что с успехом применяется в физике, географии и компьютерной графике для достижения большего сходства моделируемых предметов с настоящими. В радиоэлектронике в последнее десятилетие начали выпускать антенны, имеющие фрактальную форму. Занимая мало места, они обеспечивают вполне качественный прием сигнала. А экономисты используют фракталы для описания кривых колебания курсов валют (это свойство было открыто Мандельбротом более 30 лет назад).

КАКИЕ БЫВАЮТ ФРАКТАЛЫ
Геометрические фракталы
Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную – генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ
Алгебраические фракталы
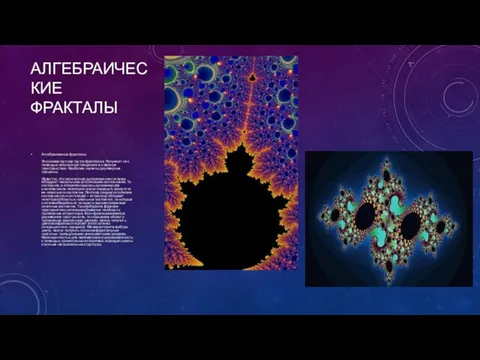
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят – аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.

СТОХАТИЧЕСКИЕ ФРАКТАЛЫ
Стохастические фракталы
Стохастические фракталы получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные – несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
ПРИМЕРЫ ФРАКТАЛОВ
множество Кантора — нигде не плотное несчетное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины.
Треугольник Серпинского и ковер Серпинского — аналоги множества Кантора на плоскости (треугольник Паскаля).