- Главная
- Математика
- Алгоритм Евклида

Содержание
Слайд 3Когда необходимо вычислить НОД нескольких чисел
можно применить несколько методов:
распространение алгоритма Евклида,
Когда необходимо вычислить НОД нескольких чисел
можно применить несколько методов:
распространение алгоритма Евклида,

базирующегося на следующих свойствах:
а) НОД (0,…,0,a,0,…,0)=a;
b) НОД (a1,…,ai,…,an)=
НОД (a1 mod ai ,…,ai,…,an mod ai) при ai≠0.
2) метод заключается в повторном применении алгоритма Евклида для двух целых чисел.
Он основан на следующем свойстве:
НОД (a1,…,an)=НОД(a1,НОД(a2,…,an)),
которое порождает рекурсивный алгоритм
вычисления НОД. Именно
НОД(a1,…,an)=НОД(НОД(a1,a2),a3,…,an),
что является основой соответствующего
итеративного алгоритма.
а) НОД (0,…,0,a,0,…,0)=a;
b) НОД (a1,…,ai,…,an)=
НОД (a1 mod ai ,…,ai,…,an mod ai) при ai≠0.
2) метод заключается в повторном применении алгоритма Евклида для двух целых чисел.
Он основан на следующем свойстве:
НОД (a1,…,an)=НОД(a1,НОД(a2,…,an)),
которое порождает рекурсивный алгоритм
вычисления НОД. Именно
НОД(a1,…,an)=НОД(НОД(a1,a2),a3,…,an),
что является основой соответствующего
итеративного алгоритма.
Слайд 4Теорема Дирихле. Если a и b два натуральных числа, выбранные случайно, то
Теорема Дирихле. Если a и b два натуральных числа, выбранные случайно, то

вероятность того, что они взаимно простые равна
Теорема Ламе. Число итераций, необходимых для
вычисления НОД(а,b), а>b>0, мажорируется
5-кратным числом десятичных знаков наименьшего из этих двух чисел. Более формально, если n является искомым числом итераций, то
или
Главный результат – сложность алгоритма Евклида
для целых чисел логарифмическая по отношению
к наименьшему из двух чисел. В оценке Ламе
коэффициент 5 оптимален, но мажорирующая
функция (O(log b)) таковой не является.
Теорема Ламе. Число итераций, необходимых для
вычисления НОД(а,b), а>b>0, мажорируется
5-кратным числом десятичных знаков наименьшего из этих двух чисел. Более формально, если n является искомым числом итераций, то
или
Главный результат – сложность алгоритма Евклида
для целых чисел логарифмическая по отношению
к наименьшему из двух чисел. В оценке Ламе
коэффициент 5 оптимален, но мажорирующая
функция (O(log b)) таковой не является.
Следующая -
Афония
 Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Массивы. Работа с массивами
Массивы. Работа с массивами Виды треугольников. 5 класс
Виды треугольников. 5 класс Сложение и вычитание многочленов
Сложение и вычитание многочленов Интегрирование на подмножествах (Кратный интеграл)
Интегрирование на подмножествах (Кратный интеграл)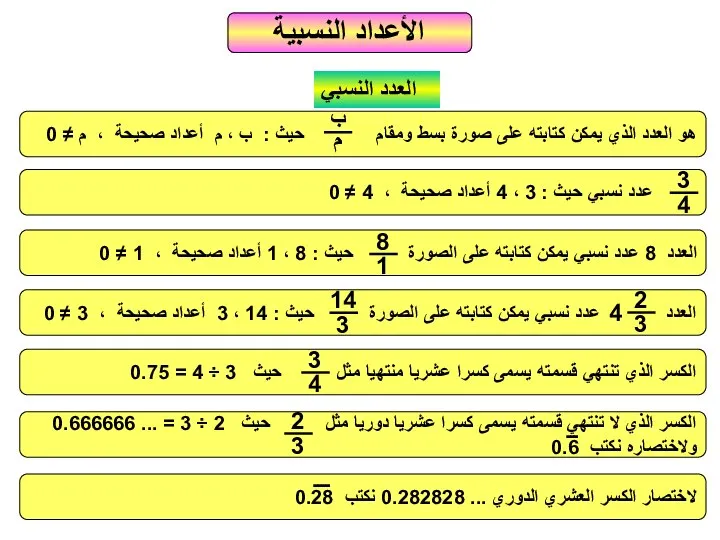 الأعداد انسبية
الأعداد انسبية Решение неравенств методом интервалов
Решение неравенств методом интервалов Интегрирование некоторых классов функций
Интегрирование некоторых классов функций Презентация на тему Среднее арифметическое (5 класс)
Презентация на тему Среднее арифметическое (5 класс)  Специальная теория относительности
Специальная теория относительности Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Геометрическая прогрессия
Геометрическая прогрессия Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Сокращение дробей
Сокращение дробей Алгоритмы в нашей жизни
Алгоритмы в нашей жизни Выражения с переменными
Выражения с переменными Л11 Производная функции
Л11 Производная функции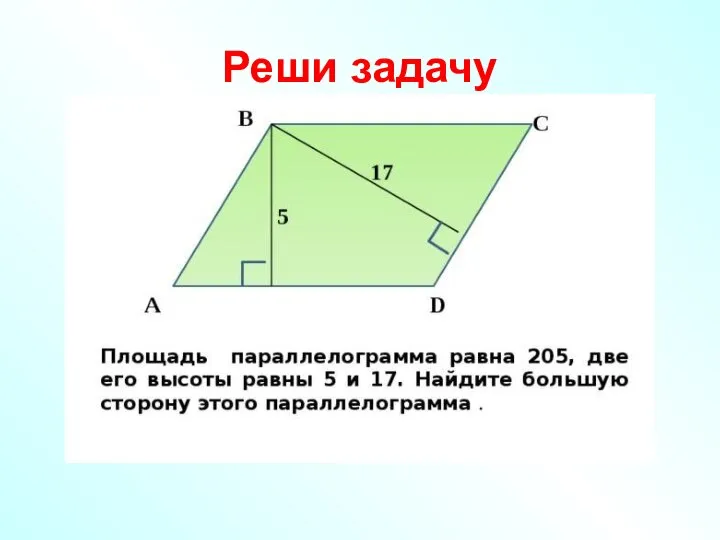 Решение задач на площадь параллелограмма
Решение задач на площадь параллелограмма Действительные числа и преобразования алгебраических выражений (домашнее задание)
Действительные числа и преобразования алгебраических выражений (домашнее задание) Графическое решение уравнений
Графическое решение уравнений Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Коэффициент корреляции
Коэффициент корреляции Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Решение задач
Решение задач Математический калейдоскоп
Математический калейдоскоп Музей геометрии
Музей геометрии Своя Игра! Математика
Своя Игра! Математика Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости