Исторические задачи по математике

«…Геометрия владеет двумя сокровищами: Одно из них- это золотое сечение, и другое- это........»
Иоганн Кеплер.

1. Существует ли число, квадрат которого равен 10?
2. По какой формуле находится площадь квадрата?
3. По какой формуле находится площадь прямоугольника?
4. Как называется треугольник, в котором один угол прямой?
5. Как называется сторона, лежащая напротив прямого угла?
6. Как называется меньшая сторона прямоугольного треугольника?

1. Нет
2. (S=a^2)
3. S=a*b
4. прямоугольный
5. гипотенуза
6. катет

Квадрат, построенный на гипотенузе прямоугольного треугольника равен сумме квадратов, построенных на катетах

Пифагор Самосский
(ок. 580 — ок. 500 до н. э.) древнегреческий философ, религиозный и политический деятель, математик, создатель религиозно-филосовской школы пифагорейцев.
В честь Пифагора назван кратер на Луне.

«…Геометрия владеет двумя сокровищами: Одно из них- это золотое сечение, и другое- это ТЕОРЕМА ПИФАГОРА.»
Иоганн Кеплер

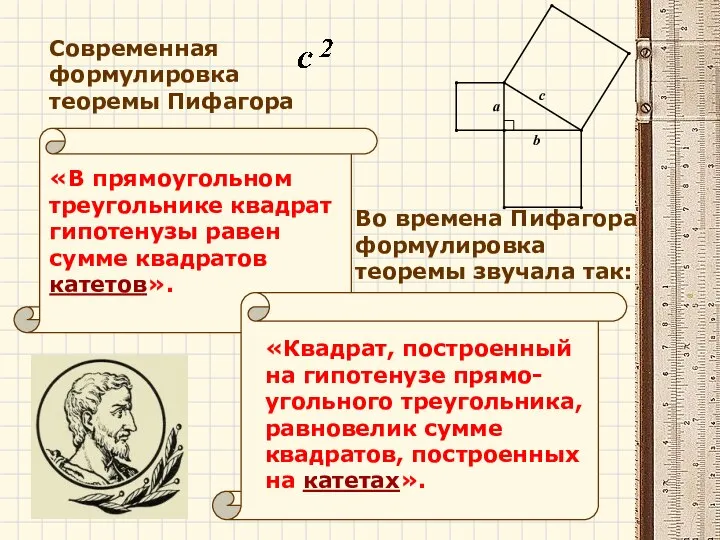
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме квадратов, построенных на катетах».
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Во времена Пифагора формулировка теоремы звучала так:
Современная формулировка
теоремы Пифагора
b
c
а

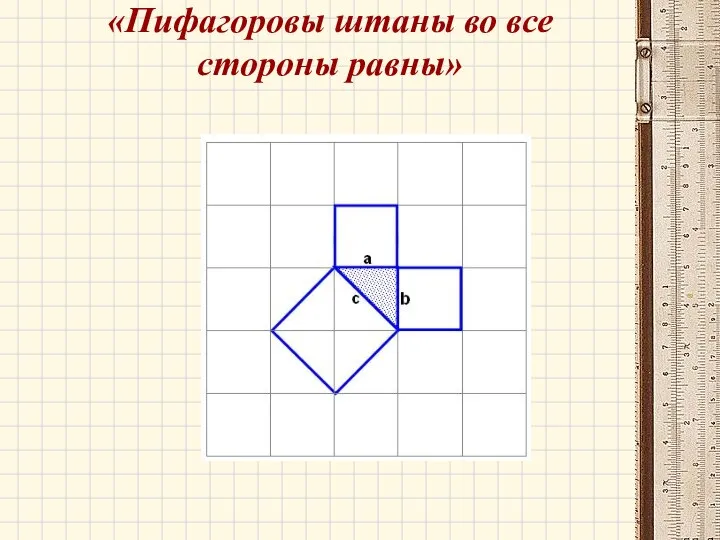
«Пифагоровы штаны во все стороны равны»

Задача индийского математика
XII века Бхаскары
ИСТОРИЧЕСКИЕ ЗАДАЧИ

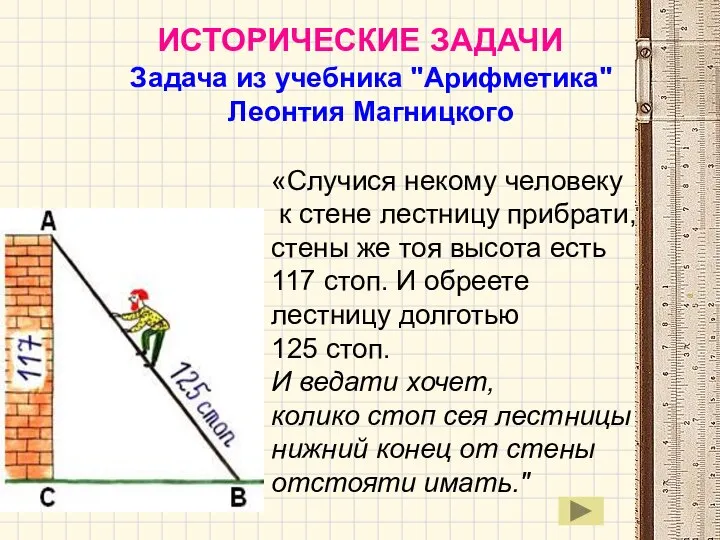
Задача из учебника "Арифметика"
Леонтия Магницкого
«Случися некому человеку
к стене лестницу прибрати, стены же тоя высота есть
117 стоп. И обреете
лестницу долготью
125 стоп.
И ведати хочет,
колико стоп сея лестницы нижний конец от стены отстояти имать."
ИСТОРИЧЕСКИЕ ЗАДАЧИ

Я узнал......
Я научился.....
Мне понравилось......
Мое настроение......

Пребудет вечной истина, как скоро
Её познает слабый человек.
И ныне теорема Пифагора
Верна, как и в далекий век.