Из истории геометрии

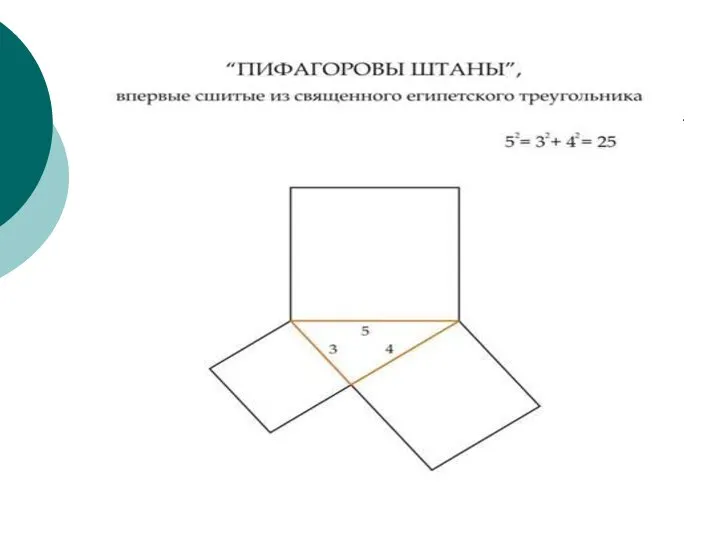
Пифагор
Πυθαγόρας
Дата рождения: прибл. 570 до н. э.
Место рождения: Сидон или Самос
Дата смерти: прим. 490 до н. э.
Место смерти: Метапонт(Италия)
Основные интересы: философия, математика, этика, политика.
Значительные идеи: музыка сфер, Пифагорейский строй, теорема Пифагора.
Оказавшие влияние: Фалес Милетский, Анаксимандр.
Последователи: Евклид, Платон, Кеплер, Гиппас, Филолай.
Бюст Пифагора в Капитолийском музее в Риме.

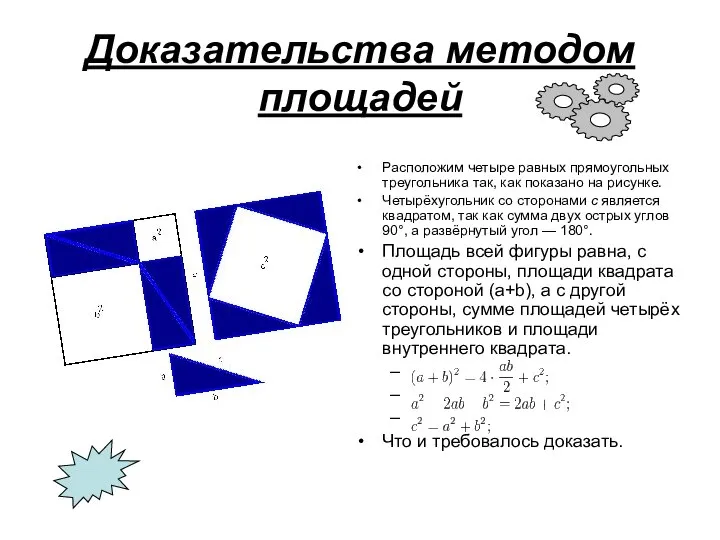
Доказательства методом площадей
Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
Что и требовалось доказать.

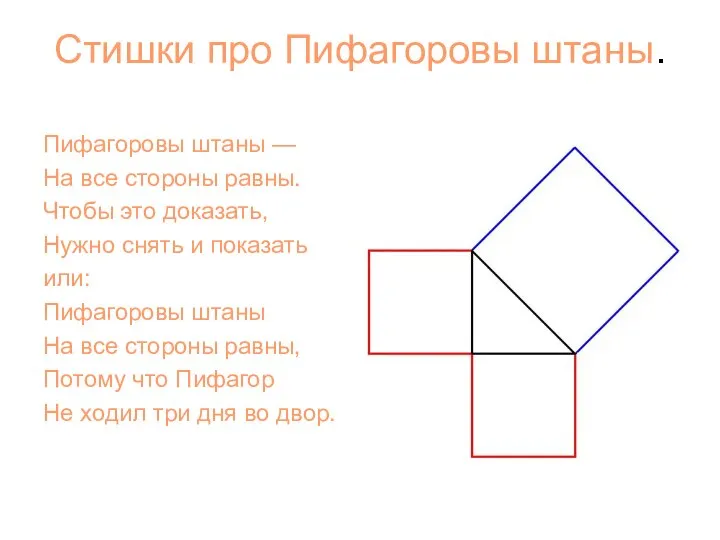
Стишки про Пифагоровы штаны.
Пифагоровы штаны —
На все стороны равны.
Чтобы это доказать,
Нужно снять и показать
или:
Пифагоровы штаны
На все стороны равны,
Потому что Пифагор
Не ходил три дня во двор.

Дерево Пифагора.
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку. Одним из свойств дерева Пифагора является то, что если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Дерево Пифагора.

Обнаженное дерево Пифагора.
Если в классическом дереве Пифагора угол равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора. Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» треугольников, то получается обнаженное дерево Пифагора.
Обнаженное дерево Пифагора