Слайд 2Устная работа
1.Какой плоскости принадлежат точки:
А(-2;0;1), В(3;4;0), С(0;1;-5), Д(0;0;5), Е(0;8;0), М(5;0;0)?
2. АА1 перпендикуляр

к плоскости ХУ, А(2;-3;5). Назвать координаты точки А1.
3. Назвать координаты точки симметричной точке М(3;-4;6) относительно плоскостей ХУ, ХZ, УZ.
4. Найти координаты точки, являющейся серединой отрезка АВ, если А(2;3;7), В(5;-3;7).
5. Какая фигура не имеет плоскость симметрии?
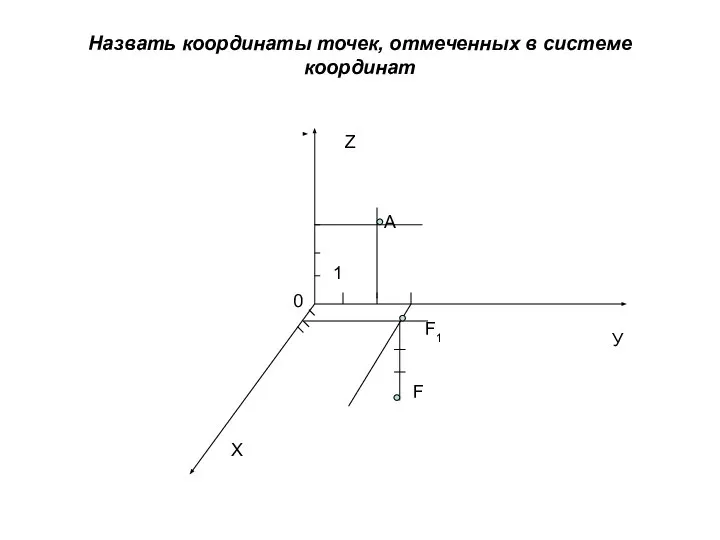
Слайд 3Назвать координаты точек, отмеченных в системе координат
Х
У
Z
F
1
0
F1
А
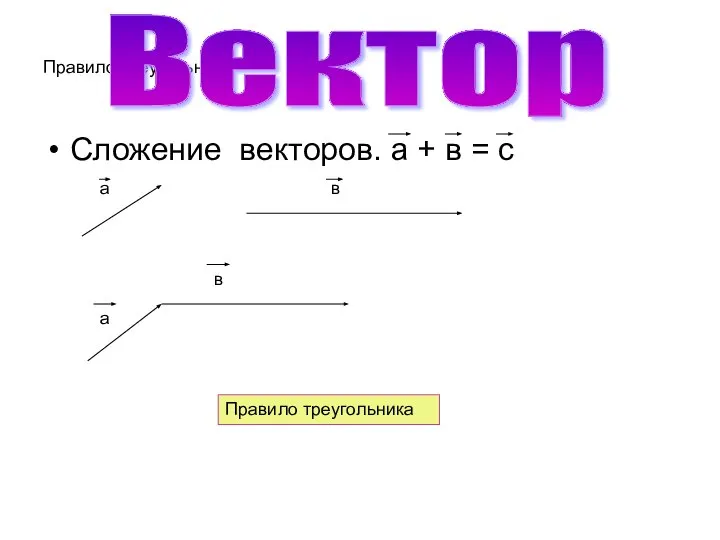
Слайд 4Правило треугольника
Сложение векторов. а + в = с
Вектор
Правило треугольника
а
в
а
в
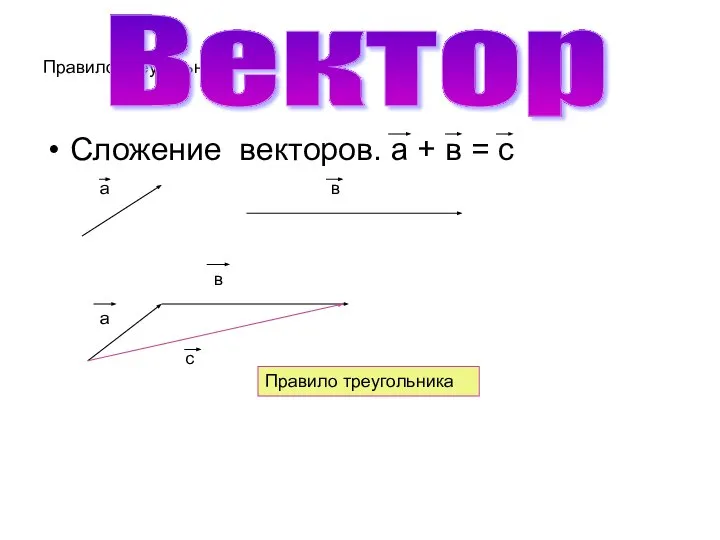
Слайд 5Правило треугольника
Сложение векторов. а + в = с
Вектор
Правило треугольника
а
в
а
в
с
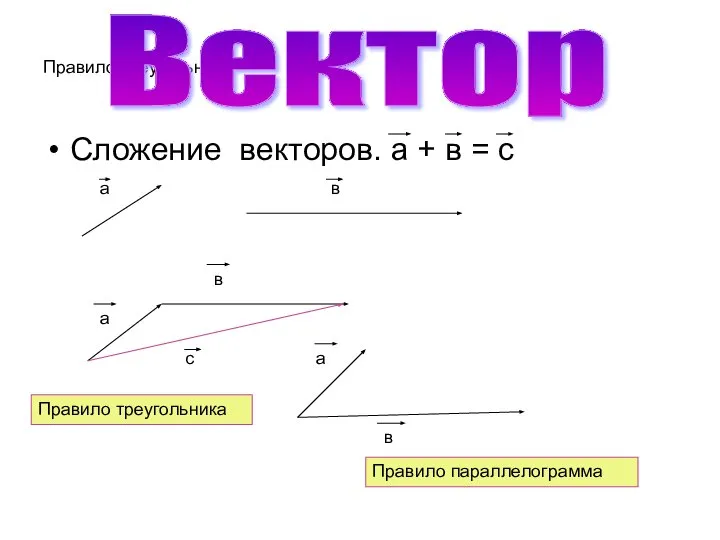
Слайд 6Правило треугольника
Сложение векторов. а + в = с
Вектор
Правило треугольника
Правило параллелограмма
а
в
а
в
с
а
в
Слайд 7Правило треугольника
Сложение векторов. а + в = с
Вектор
Правило треугольника
Правило параллелограмма
а
в
а
в
с
а
в
Слайд 8Правило треугольника
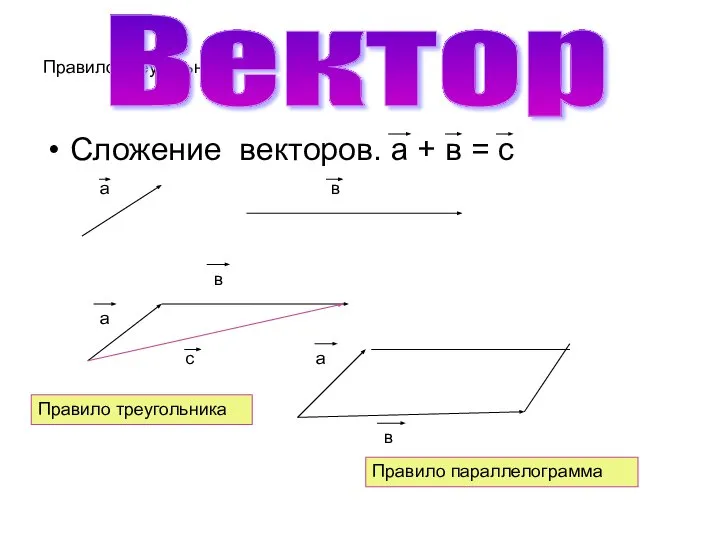
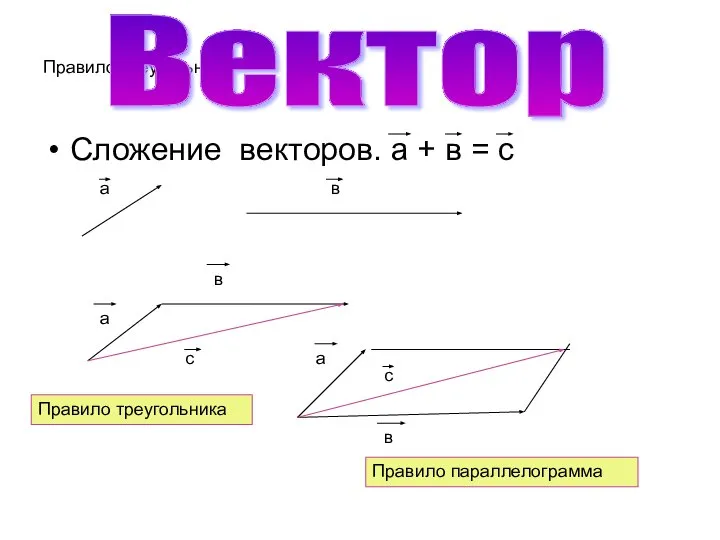
Сложение векторов. а + в = с
Вектор
Правило треугольника
Правило параллелограмма
а
в
а
в
с
а
в
с
Слайд 9а
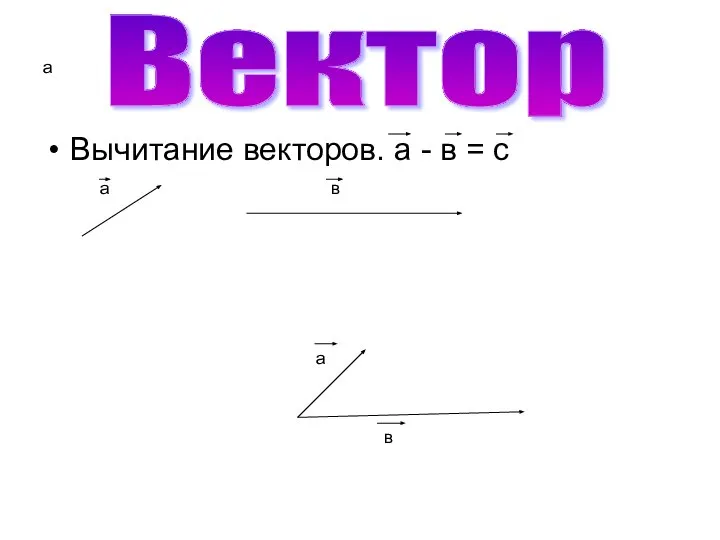
Вычитание векторов. а - в = с
Вектор
а
в
а
в
Слайд 10а
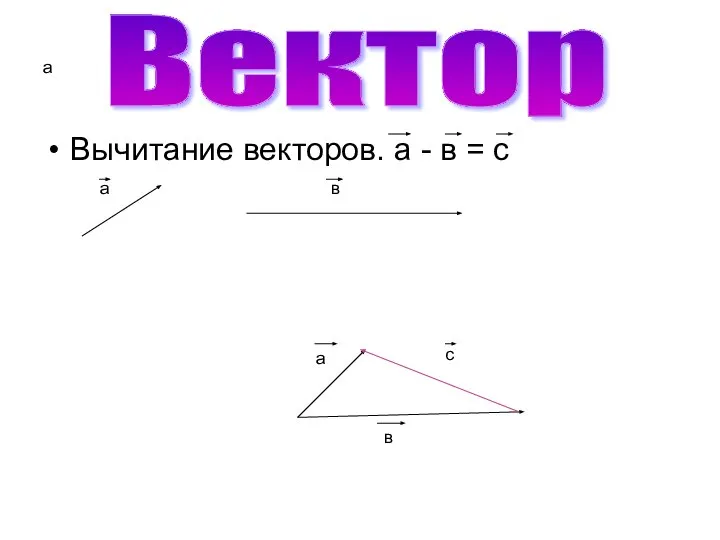
Вычитание векторов. а - в = с
Вектор
а
в
а
в
с
Слайд 11а
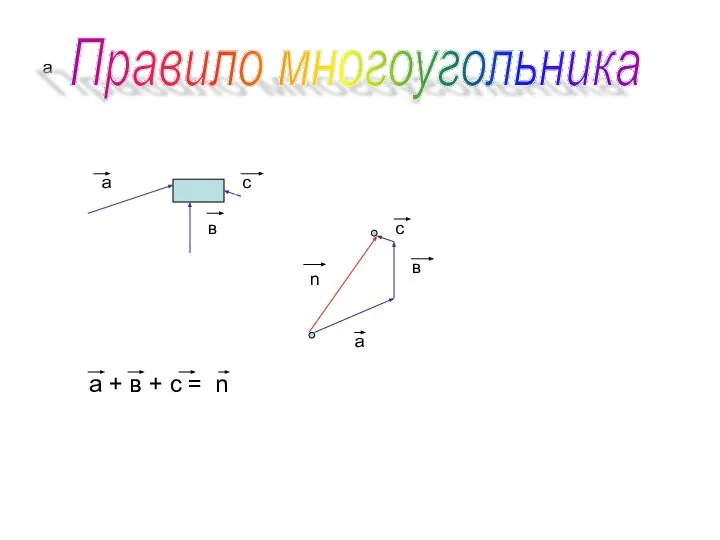
Правило многоугольника
а
в
с
а
в
с
n
а + в + c = n
Слайд 12Сегодня на уроке мы выясним:
1. Как находят координаты вектора.
2. Какие векторы называются

равными.
Слайд 13Тема урока: «Векторы в пространстве»
1. Координаты вектора АВ (х2-х1; у2-у1; z2-z1), если

А(х1;у1;z1), В(х2;у2;z2)
Пример:
А(1;3;6), В(4;7;9). Найти координаты АВ.
Решение:
АВ (4-1; 7-3; 9-6) = АВ (3;4;3)
2. Равенство векторов.
Векторы называются равными, если у них равны координаты.
Пример: А(1;3;6), В(4;7;9), С(7;1;-3), Д(10;5;0)
Решение: АВ (3;4;3), СД (10-7; 5-1; 0-(-3)) = СД (3;4;3). Значит
АВ = СД












 Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет)
Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет) Осевая и центральная симметрии
Осевая и центральная симметрии Презентация на тему Десяток (1 класс)
Презентация на тему Десяток (1 класс)  Задачи на проценты. Схемы
Задачи на проценты. Схемы LP
LP Координатная плоскость (урок 3)
Координатная плоскость (урок 3) Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла
Презентация на тему Прямоугольный треуголиник: синус, косинус, тангенс угла  Определенный интеграл. Пример 2. Лекция
Определенный интеграл. Пример 2. Лекция 6. Анімаційна гра. Квадрат. Знайди правильний варіант відповіді
6. Анімаційна гра. Квадрат. Знайди правильний варіант відповіді Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс Использование Интернет-сервисов на уроках математики
Использование Интернет-сервисов на уроках математики Решение иррациональных уравнений с параметром
Решение иррациональных уравнений с параметром Математический диктант
Математический диктант Функции нескольких переменных
Функции нескольких переменных Решение задач с помощью пропорции. 5 класс
Решение задач с помощью пропорции. 5 класс Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Десятичнвя дробь в виде смешанного числа
Десятичнвя дробь в виде смешанного числа Презентация на тему Усеченный конус
Презентация на тему Усеченный конус  Карточки по математике
Карточки по математике Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Циклоида, эпициклоида
Циклоида, эпициклоида Элементы теории графов
Элементы теории графов Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс Произведение дробей, обратных друг другу
Произведение дробей, обратных друг другу Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Математическая статистика 2
Математическая статистика 2 Естественный отбор. Бинарный урок по биологии и математике (часть 1)
Естественный отбор. Бинарный урок по биологии и математике (часть 1) Геометрия и искусство
Геометрия и искусство