Содержание
- 2. В настоящее время в науке и инженерной практике широко используется метод математического моделирования. Математическим моделированием называется
- 4. Сложные модели описывают объект точнее (адекватнее). Математическое моделирование позволило исследовать на ЭВМ очень сложные процессы, такие,
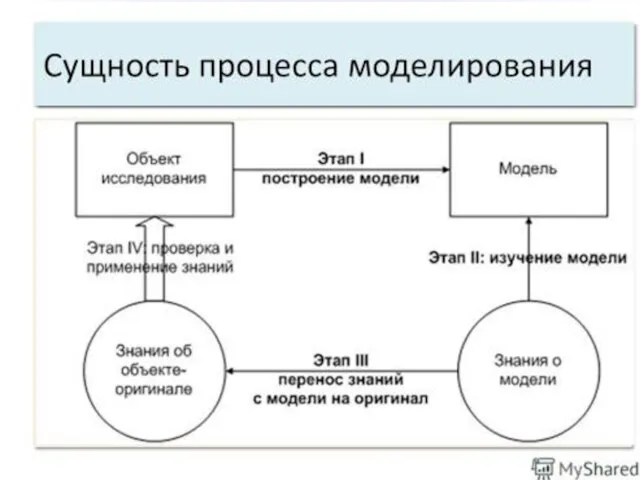
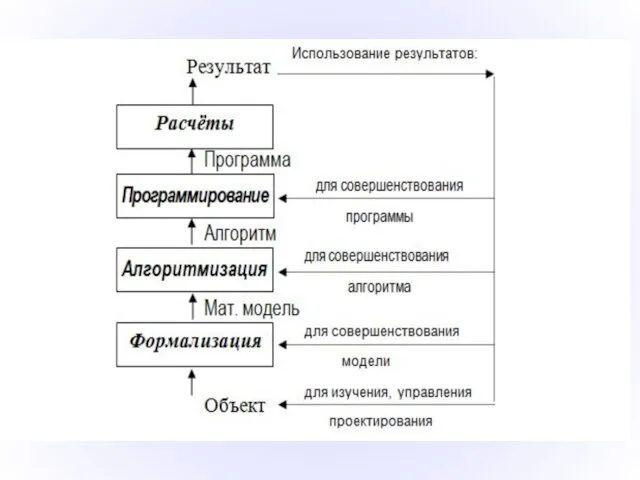
- 5. Основные этапы математического моделирования: Разработка модели – формализация. Изучается в прикладных и фундаментальных науках. Разработка метода
- 7. Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом
- 8. вычисления x*:
- 13. Специфика вычислительной математики Предмет вычислительной математики. Погрешности. Численное дифференцирование. Вычислительная математика имеет дело не только с
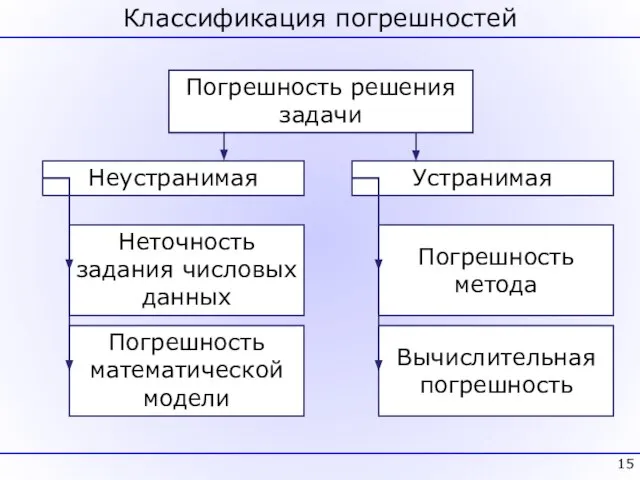
- 14. Классификация погрешностей
- 15. Классификация погрешностей Погрешность решения задачи Неустранимая Устранимая Неточность задания числовых данных Погрешность математической модели Погрешность метода
- 16. Пример – колебания математического маятника ΔΣ = | φ3 – φ | = | φ3 –
- 17. Вычислительная погрешность Утверждение 1.1. Относительная погрешность округления при представлении вещественного числа в ЭВМ ε ≈ 2–t,
- 18. Иллюстрация понятия вычислительной погрешности (1) Приближенное вычисление значения синуса с помощью разложения в ряд Тейлора Ряд
- 19. #define EPS 1.e-8 #define X 0.52366 ... int i, k = 0; double curr_sum = 0.0,
- 21. Скачать презентацию















 ЧМ МНП. Занятие 1 (магистры ФН)
ЧМ МНП. Занятие 1 (магистры ФН) Производная вокруг нас
Производная вокруг нас Комплексные числа
Комплексные числа Случайные величины. Таблицы распределения
Случайные величины. Таблицы распределения Задачи на концентрацию
Задачи на концентрацию Свойства функций. Монотонность
Свойства функций. Монотонность Дифференциальные уравнения
Дифференциальные уравнения Понятия длиннее, короче, одинаковые по длине
Понятия длиннее, короче, одинаковые по длине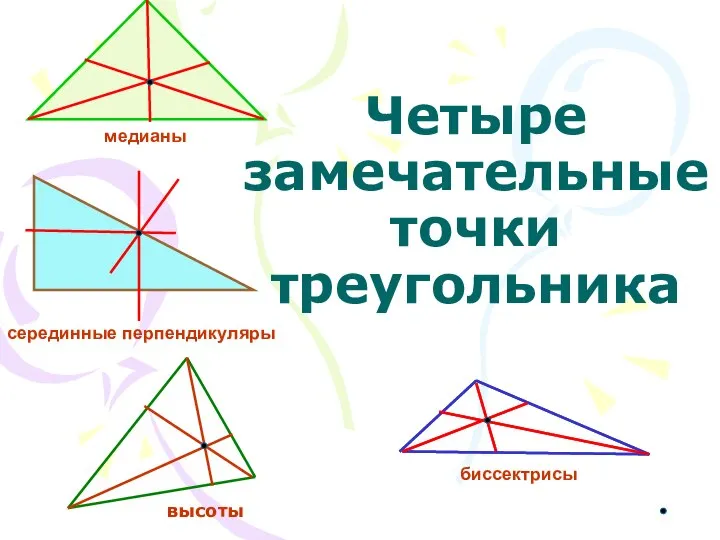 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Определители матриц
Определители матриц Состав числа 10
Состав числа 10 Тестирование
Тестирование Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ
Презентация на тему ТАБЛИЦА УМНОЖЕНИЯ  Влияние математических действий на аликвоты
Влияние математических действий на аликвоты Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Закрепление сложения однозначных чисел с переходом через десяток
Закрепление сложения однозначных чисел с переходом через десяток Преобразование графиков функций, содержащих модуль
Преобразование графиков функций, содержащих модуль Решение тригонометрических уравнений, приводимых калгебраическим
Решение тригонометрических уравнений, приводимых калгебраическим Умножение дробей
Умножение дробей Решение задач
Решение задач Графики элементарных функций
Графики элементарных функций Основы математических знаний. Часть 3. Лучше гор могут быть только горы!
Основы математических знаний. Часть 3. Лучше гор могут быть только горы! Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Равнобедренный треугольник. Свойства равнобедренного треугольника
Равнобедренный треугольник. Свойства равнобедренного треугольника Система двух случайных величин. Многомерные СВ
Система двух случайных величин. Многомерные СВ Точечные и интервальные оценки
Точечные и интервальные оценки Математика в лицах. Пифагор Самосский
Математика в лицах. Пифагор Самосский