Содержание
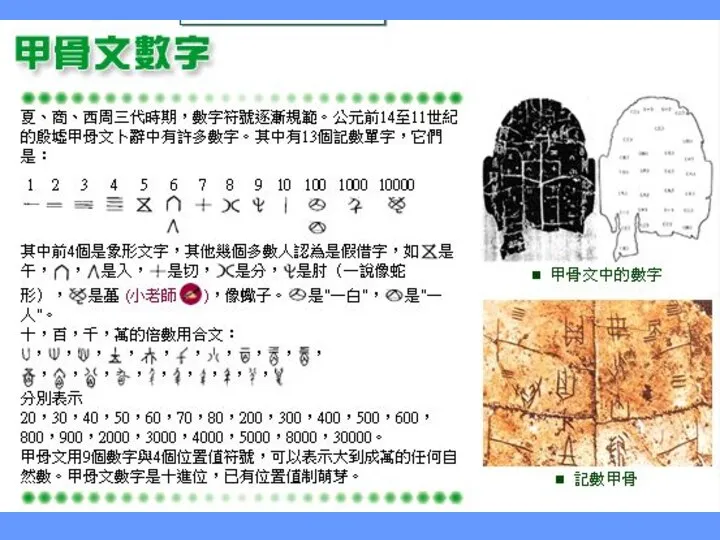
- 2. Цзягувэнь 甲骨文 Архаическая династия Шан-Инь «殷商» (商朝 殷代 XVI – XI вв. до н. э. 1600
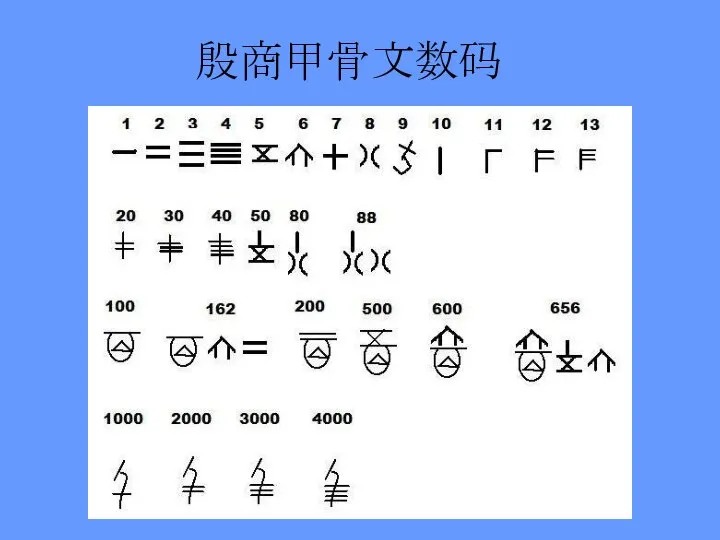
- 5. 殷商甲骨文数码
- 6. Чжан Хэн (張衡 公元78年-139年) Рассчитал π (юань чжоу люй 圓周率): 1. 92/29 ≈ 3,1724 2. Корень
- 7. Лю Хуэй 劉徽 (公元225年-295年) Жил в эпоху Троецарствия (Саньго三國 220-280) Цао Вэй 曹魏 劉徽 Лю Хуэй
- 8. Цзючжан суаньшу 九章算術 «Математика в девяти книгах» 246 задач Напр. 粟米 Су ми, «Соотношение злаков» —
- 9. Лю Хуэй 劉徽 (公元225年-295年) Расчёт числа π методом вписанных правильных многоугольников. Решение систем линейных уравнений методом,
- 10. Лю Хуэй 劉徽 (公元225年-295年) Алгоритм расчёта π (краткое описание) 刘徽割圆术是建立在圆面积论的基础之上的。他首先论证,将圆分割成多边形,分割来越细,多边形的边数越多,多边形的面积就和圆面积没有差别了。他说,将6边形一边的长度乘以圆半径,再乘3,得12边形的面积。将12边形的一边长乘半径,再乘6,得24边形面积。越割越细,多边形和圆面积的差越小。如此割了再割,最后终于和圆合为一体,毫无差别了[4]。 6边形的面积显然和圆面积相差很多。 内接正12边形面积 = 6边形面积+6个蓝色三角形面积,向圆面积趋近了一步。 正24边形面积=6边形面积+6个蓝色三角形面积+12个黄色三角形面积,更加接近圆面积了。 显然:
- 11. Цзу Чунчжи 祖沖之(公元429年-500年) Китайский математик и астроном. Начальник уезда
- 12. Цзу Чунчжи 祖沖之(公元429年-500年) Расчитал продолжительность года в 365.24281481 дней (сейчас подсчитана 365.24219878 дней)
- 13. Ми люй 密率 355/113 «Приближённое значение» π (юань чжоу люй 圓周率) Цзу Чунчжи 祖沖之(公元429年-500年)
- 14. Цзу Чунчжи 祖沖之(公元429年-500年) Юэ люй 約率 22/7 «Приближённое значение» π (юань чжоу люй 圓周率)
- 17. Скачать презентацию






![Лю Хуэй 劉徽 (公元225年-295年) Алгоритм расчёта π (краткое описание) 刘徽割圆术是建立在圆面积论的基础之上的。他首先论证,将圆分割成多边形,分割来越细,多边形的边数越多,多边形的面积就和圆面积没有差别了。他说,将6边形一边的长度乘以圆半径,再乘3,得12边形的面积。将12边形的一边长乘半径,再乘6,得24边形面积。越割越细,多边形和圆面积的差越小。如此割了再割,最后终于和圆合为一体,毫无差别了[4]。 6边形的面积显然和圆面积相差很多。 内接正12边形面积](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1165097/slide-9.jpg)





 Векторы. 9 класс
Векторы. 9 класс Формула объема пирамиды
Формула объема пирамиды Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Все действия с рациональными дробями. Подготовка к контрольной работе
Все действия с рациональными дробями. Подготовка к контрольной работе Формула у=х2
Формула у=х2 Многочлен. Стандартный вид многочлена. Степень многочлена
Многочлен. Стандартный вид многочлена. Степень многочлена Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Геометрия. Построение
Геометрия. Построение Евклидова геометрия
Евклидова геометрия Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем Измерение площади с помощью палетки. 4 класс
Измерение площади с помощью палетки. 4 класс Вторая производная и ее физический смысл
Вторая производная и ее физический смысл Отношения и пропорция
Отношения и пропорция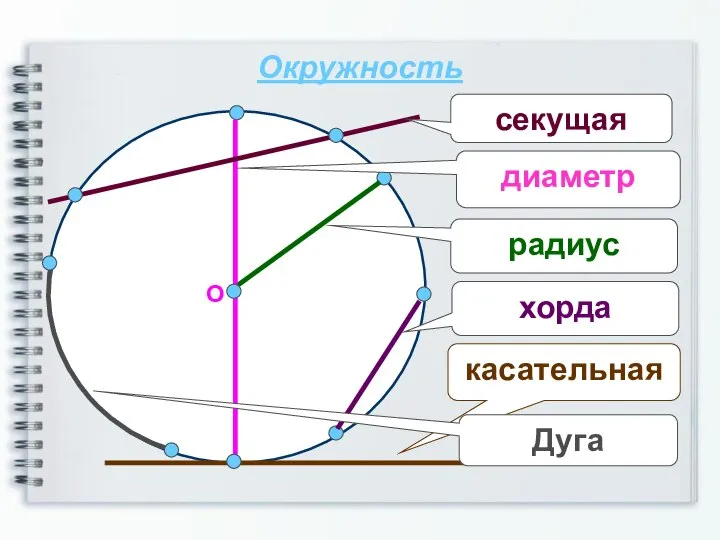 Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1)
Д.з. на 16.09 Углы и отрезки, связанные с окружностью (1) Теорема о площади треугольников
Теорема о площади треугольников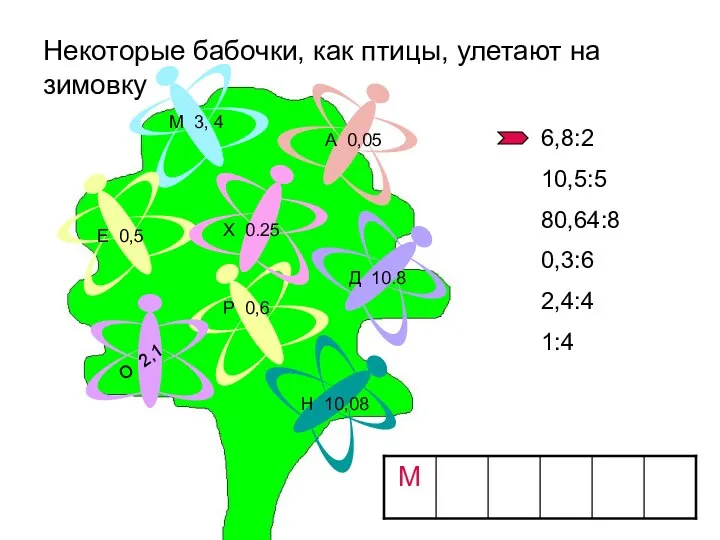 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Тела вращения. Урок 142
Тела вращения. Урок 142 Веселая математика. Головоломки
Веселая математика. Головоломки Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Методы расчета КИХ-фильтров
Методы расчета КИХ-фильтров Коррекция нелинейных систем
Коррекция нелинейных систем Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са
Урок математики во 2 классе «Устные приемы вычислений в пределах 100» Выполнила: учитель начальных классов МОУ «СОШ № 43» Города Са Решение неполных квадратных уравнений
Решение неполных квадратных уравнений Планирование эксперимента
Планирование эксперимента Консультация ДУ
Консультация ДУ