Окружность и прямая

С
D
P
E
Прямые РЕ и СD - параллельные прямые
Какие прямые называются параллельными?
Ответьте на следующие вопросы:

А
E
В
К
Какие прямые называются перпендикулярными?

Какие прямые, по вашему мнению, параллельны?
a
b
c
d
n
m
k

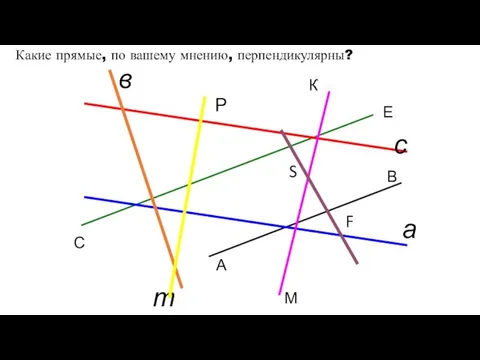
а
с
т
А
В
С
Е
М
К
Р
F
S
в
Какие прямые, по вашему мнению, перпендикулярны?

Расстоянием от точки A до прямой a называется длина перпендикуляра AH, проведенного из точки к прямой.
Расстояние от точки до прямой – наименьшее из расстояний от этой точки до точек прямой.
Что называют расстоянием от точки до прямой?
A
H
M
a

О
Окружность

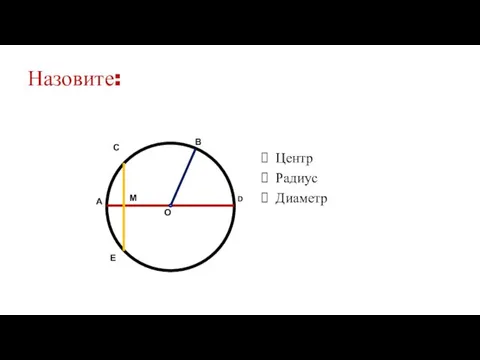
Назовите:
Центр
Радиус
Диаметр
Е
О
В
D
М
А
С

Взаимное расположение прямой и окружности
r
ОВ > ОА
Окружность и прямая не имеют общих точек
А
В
d

Взаимное расположение прямой и окружности
В
r
ОВ < ОА
Окружность и прямая имеют две общие точки.
Прямая называется секущей по отношению к окружности.
А
d

Взаимное расположение прямой и окружности
В
r
ОВ = ОА
Окружность и прямая имеют одну общую точку.
Прямая называется касательной по отношению к окружности.
А
d

А
О
d
На этом свойстве основан способ построения касательной к окружности.
Построим прямую d, перпендикулярную радиусу ОА и проходящую через точку А.
Построим касательную к окружности в этой точке:
Проведём радиус ОА,
Прямая d- касательная к окружности в точке А.

Свойство касательной:
Касательная перпендикулярна к радиусу, проведенному в точку касания.
d – касательная к окружности с центром О
A – точка касания
OA - радиус
O
A
d