Содержание
- 2. Из истории комбинаторики С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением
- 3. Комбинаторика – это раздел математики, в котором изучаются различные соединения (комбинации) элементов конечных множеств. Выбором объектов
- 4. Элементарные комбинаторные конфигурации: сочетания, размещения, перестановки. Для подсчета числа этих конфигураций используются правила суммы и произведения
- 5. Если некоторый объект a можно выбрать n1 способами, а объект в можно выбрать n2 способами, причем
- 6. Пример1. Имеется 8 шаров: в 1 ящик положили 5 шт., а во 2 ящик - 3
- 7. Правило умножения
- 8. Пример 2. На входной двери дома установлен домофон, на котором нанесены цифры 0,1,2,…9.Каждая квартира получает кодовый
- 9. Правило включения-исключения Пусть у множества А и В общая часть насчитывает k элементов Тогда в объединении
- 10. Пример3. В группе каждый студент занимается в спортивной секции. При этом 20 студентов занимаются волейболом, 12
- 11. Размещения
- 12. Обозначение: ⎯ читают «А из эн по k»
- 13. Сколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что
- 14. Сколькими способами можно обозначить данный вектор, используя буквы A, B, C, D? Решение: Действительно, это наборы
- 15. Перестановки
- 16. Перестановками из n элементов называются соединения (комбинации), которые состоят из одних и тех же n элементов
- 17. Задача 2. Даны цифр: 1,2,3,4,5,6,7. Сколько различных семизначных чисел можно составить из этих цифр? Каждое число
- 18. Сочетания
- 20. Решение Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом,
- 22. Различие между перестановками, размещениями, сочетаниями В случае перестановок берутся все элементы и изменяется только их местоположение.
- 23. Схема выбора с возвращением
- 24. Перестановки с повторениями. Пусть в множестве из n элементов есть k различных типов элементов, при этом
- 26. Размещения с повторениями. Если при упорядоченной выборке k элементов из n элементов возвращаются обратно, то полученные
- 27. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить
- 29. Скачать презентацию







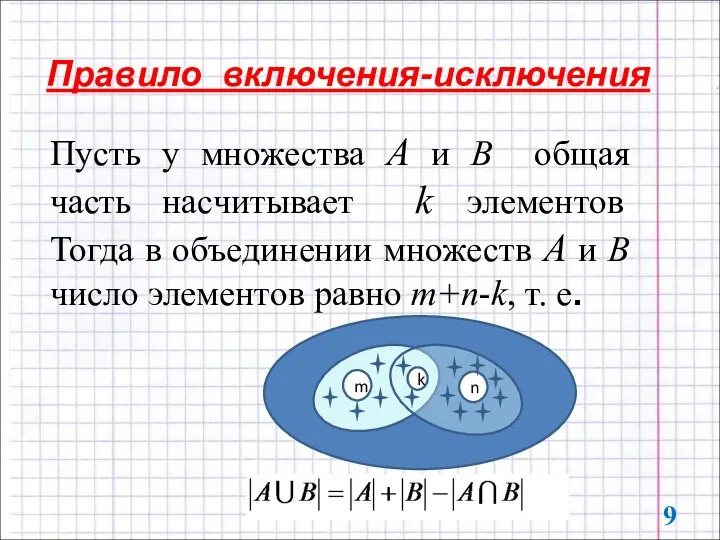














 Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2 Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Математическое описание случайных явлений
Математическое описание случайных явлений Операции над множествами
Операции над множествами Презентация на тему Занимательная математика (5 класс)
Презентация на тему Занимательная математика (5 класс)  Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр Упрощение выражений
Упрощение выражений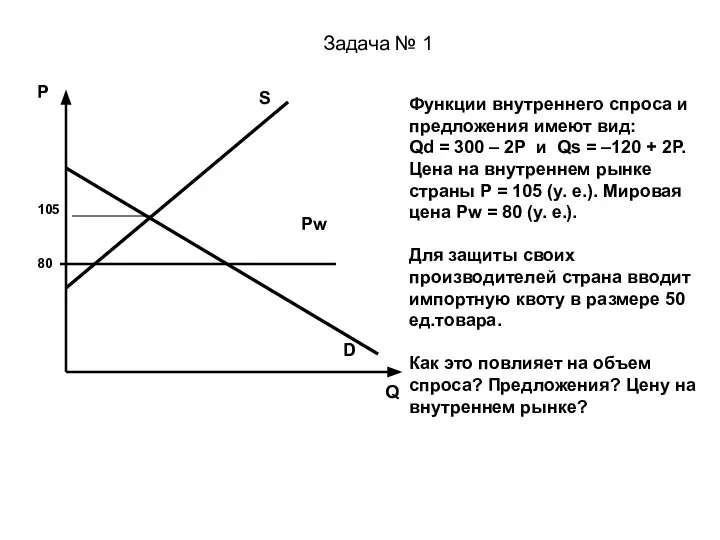 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Математика в профессии сварщика
Математика в профессии сварщика Задачи на перебор вариантов
Задачи на перебор вариантов Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Прямоугольные треугольники
Прямоугольные треугольники История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.
Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г. Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Математика в медицине
Математика в медицине Векторное произведение векторов
Векторное произведение векторов