Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса
Содержание
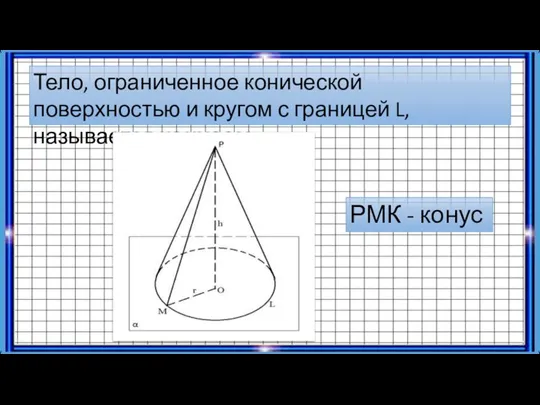
- 2. Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. РМК - конус
- 3. Круг называется основанием конуса, вершина конической поверхности — вершиной конуса, отрезки образующих, заключенные между вершиной и
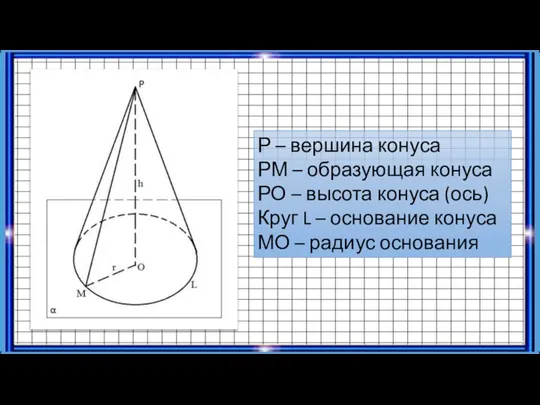
- 4. Р – вершина конуса РМ – образующая конуса РО – высота конуса (ось) Круг L –
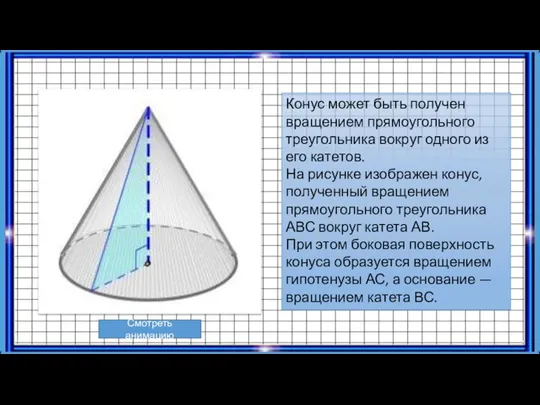
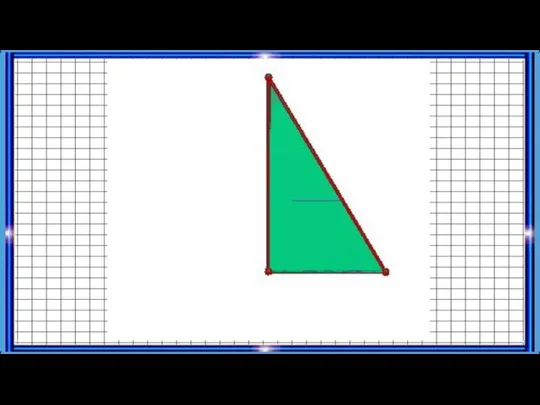
- 5. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке изображен конус,
- 7. Сечения конуса Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание
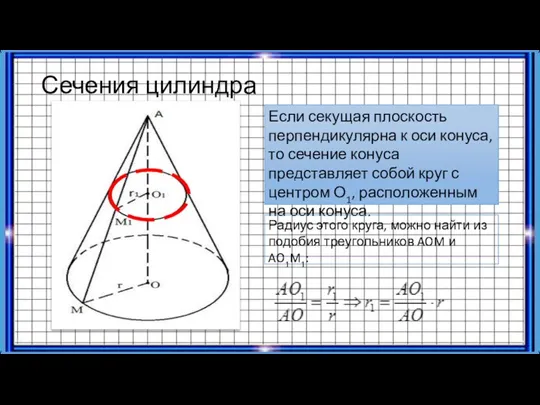
- 8. Сечения цилиндра Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с
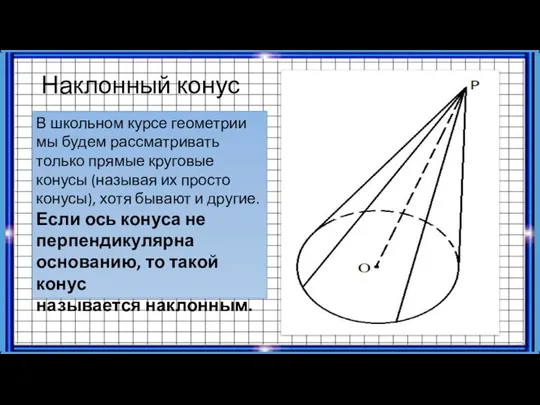
- 9. Наклонный конус В школьном курсе геометрии мы будем рассматривать только прямые круговые конусы (называя их просто
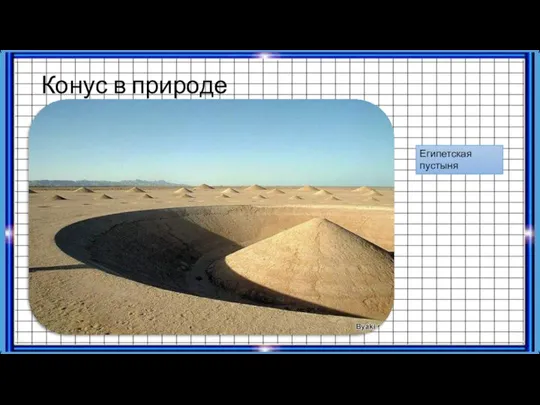
- 10. Конус в природе Египетская пустыня
- 11. Конус в природе
- 12. Конус в архитектуре Библиотека Делфотского технического университета, Южная Голландия, Нидерланды.
- 13. Конус в архитектуре Midrand Water Tower, South Africa На 6 000 000 литров — крупнейшая водонапорная
- 14. Конус в архитектуре «Вигвам» – название американской сети мотелей с уникальными номерами в форме типи. Они
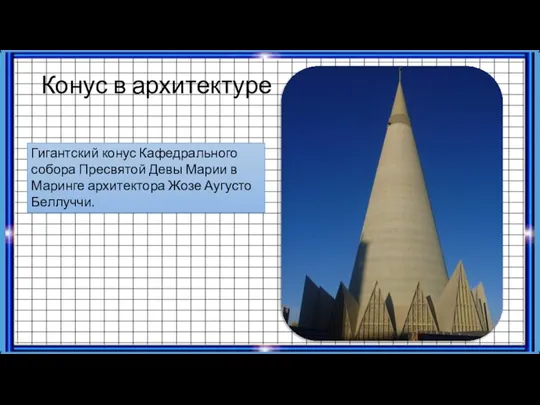
- 15. Конус в архитектуре Гигантский конус Кафедрального собора Пресвятой Девы Марии в Маринге архитектора Жозе Аугусто Беллуччи.
- 16. Конус в жизни Солнечная электростанция из конусов
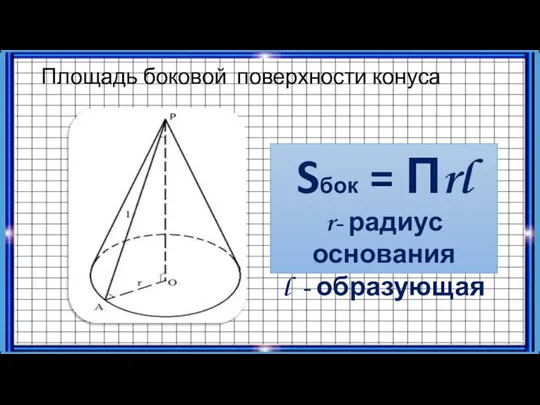
- 17. Площадь боковой поверхности конуса Sбок = Пrl r- радиус основания l - образующая
- 18. Площадь полной поверхности конуса Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Так
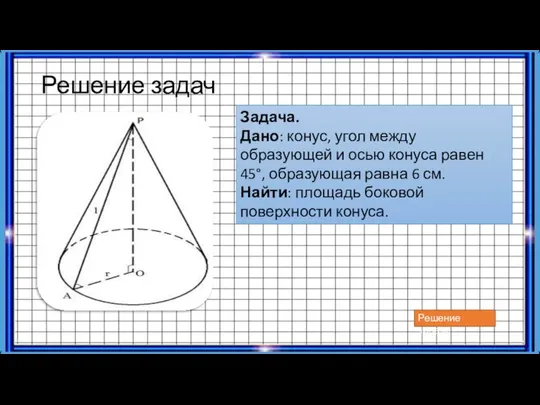
- 19. Решение задач Задача. Дано: конус, угол между образующей и осью конуса равен 45°, образующая равна 6
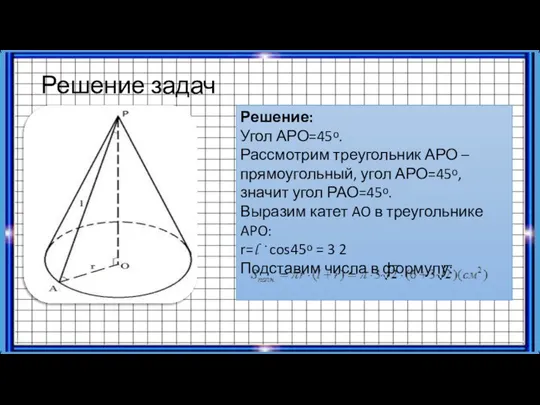
- 20. Решение задач Решение: Угол АРО=45ᵒ. Рассмотрим треугольник АРО – прямоугольный, угол АРО=45ᵒ, значит угол РАО=45ᵒ. Выразим
- 21. Список источников содержания и иллюстраций Геометрия: учеб. для 10 - 11 кл. для общеобразовательных учреждений: базовый
- 23. Скачать презентацию








 Геометрия в живописи
Геометрия в живописи Теория вероятностей
Теория вероятностей Условный оператор задач
Условный оператор задач Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Время. Решение задач
Время. Решение задач Математика вокруг нас
Математика вокруг нас Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен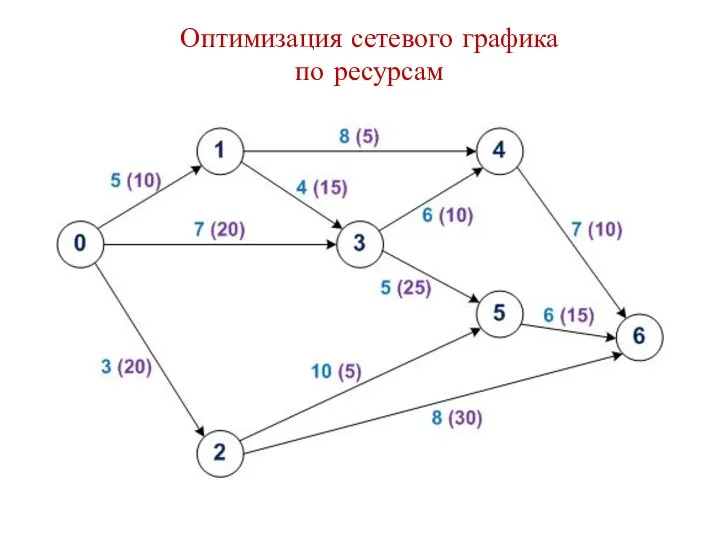 Оптимизация сетевого графика по ресурсам
Оптимизация сетевого графика по ресурсам Построение сечений
Построение сечений Тела вращения. Использование ИКТ
Тела вращения. Использование ИКТ МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ Ломаная линия. Обозначение ломаной
Ломаная линия. Обозначение ломаной Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Арифметическая прогрессия
Арифметическая прогрессия Задания Незнайки
Задания Незнайки Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Делимость чисел. НОК
Делимость чисел. НОК Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Презентация на тему Длина окружности и площадь круга (9 класс)
Презентация на тему Длина окружности и площадь круга (9 класс)  Параллельный перенос
Параллельный перенос Действия с дробями. Устная работа
Действия с дробями. Устная работа Первый признак параллельности прямых
Первый признак параллельности прямых Презентация на тему Перестановка слагаемых (1 класс)
Презентация на тему Перестановка слагаемых (1 класс)  Натуральные числа и их обозначение
Натуральные числа и их обозначение Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Это полезно знать
Это полезно знать Выражение отношения в процентах
Выражение отношения в процентах Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс