Содержание
- 2. Стереометрия изучает свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео»
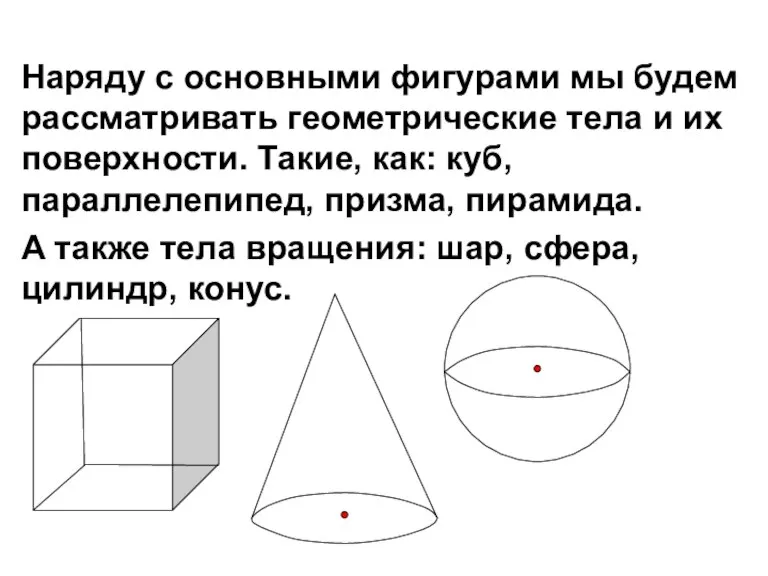
- 3. Наряду с основными фигурами мы будем рассматривать геометрические тела и их поверхности. Такие, как: куб, параллелепипед,
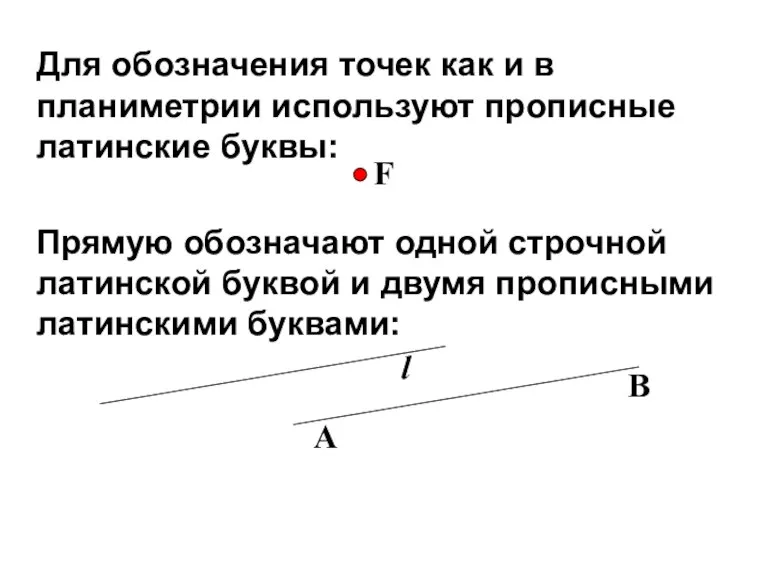
- 4. Для обозначения точек как и в планиметрии используют прописные латинские буквы: Прямую обозначают одной строчной латинской
- 5. Плоскость в стереометрии обозначают греческими буквами, например: А на рисунках чаще всего плоскость изображают в виде
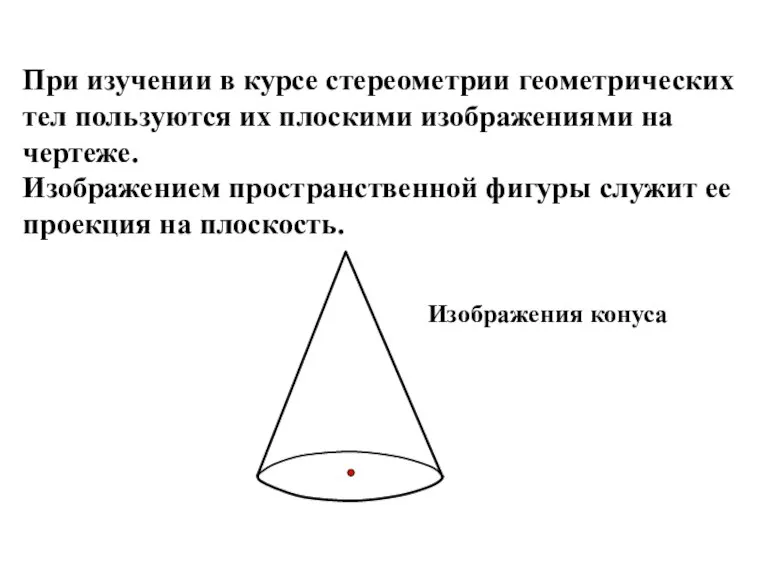
- 6. При изучении в курсе стереометрии геометрических тел пользуются их плоскими изображениями на чертеже. Изображением пространственной фигуры
- 7. Изучая свойства геометрических фигур – воображаемых объектов, мы получаем представление о геометрических свойствах реальных предметов (их
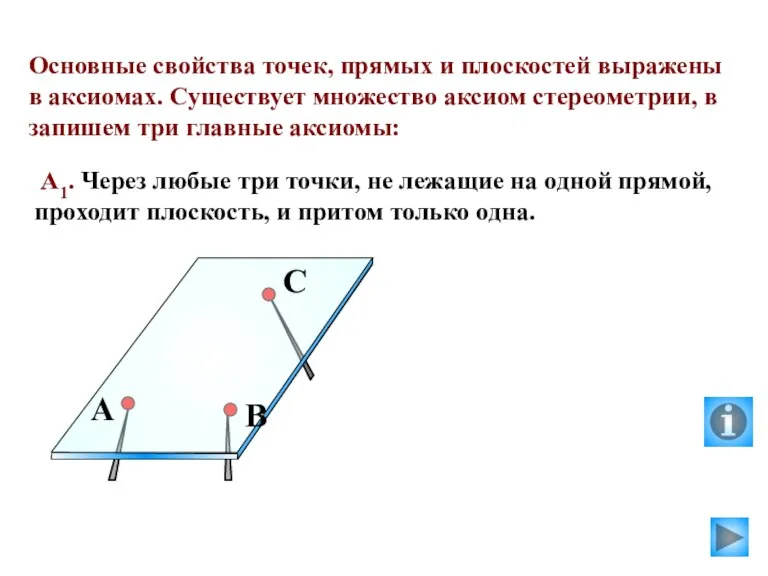
- 8. Основные свойства точек, прямых и плоскостей выражены в аксиомах. Существует множество аксиом стереометрии, в запишем три
- 9. Самый простой пример к аксиоме А1 из повседневной жизни: Для устойчивого положения табуретки достаточно три точки
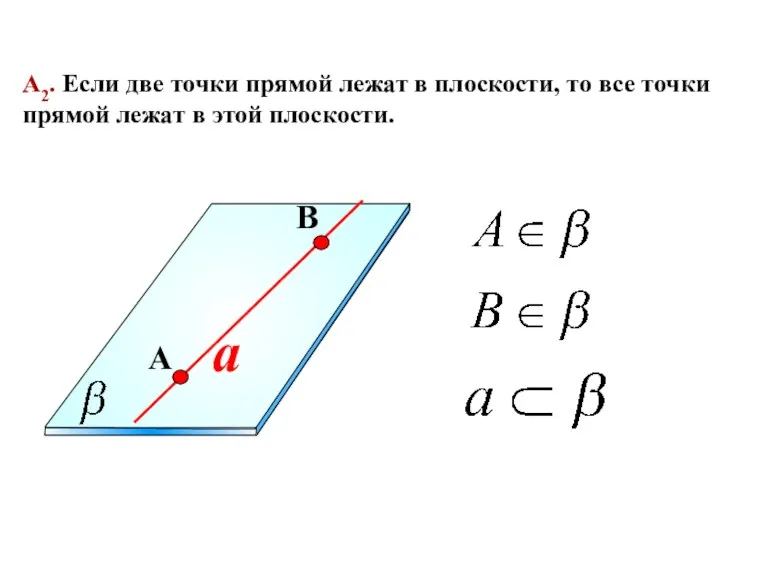
- 10. a А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой
- 11. Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки. Линейку прикладывают краем к плоской
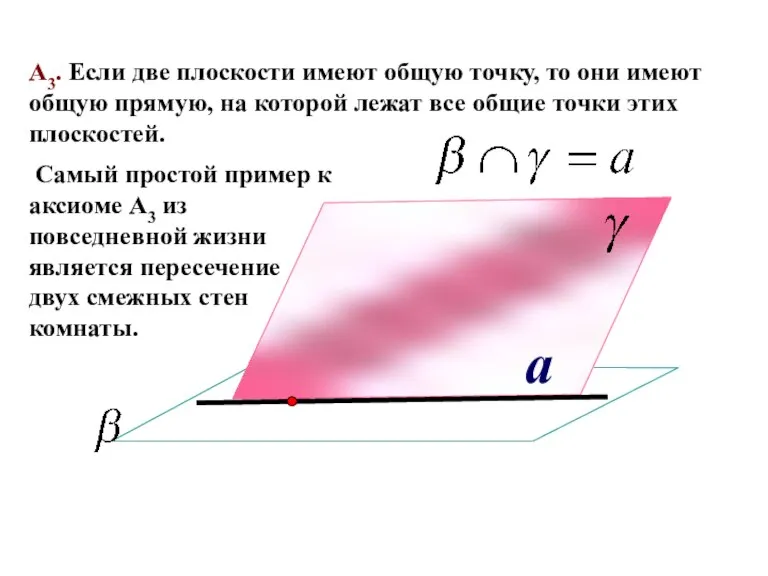
- 12. a А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
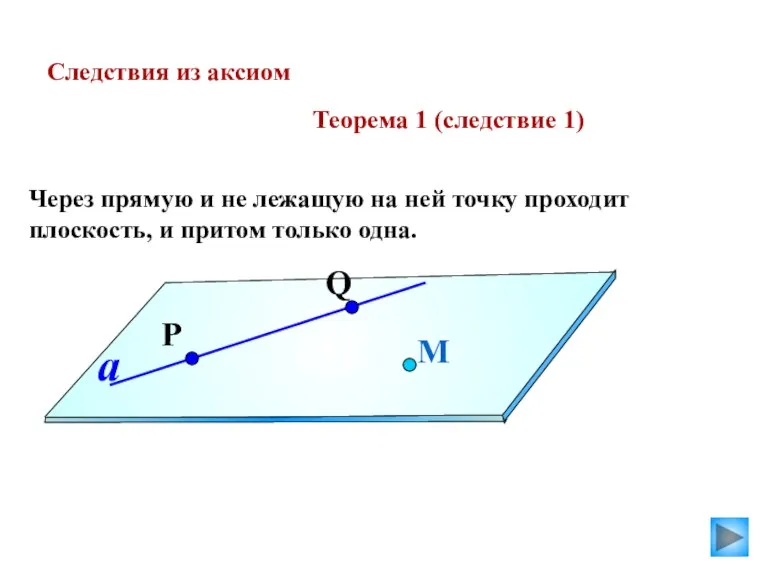
- 13. Следствия из аксиом Теорема 1 (следствие 1) Через прямую и не лежащую на ней точку проходит
- 15. Скачать презентацию





 Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Нахождение числа по его дроби. Урок-игра Детективное агентство
Нахождение числа по его дроби. Урок-игра Детективное агентство Решение линейных неравенств
Решение линейных неравенств Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45 Уравнение прямой на координатной плоскости
Уравнение прямой на координатной плоскости Презентация на тему Измерение высоты предмета
Презентация на тему Измерение высоты предмета  Интеграл. Формула Ньютона-Лейбница
Интеграл. Формула Ньютона-Лейбница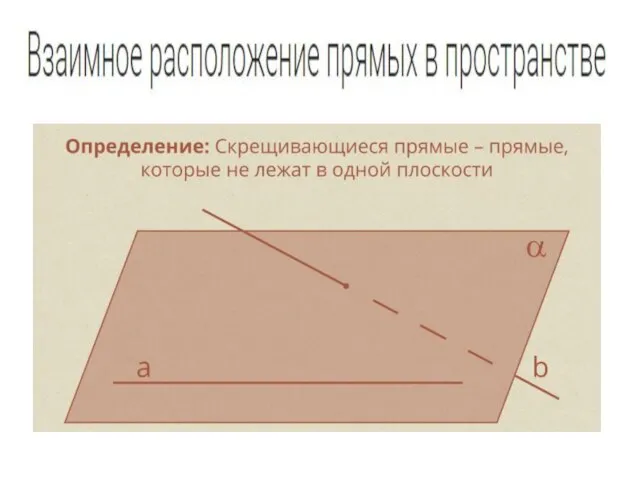 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Деревья
Деревья Пересечение высот
Пересечение высот Проценты (5)
Проценты (5) Виды графов. Тема 4.2
Виды графов. Тема 4.2 Как построена задача, какие части есть в задаче
Как построена задача, какие части есть в задаче Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Представьте в виде неправильной дроби
Представьте в виде неправильной дроби Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Теорема Пифагора
Теорема Пифагора Проецирование правильной шестиугольной призмы
Проецирование правильной шестиугольной призмы Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Задачи на площадь
Задачи на площадь Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Точка. Кривая линия. Прямая линия. Отрезок
Точка. Кривая линия. Прямая линия. Отрезок Позиция 7 ЕГЭ 2016. Физический смысл производной
Позиция 7 ЕГЭ 2016. Физический смысл производной Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Моменты случайной величины
Моменты случайной величины mypresentation.ru
mypresentation.ru Задачи на умножение. 2 класс
Задачи на умножение. 2 класс Уровень и отвес
Уровень и отвес