Слайд 2Определенный интеграл
– формула Ньютона-Лейбница.
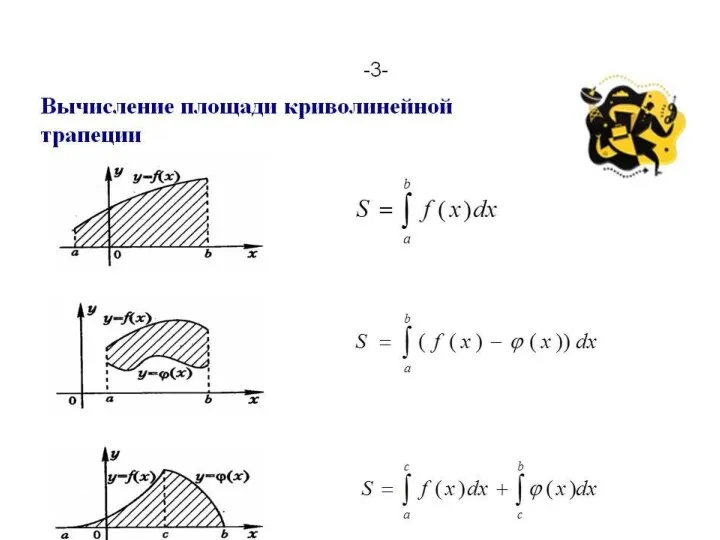
Геометрический смысл определенного интеграла заключается в том, что определенный

интеграл равен площади криволинейной трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.
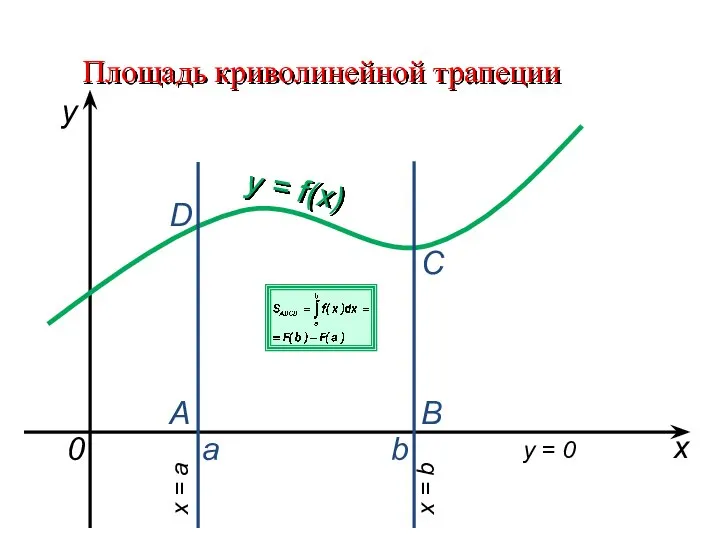
Слайд 3Площадь криволинейной трапеции
a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y = 0
Слайд 4Площадь криволинейной трапеции (1)
a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =
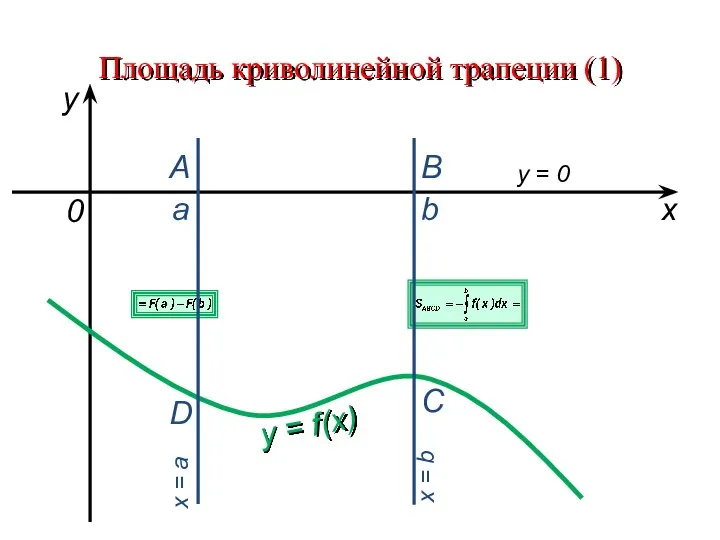
0
Слайд 5a
b
x
y
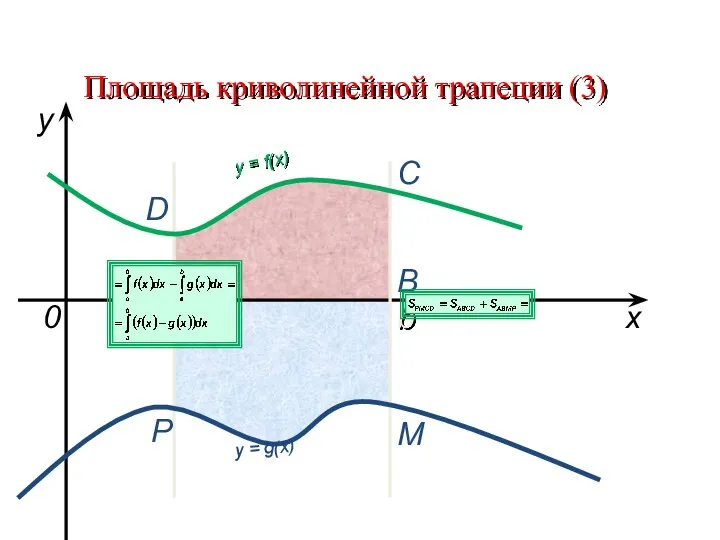
y = f(x)
0
y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (3)
Слайд 6Пример 1:
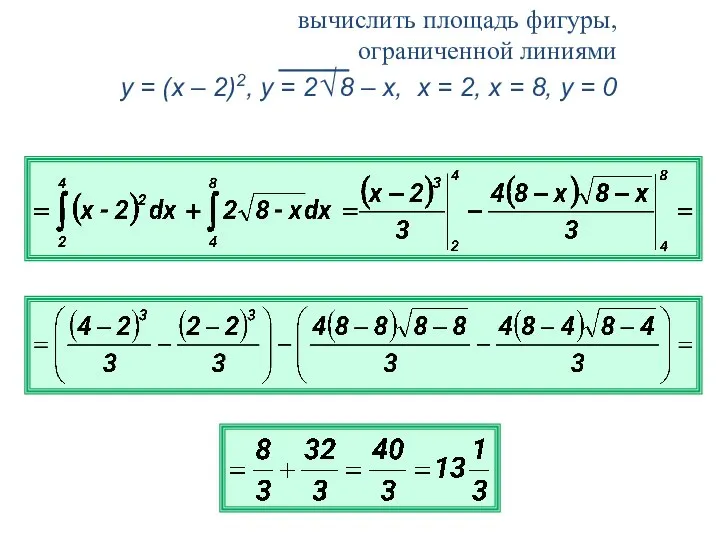
вычислить площадь фигуры,
ограниченной линиями y = x2, y = x
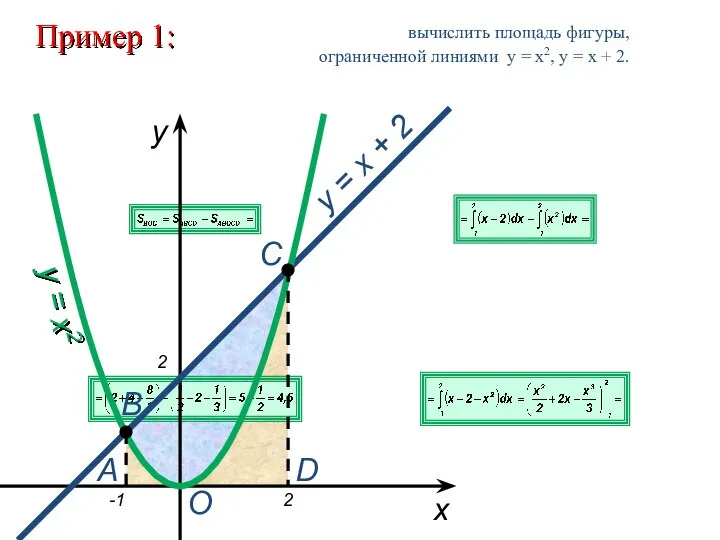
+ 2.
x
y
y = x2
y = x + 2
-1
2
A
B
O
D
C
2
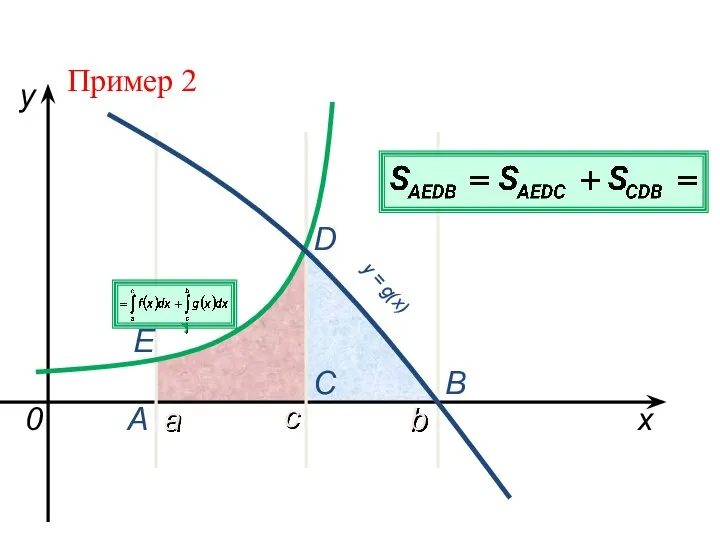
Слайд 7a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D
с
Е
Пример 2
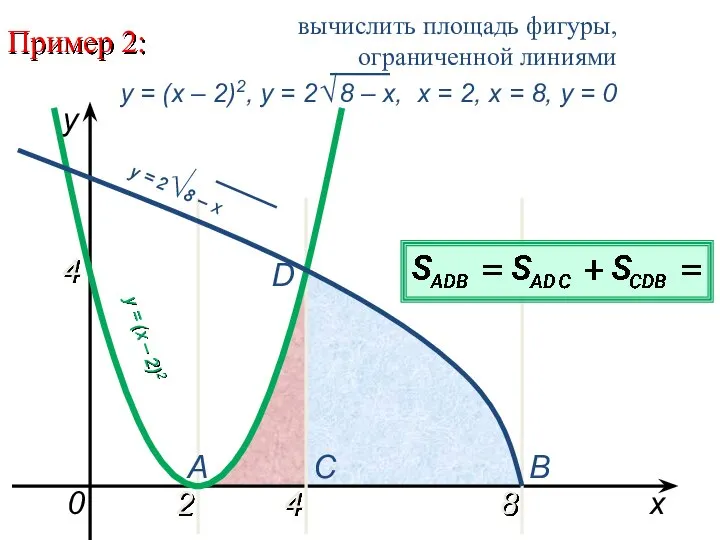
Слайд 8Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y
4
Слайд 11Таблица первообразных
f(x)
F(x)
F(x)









 Автор: С.А.Данилова учитель математики ГБОУСОШ№625 с углубленным изучением математики Невского района Санкт-Петербурга им. Героя Р
Автор: С.А.Данилова учитель математики ГБОУСОШ№625 с углубленным изучением математики Невского района Санкт-Петербурга им. Героя Р Величины и их измерение. Длина
Величины и их измерение. Длина Презентация на тему СИСТЕМА ПОДГОТОВКИ УЧАЩИХСЯ К ЕГЭ ПО МАТЕМАТИКЕ
Презентация на тему СИСТЕМА ПОДГОТОВКИ УЧАЩИХСЯ К ЕГЭ ПО МАТЕМАТИКЕ  Задачи на движение
Задачи на движение Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины
Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины Кусочная функция
Кусочная функция Задачи на построение сечений
Задачи на построение сечений Ментальная арифметика в г. Камень-на-Оби
Ментальная арифметика в г. Камень-на-Оби Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Поверхности второго порядка
Поверхности второго порядка Неопределенный интеграл
Неопределенный интеграл Перпендикуляр и наклонная
Перпендикуляр и наклонная Математики Франции
Математики Франции Решение систем неравенств
Решение систем неравенств 7 класс
7 класс Урок по алгебре и началам анализа. Форма проведения - деловая игра Выборы!
Урок по алгебре и началам анализа. Форма проведения - деловая игра Выборы! Килограмм. Цепочка
Килограмм. Цепочка Квадратные уравнения
Квадратные уравнения Найдите наименьшее (наибольшее) значение функции на промежутке
Найдите наименьшее (наибольшее) значение функции на промежутке Решение задач с помощью уравнений
Решение задач с помощью уравнений Целые числа. Рациональные числа
Целые числа. Рациональные числа Векторы. Нулевой вектор
Векторы. Нулевой вектор Знакопостоянные ряды. Лекция 3.5
Знакопостоянные ряды. Лекция 3.5 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Знаки сравнения и знак равенства
Знаки сравнения и знак равенства Решение неравенств
Решение неравенств Старинные задачи с использованием дробей
Старинные задачи с использованием дробей