Содержание
- 2. Равенства, которые выполняются при определенных значениях переменной (переменных), называются уравнениями. 3х – 1 = 5; х2
- 3. Линейным уравнением с одной переменной х называют уравнение вида kx + b = 0, где k
- 4. Для решения линейных уравнений надо: Слагаемые, зависящие от х, перенести в одну часть уравнения, числа –
- 6. Равенство, содержащее две переменные, называют уравнением с двумя переменными (или неизвестными). Если в уравнение неизвестные входят
- 7. Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений,
- 8. Система двух линейных уравнений с двумя неизвестными имеет вид:
- 9. Способы решения систем двух линейных уравнений с двумя неизвестными: графический способ; способ подстановки; способ сложения.
- 12. Скачать презентацию









 Степенная функция (занятия 1, 2, 3)
Степенная функция (занятия 1, 2, 3) Правильные многогранники
Правильные многогранники Контрольная работа по математике. Двузначные числа
Контрольная работа по математике. Двузначные числа Страна геометрических фигур
Страна геометрических фигур Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Условный оператор задач
Условный оператор задач Последовательности. Предел последовательности. Отображение
Последовательности. Предел последовательности. Отображение Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников Арифметическая прогрессия
Арифметическая прогрессия Выполни цепочку
Выполни цепочку Прямая и плоскость
Прямая и плоскость Единицы, десятки
Единицы, десятки Ряды распределения в статистике
Ряды распределения в статистике Правоотношения и субъекты права. 9 класс
Правоотношения и субъекты права. 9 класс Решение уравнений и неравенств. Линейные уравнения и неравенства
Решение уравнений и неравенств. Линейные уравнения и неравенства Приведение к каноническому виду центральных линий второго порядка
Приведение к каноническому виду центральных линий второго порядка Решение логарифмических уравнений
Решение логарифмических уравнений Занятие 01.10+Задания для п.р
Занятие 01.10+Задания для п.р Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Уравнение прямой
Уравнение прямой Задачи на построение и этапы их решения
Задачи на построение и этапы их решения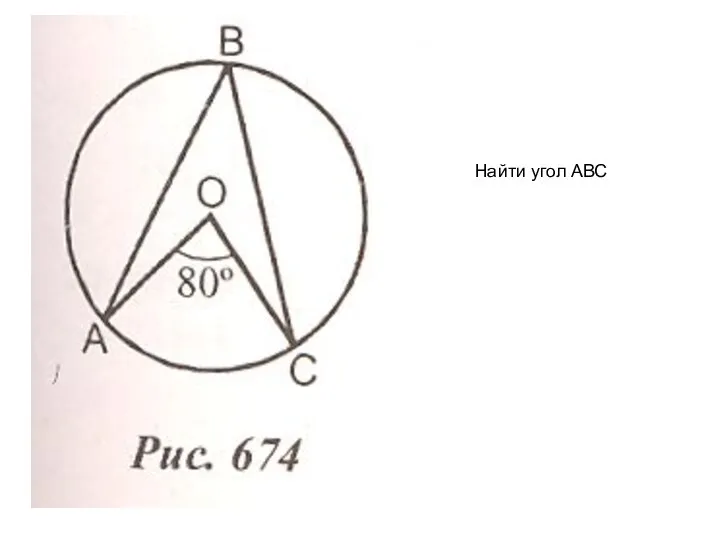 Найти угол АВС
Найти угол АВС Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК
Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК Средняя скорость движения. Задание по графикам
Средняя скорость движения. Задание по графикам Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Производная по направлению. Градиент и его свойства
Производная по направлению. Градиент и его свойства Математика в медицине
Математика в медицине Понятие математической индукции и ее применение
Понятие математической индукции и ее применение