Содержание
- 2. Логарифмические неравенства - Если основание логарифма больше 1, то знак неравенства сохраняется, если основание логарифма меньше
- 3. Логарифмические неравенства - неравенства, содержащие логарифмические функции.
- 4. Логарифмические неравенства - ОДЗ логарифмического выражения достаточно проверить только для меньшего из двух логарифмических выражений. Полезно
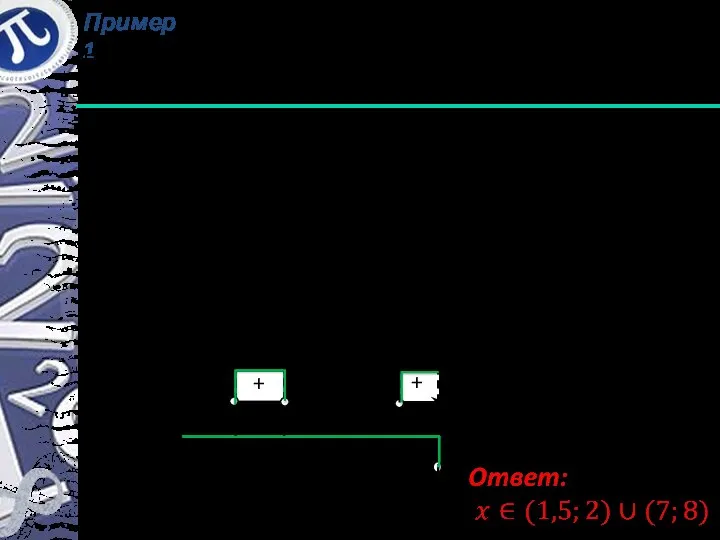
- 5. Пример 1 Решить неравенство Решение:
- 6. Пример 1 Решить неравенство + - + -
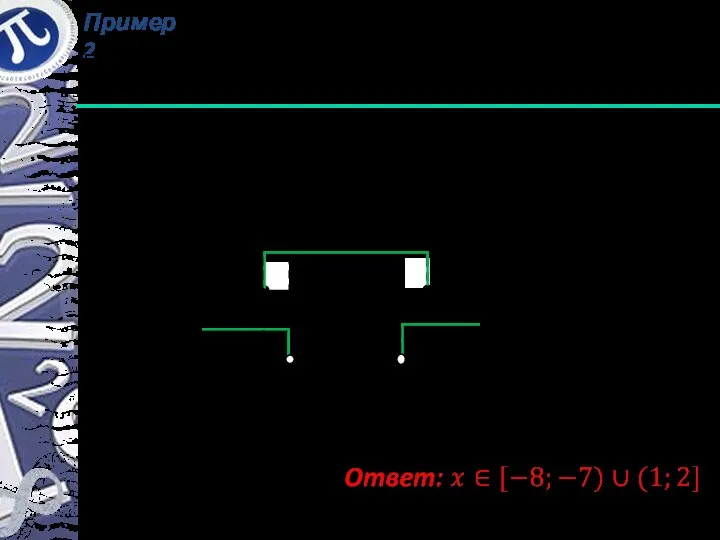
- 7. Пример 2 Решить неравенство Решение:
- 8. Пример 2 Решить неравенство + - + + - +
- 9. Неравенство вида
- 10. Обобщим - Неравенство вида Где ∨ - любой из знаков неравенства: ; ≤; ≥.
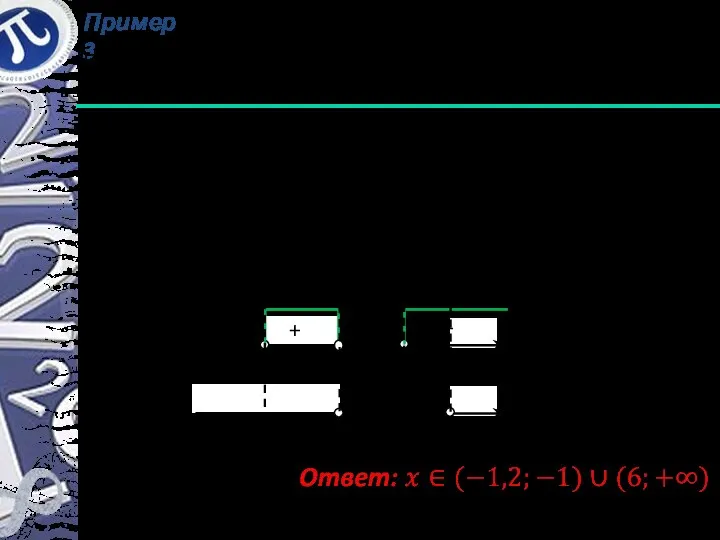
- 11. Пример 3 Решить неравенство Решение: Найдём ОДЗ: + - + 1 0
- 12. Пример 3 Решить неравенство Теперь запишем систему вида В нашем случае Далее решим второе неравенство полученной
- 13. Пример 3 Решить неравенство Итак, + - + -1 - -1
- 14. Обобщим - Неравенство вида Где ∨ - любой из знаков неравенства: ; ≤; ≥.
- 15. Неравенство вида Где ∨ - любой из знаков неравенства: ; ≤; ≥.
- 16. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства Решение: Найдём ОДЗ: на промежутке [0;21].
- 17. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21]. Заметим, что 121=112
- 18. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21]. Воспользуемся правилом В
- 19. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21]. Решим второе неравенство
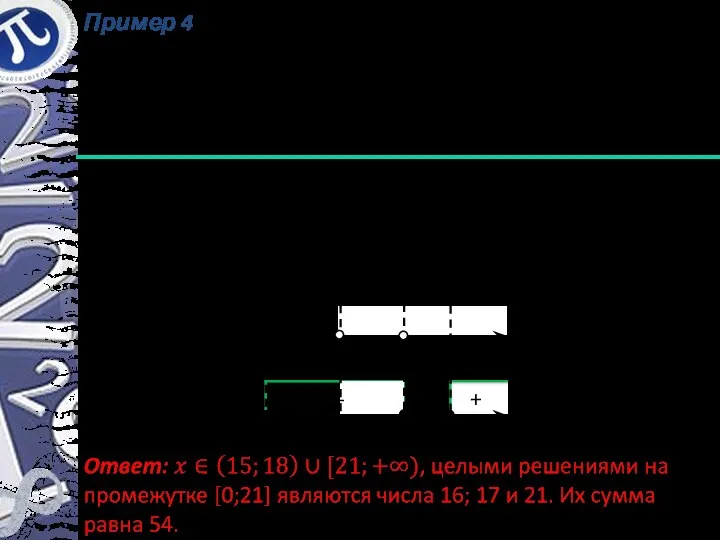
- 20. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21].
- 21. Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21]. В итоге получаем
- 22. Для всех других неравенств перед их решением ОБЯЗАТЕЛЬНО нужно указать ОДЗ переменной: Основание логарифма больше 0
- 24. Скачать презентацию










![Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства Решение: Найдём ОДЗ: на промежутке [0;21].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/991532/slide-15.jpg)



![Пример 4 (ЦТ 2008 В9) Найдите сумму целых решений неравенства на промежутке [0;21].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/991532/slide-19.jpg)

 Симплексный метод
Симплексный метод Координаты на прямой
Координаты на прямой Что будет со мной, если буду питаться, как Дюймовочка?
Что будет со мной, если буду питаться, как Дюймовочка? Таблица умножения трёх
Таблица умножения трёх Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение  Действия с рациональными числами. Урок-игра Полёт в космос
Действия с рациональными числами. Урок-игра Полёт в космос Математика в биологии
Математика в биологии Численные методы. ВСР 3
Численные методы. ВСР 3 Единицы измерения, их история
Единицы измерения, их история Решение систем линейных неравенств
Решение систем линейных неравенств Презентация на тему Четные и нечетные функции
Презентация на тему Четные и нечетные функции  Статистическая обработка данных в механике. Комбинаторика, теория вероятности
Статистическая обработка данных в механике. Комбинаторика, теория вероятности Логические схемы
Логические схемы Памятки по математике
Памятки по математике Постройте сечения, проходящие через точки K, L, M
Постройте сечения, проходящие через точки K, L, M урок 1, урок 2 9кл геом водный урок
урок 1, урок 2 9кл геом водный урок Устный счёт
Устный счёт Площадь на клетке
Площадь на клетке Танграм (древняя китайская головоломка)
Танграм (древняя китайская головоломка) Режим поступления заявок
Режим поступления заявок Разряды чисел
Разряды чисел Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Римские цифры
Римские цифры Дискретные случайные величины
Дискретные случайные величины Концентрические замощения на основе ромбов Пенроуза
Концентрические замощения на основе ромбов Пенроуза Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Исследование функций
Исследование функций