Содержание
- 2. План лекции Классификация моделей, прямая и обратная задачи, виды моделирования. Процесс моделирования, критерий выбора. Стандартные постановки
- 3. Математическая модель Математическая модель – математическое представление реальности, один из вариантов модели, как системы, исследование которой
- 4. Классификация моделей
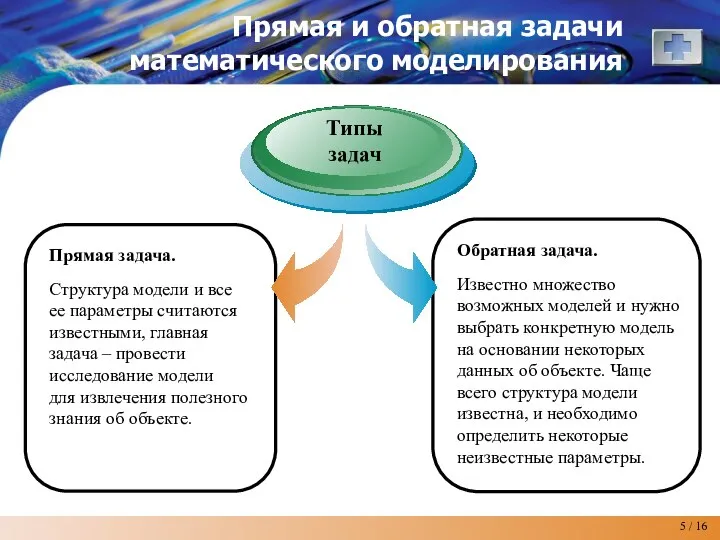
- 5. Прямая и обратная задачи математического моделирования Прямая задача. Структура модели и все ее параметры считаются известными,
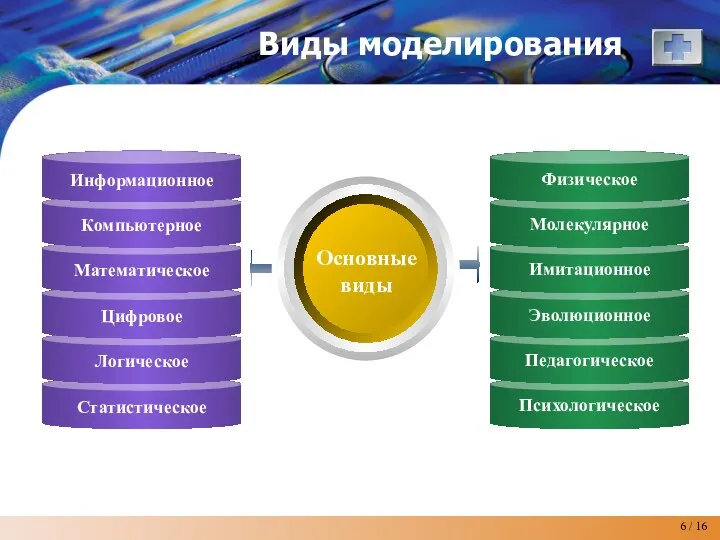
- 6. Виды моделирования
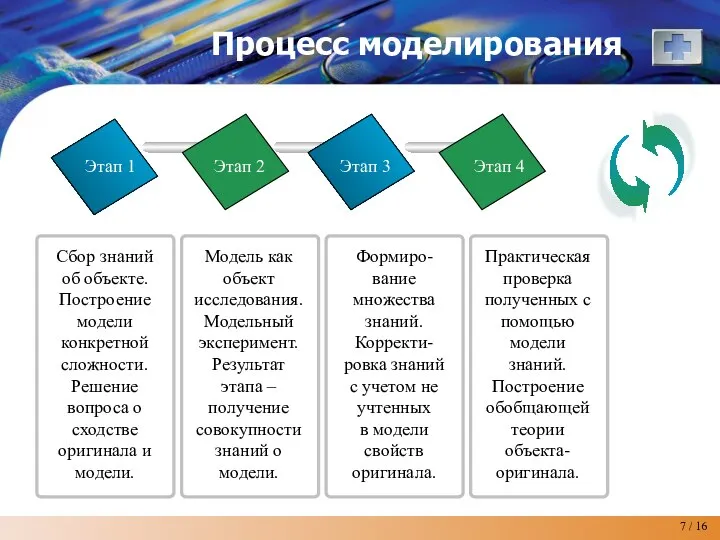
- 7. Процесс моделирования Этап 1 Этап 2 Этап 3 Этап 4 Сбор знаний об объекте. Построение модели
- 8. Критерии выбора моделей и методы отбора признаков Внешние критерии: адекватность, непротиворечивость, полнота, точность, универсальность Внутренние критерии:
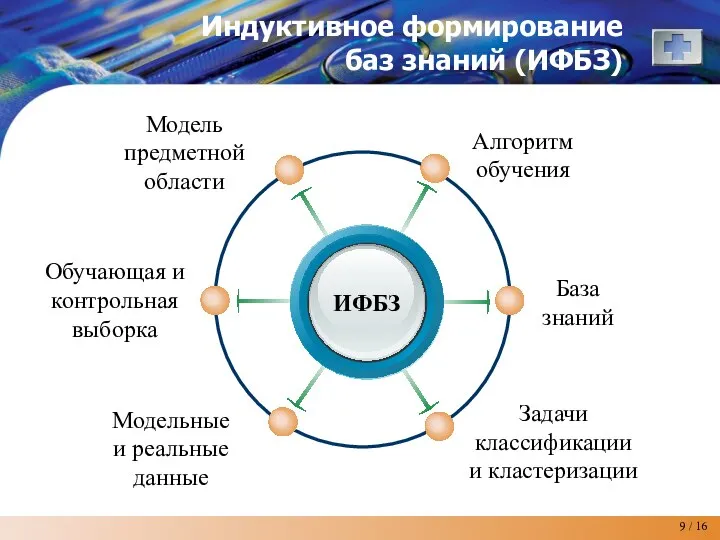
- 9. ИФБЗ Алгоритм обучения Модель предметной области База знаний Задачи классификации и кластеризации Обучающая и контрольная выборка
- 10. Стандартные постановки основных задач ИФБЗ Для некоторого множества моделей зависимости, к которому относится неизвестная зависимость между
- 11. Правильная и точная классификации Правильная классификация – если одним из классов объекта, выдаваемых решающим правилом, является
- 12. Отличия задач классификации и кластеризации Задача кластеризации отличается от задачи классификации тем, что в первом случае
- 13. Компоненты формирования Индуктивная база знаний формирование Обучающая выборка Алгоритм обучения Постановка задачи Модель
- 14. Алгоритм обучения классификации Алгоритм классификации (алгоритм обучения классификации) – это отображение, которое по обучающей выборке строит
- 15. Пусть имеются алгоритмы классификации , для моделей соответственно, и обучающая выборка t. Для модели m требуется
- 17. Скачать презентацию










 Математический анализ. Производная и первообразная
Математический анализ. Производная и первообразная Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Понятие функции и ее графика
Понятие функции и ее графика Многоугольники. Виды многоугольников
Многоугольники. Виды многоугольников Перпендикулярные прямые
Перпендикулярные прямые Формулы двойного угла
Формулы двойного угла Справочник по геометрии
Справочник по геометрии Решение задач с помощью теоремы Пифагора
Решение задач с помощью теоремы Пифагора Прямоугольник, ромб, квадрат. Решение задач
Прямоугольник, ромб, квадрат. Решение задач Задачи на составление уравнений. 7 класс
Задачи на составление уравнений. 7 класс Функция y=k/x, её график и свойства. 8 класс. Урок 3
Функция y=k/x, её график и свойства. 8 класс. Урок 3 Многоугольники
Многоугольники Определение перемещения
Определение перемещения Числовая последовательность
Числовая последовательность Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Ответы для самопроверки
Ответы для самопроверки Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ Умножение десятичных дробей
Умножение десятичных дробей Центральная симметрия
Центральная симметрия Таблица сложения
Таблица сложения Геометричне моделювання організаційних кластерних сруктур
Геометричне моделювання організаційних кластерних сруктур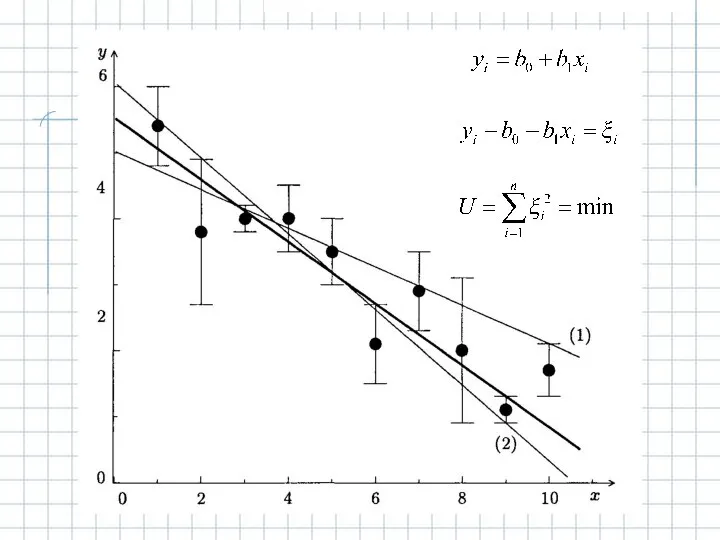 Расчет коэффициентов регрессии (МНК)
Расчет коэффициентов регрессии (МНК) Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса Объем куба. Задача
Объем куба. Задача Тригонометриялық функциялардың қос бұрышының және жарты бұрышының формулалары
Тригонометриялық функциялардың қос бұрышының және жарты бұрышының формулалары Понятие вектора. Векторы на плоскости
Понятие вектора. Векторы на плоскости Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)