Все способы решения тригонометрических уравнений

Тригонометрия и ее создатель
Тригономе́трия (от греч. τρίγωνον (треугольник) и греч. μέτρεο (меряю), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму земли).

Бартоломеус Питискус
Бартоломе́ус Пити́скус (или Бартоломео Питиск, нем. Bartholomäus Pitiscus, 1561—1613) — немецкий математик,астроном,
теолог-кальвинист. Внёс вклад в развитие тригонометрии, в том числе предложил сам термин «тригонометрия» в качестве названия этой науки.

Тригонометрические уравнения. Определение
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Простейшими тригонометрическими уравнениями являются уравнения вида.

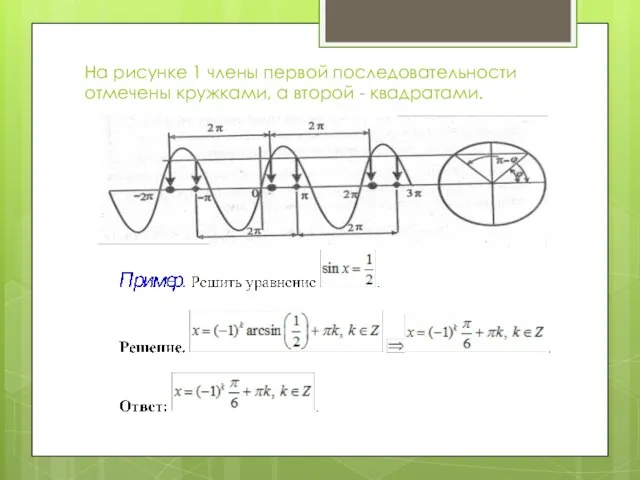
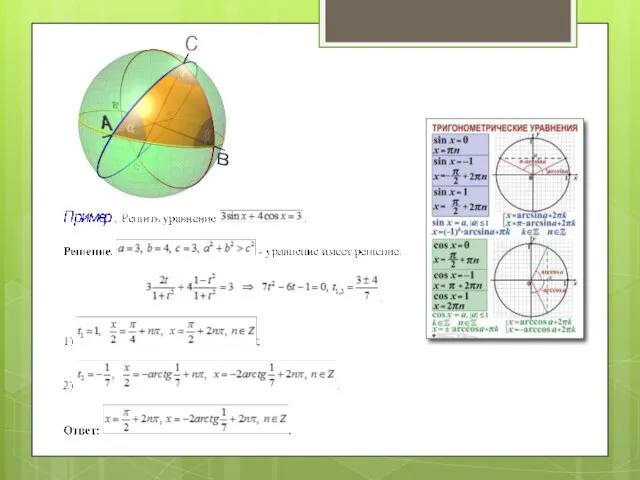
Уравнение SIN X=a

На рисунке 1 члены первой последовательности отмечены кружками, а второй - квадратами.

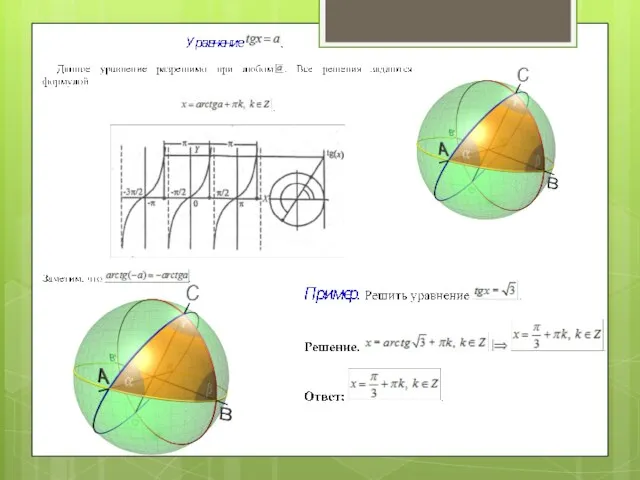
Основные методы решения
Любое тригонометрическое уравнение в процессе решения с помощью надлежащих преобразований должно быть приведено к простейшим. Наиболее часто при решении тригонометрических уравнений применяются следующие методы:
разложение на множители;
способ замены (сведение к алгебраическим уравнениям);
сведение к уравнениям, однородным относительно и ;
преобразование суммы тригонометрических функций в произведение;
преобразование произведения тригонометрических функций в сумму;
использование формул понижения степени;
равенство одноименных тригонометрических функций;
равенство одноименных тригонометрических функций
введение вспомогательного аргумента.

Способ замены
При решении уравнений этим методом необходимо знать формулы:

Однородные уравнения

Разложение на множители

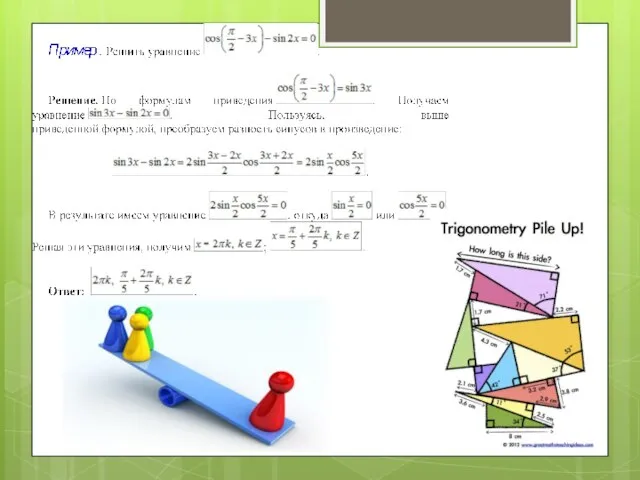
Преобразование суммы тригонометрических функций в произведение
При решение уравнений данным способом необходимо знать формулы:

Преобразование произведения тригонометрических функций в сумму
При решение уравнений данным способом необходимо знать формулы:

Использование формул понижения степени

Равенство одноименных тригонометрических функций

Введение вспомогательного аргумента

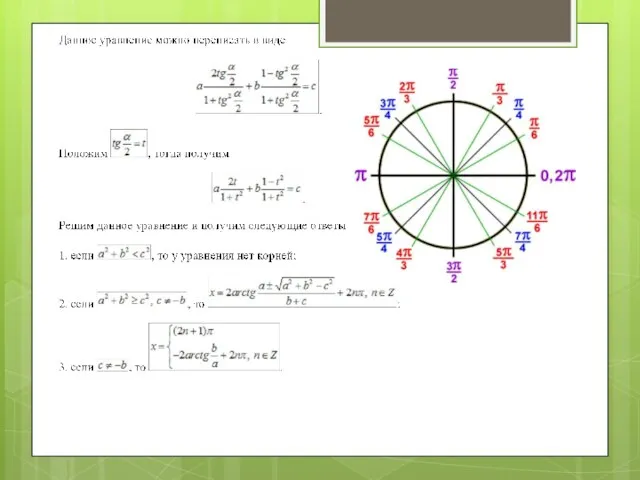
Метод рационализации для уравнения вида

Приведение к однородному для уравнения вида

Подведем итоги!
Долгое время тригонометрия носила чисто геометрический характер, т. е. факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.