Содержание
- 2. Первообразная Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из
- 3. Основное свойство первообразных Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C –
- 4. Неопределенный интеграл Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается : ,
- 5. Правила интегрирования
- 6. Определенный интеграл В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a
- 7. Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные
- 8. Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница) Для непрерывной функции где F(x) –
- 9. Основные свойства определенного интеграла
- 10. Основные свойства определенного интеграла
- 11. Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x),
- 12. Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x),
- 13. Геометрический смысл определенного интеграла Замечание: Если функция изменяет знак на промежутке [a;b] , то
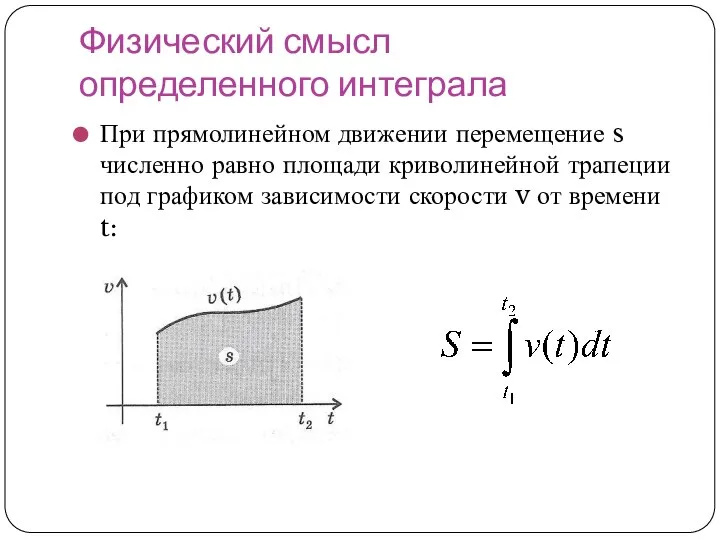
- 14. Физический смысл определенного интеграла При прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком
- 15. с помощью определенного интеграла Вычисление площадей и объемов
- 16. Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b],
- 18. Скачать презентацию





![Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1113031/slide-6.jpg)





![Геометрический смысл определенного интеграла Замечание: Если функция изменяет знак на промежутке [a;b] , то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1113031/slide-12.jpg)


 Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Представляют геометрические фигуры
Представляют геометрические фигуры Матрицы. 1 часть
Матрицы. 1 часть Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Случаи сложения вида +5
Случаи сложения вида +5 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Формула Пика
Формула Пика Перпендикулярность плоскостей
Перпендикулярность плоскостей Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов
Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах
П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса
Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса Задания с фигурами
Задания с фигурами Алгебра в жизни человека
Алгебра в жизни человека Презентация на тему Арифметическая прогрессия: практикум
Презентация на тему Арифметическая прогрессия: практикум 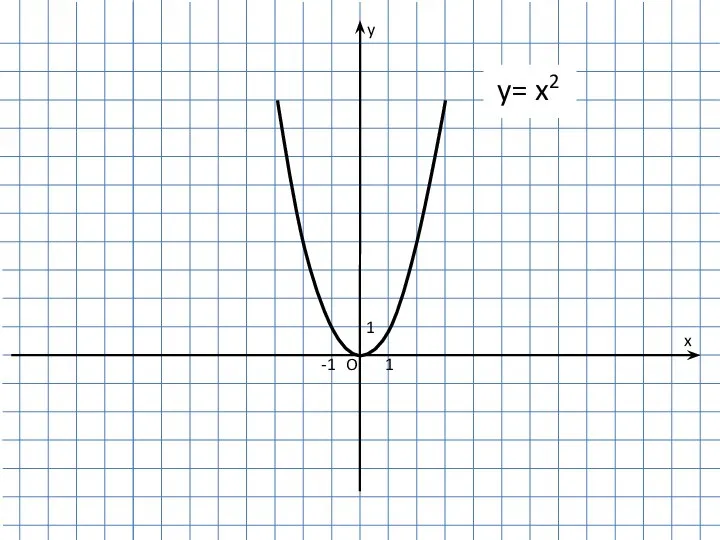 Функция y= x2
Функция y= x2 Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Неравенство треугольника (7 класс)
Неравенство треугольника (7 класс) Формулы сокращенного умножения. Космический час на планете знаний
Формулы сокращенного умножения. Космический час на планете знаний Теория множеств
Теория множеств Многоугольники
Многоугольники Уравнение линии на плоскости
Уравнение линии на плоскости Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Прибавить и вычесть число 1
Прибавить и вычесть число 1 Площади и объемы многогранников. Решение задач
Площади и объемы многогранников. Решение задач