Слайд 2
LECTURE 9
MATRIX ALGEBRA AND SIMULTANEOUS LINEAR EQUATIONS
Temur Makhkamov
Indira Khadjieva
QM Module Leader

Слайд 3Lecture outline
The meaning and properties of matrices;
The arithmetic operations on matrices;
The applications

of matrices to reality
Слайд 4Matrix
A Matrix is simply a rectangular array of numbers arranged in rows

and columns.
The size of a matrix is indicated by the number of its rows and the number of its columns
The whole matrix is labeled by a capital letter
The individual numbers (elements) contained in the matrix are labeled by lower case letters with a suffix to identify their locations within the matrix.
Слайд 5Examples of matrices
Examples:
1) – 2x2 matrix
2) – 2x3 matrix
3) – ?

Слайд 6Addition (and Subtraction) of matrices
You can add (subtract) two matrices of

the same size (equal number of rows and columns).
The sum (difference) of two equal-sized matrices results in the new matrix of the same size as the two matrices being added.
Example:
Слайд 7Exercise: Addition and Subtraction

Слайд 8Scalar multiplication
Multiply each element of the matrix by the number.
Example:

Слайд 9Exercise: Scalar multiplication

Слайд 10Matrix multiplication
Two matrices can be multiplied only if the number of columns

of the 1st matrix equals to the number of the rows of the 2nd matrix.
Multiply rows of the 1st matrix by columns of the 2nd matrix
Example:
Слайд 11Matrix Transpose
The transpose of matrix can be obtained by interchanging the rows

and columns
The first row of the matrix A is the first column of matrix A transposed
Слайд 12Zero & Identity matrix
Zero matrix is a matrix with all elements 0.
Identity

matrix is a square matrix with elements of 1s on the main diagonal from top left to bottom right and 0s on other positions
Слайд 13Determinant of a matrix
A numerical value of matrix
Can be a negative number
Exists

for a square matrix only
Determinant for 2x2 matrix is calculated as follows:
Слайд 14Inverse of a (2x2) matrix (1)
If then

Слайд 15Inverse of a (2x2) matrix (2)
Example: , then
Calculate:
Check:

























 Тетраэдр и параллелепипед
Тетраэдр и параллелепипед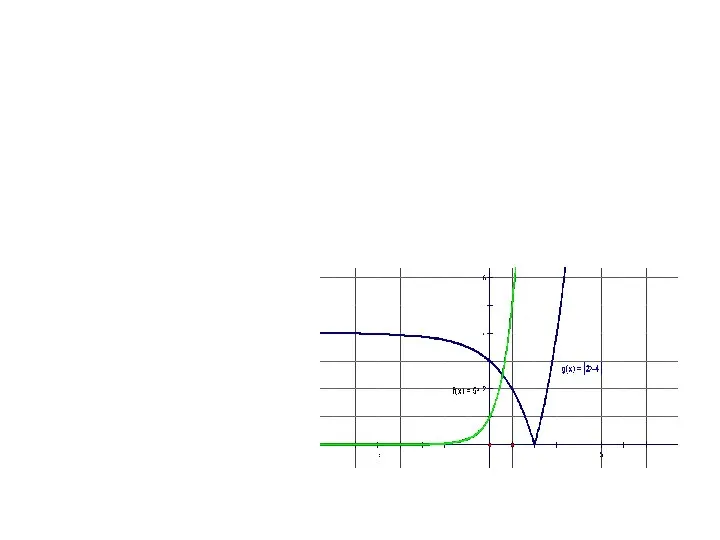 Показательные уравнения
Показательные уравнения Что? Где? Когда?
Что? Где? Когда? Формы работы при подготовке к ЕГЭ
Формы работы при подготовке к ЕГЭ Работа над ошибками
Работа над ошибками Функции y=x2 и y=x3 и их графики
Функции y=x2 и y=x3 и их графики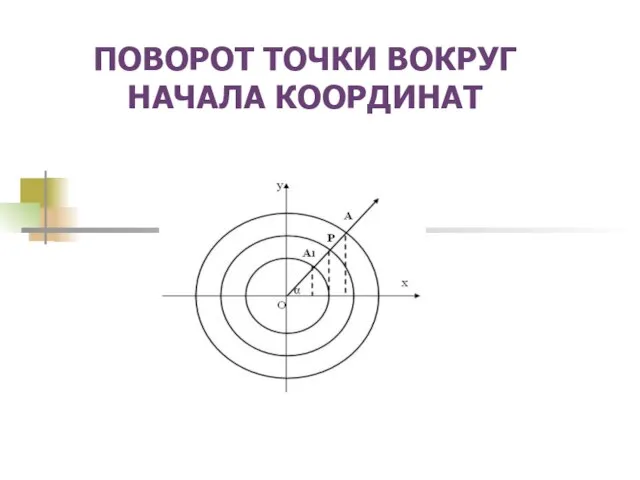 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Теорема Пифагора и способы ее доказательства
Теорема Пифагора и способы ее доказательства Показательные неравенства
Показательные неравенства Решение задач на доказательство равенства треугольников на готовых чертежах
Решение задач на доказательство равенства треугольников на готовых чертежах Повторение изученного. 1 класс
Повторение изученного. 1 класс Презентация на тему Устный счет на уроках математики
Презентация на тему Устный счет на уроках математики  Изучение таблицы деления
Изучение таблицы деления Умножение обыкновенных дробей
Умножение обыкновенных дробей Многогранники и их основные свойства
Многогранники и их основные свойства Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva Площадь треугольника
Площадь треугольника Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Порядок выполнения действий. Скобки
Порядок выполнения действий. Скобки Пирамида. Решение задач
Пирамида. Решение задач Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Производная. Определение производной, ее геометрический и физический смысл
Производная. Определение производной, ее геометрический и физический смысл Glava_5_-_Proektirovanie_vyborki_Gubko_A_M
Glava_5_-_Proektirovanie_vyborki_Gubko_A_M Построения циркулем и линейкой
Построения циркулем и линейкой Презентация на тему Связь между слагаемыми и суммой
Презентация на тему Связь между слагаемыми и суммой  Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Теория Пределов
Теория Пределов